系统学习机器学习之线性判别式（一）

最新推荐文章于 2021-01-21 22:36:03 发布

Eason.wxd

最新推荐文章于 2021-01-21 22:36:03 发布

阅读量6.9k

点赞数

分类专栏：机器学习

本文链接：https://blog.csdn.net/App_12062011/article/details/50357669

版权

机器学习专栏收录该内容

83 篇文章 40 订阅

订阅专栏

基础的线性判别式，这里不做说明。主要是逻辑斯蒂判别式的说明和梯度下降迭代求解算法。

1.逻辑斯蒂方程（Logistic Equation）

逻辑斯蒂方程的推导

　　当一种新产品刚面世时，厂家和商家总是采取各种措施促进销售。他们都希望对这种产品的推销速度做到心中有数，这样厂家便于组织生产，商家便于安排进货。怎样建立数学模型描述新产品推销速度呢？

　　首先要考虑社会的需求量．社会对产品的需求状况一般依如下两个特性确定：

　　1. 对产品的需求有一个饱和水平．当产品需求量达到一定数量时，对这种产品的需求也饱和了，设饱和水平为a；

　　2. 假设在时刻t，社会对产品的需求量为x=x(t)，需求的增长速度dx/dt正比于需求量x(t)与需求接近饱和水平的程度a-x(t)之乘积，记比例系数为k ；

　　根据上述实际背景的两个特征，可建立如下微分方程：

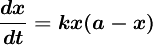　　 $\boldsymbol{\frac{dx}{dt}=kx(a-x)}$ .......................(1)

　　分离变量，得:

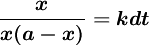
　　 $\boldsymbol{\frac{x}{x(a-x)}=kdt}$

　　两边积分，得:

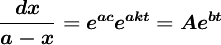
　　 $\boldsymbol{\frac{dx}{a-x}=e^{ac}e^{akt}=Ae^{bt}}$

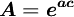
　　其中: $\boldsymbol{A=e^{ac}}$

　　从而，通解为:

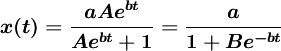　　 $\boldsymbol{x(t)=\frac{aAe^{bt}}{Ae^{bt}+1}=\frac{a}{1+Be^{-bt}}}$ ......(2)

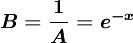　　其中 $\boldsymbol{B=\frac{1}{A}=e^{-x}}$ ，B和b为正常数，可由初始条件确定。式(1)称为逻辑斯蒂方程(1ogistic equation)，式(2)称为逻辑斯蒂曲线。

逻辑斯蒂方程的基本性质

　　1.当t=O时，x(t)的值为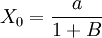： $X_0=\frac{a}{1+B}$ ；

　　2.x(t)的增长率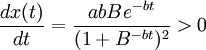 $\frac{dx(t)}{dt}=\frac{abBe^{-bt}}{(1+B^{-bt})^2}>0$ ,因此，x(t)是增函数；

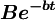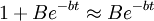　　3.当B值较大而t较小时， $\boldsymbol{Be^{-bt}}$ 将很大， $1+Be^{-bt} \approx Be^{-bt}$ ,于是

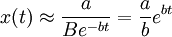
　　 $x(t) \approx \frac{a}{Be^{-bt}}=\frac{a}{b}e^{bt}$

　　x(t)近似于依指数函数增大，销售速度不断增大；

　　4.当t增大以后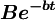， $\boldsymbol{Be^{-bt}}$ 越来越接近于零，分母越来越接近于1，销售速度开始下降，x(t)的值接近于a（饱和值）。

逻辑斯蒂方程的应用

　　1．人口限制增长问题

　　人口的增长不是呈指数型增长的，这是由于环境的限制、有限的资源和人为的影响，最终人口的增长将减慢下来。实际上，人口增长规律满足逻辑斯蒂方程。

　　2. 信息传播问题

　　所谓信息传播可以是一则新闻，一条谣言或市场上某种新商品有关的知识,在初期，知道这一信息的人很少，但是随时间的推移，知道的人越来越多，到一定时间，社会上大部分人都知道了这一信息．这里的数量关系可以用逻辑斯蒂方程来描述。若以t表示从信息产生算起的时间，P表示已知信息的人口比例，则逻辑斯蒂方程变为：

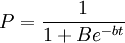　　 $P=\frac{1}{1+Be^{-bt}}$ ...................(3)

　　例如,当某种商品调价的通知下达时，有10％的市民听到这一通知，2小时以后，25％的市民知道了这一信息，由逻辑斯蒂方程可算出有75％的市民了解这一情况所需要的时间。

　　在方程(3)中，由t=0时，P=10％可得 B＝9;再由t=2时，P=25％可得,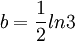 $b=\frac{1}{2}ln3$ 。

　　当P=75％时，有:

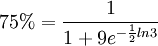
　　 $75%=\frac{1}{1+9e^{-\frac{1}{2}ln3}}$

　　解得t=6，即6小时后，全市有75％的人了解这一通知。

　　3.商品销售预测问题

　　例如，某种商品的销售，开始时，知道的人很少，销售量也很小。当这种商品信息传播出去后，销售量大量增加，到接近饱和时销售量增加极为缓慢。比如，这种商品饱和量估计a=500(百万件)，大约5年可达饱和，常数b经测定为b=lnl0，B=100。下面我们来预测一下第3年末的销售量是多少。

　　由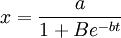 $x=\frac{a}{1+Be^{-bt}}$ ,有:

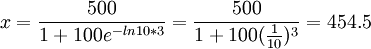　　 $x=\frac{500}{1+100e^{-ln10*3}}=\frac{500}{1+100(\frac{1}{10})^3}=454.5$ (百万件)

　　所以第三年末的市场销售量大约为454.5百万件，这样可以做到有计划地生产。

　　逻辑斯蒂方程的应用比较广泛。如果问题的基本数量特征是：在时间t很小时，呈指数型增长，而当t增大时，增长速度就下降，且越来越接近于一个确定的值，这类问题可以用逻辑斯蒂方程加以解决。

逻辑斯蒂方程案例分析

案例一：基于逻辑斯蒂方程的垃圾邮件过滤特征方法的研究^[1]

　　1.逻辑斯蒂(Logistic)方程

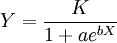　　 $Y=\frac{K}{1+ae^{bX}}$ (1)

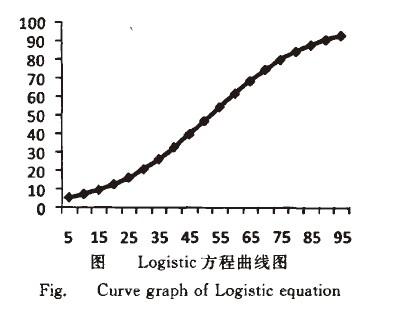
　　Logistic曲线其特点是开始增长缓慢，而在以后的某一范围内迅速增长，达到某限度后，增长又缓慢下来∞3.曲线略呈拉长的“S”型.Logistic增长的速度函数图像为单峰曲线，这表明Logistic曲线增长过程分为三个阶段：慢一快一慢。

　　在实际中，特征项也根据重要程度的不同分为三部分，并且与Logistic曲线的三个阶段相对应：第一部分是在垃圾邮件分类中贡献甚微的特征项，特征权值不需要明显的变化，全部是不予选择的特征项，对应Logistic曲线变化幅度较小的第一阶段；第二部分是要进行甄别的特征项，需要区别特征项重要程度强弱，特征权值变化幅度越大越有利于特征项的选择，与曲线的变化幅度最快的第二阶段对应；第三个部分是必须选取的高特征权值的特征项，对应曲线第三阶段，这部分特征项同样不需要显著的差别，全部是要选择的特征项.2.参数设定。

　　2.参数设定

　　以影响特征选择方法的三个要素为因子，设逻辑斯蒂(Logistic)方程的参数X为：

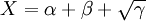　　 $X=\alpha+\beta+\sqrt{\gamma}$ (2)

　　根据(8)式测定垃圾邮件中特征项集的X值分布情况：P(X<100)>90％，即特征权值小于100的特征项占待选择特征项集的95％以上，可判定需要甄别的特征项集中在X值小于lOO的特征项集合内，由此设定一组样本值(X_1,Y_1),(X_2,Y_2),\cdots(\cdotsX_10,Y_10),，其数值如下表所示.以此分析此结果是否能以Logistic方程描述。

　　表：X，Y参数值表

X	10	20	30	40	50	60	70	80	90	95
y	9	12	16	30	50	65	77	84	90	93

　　在(1)式中，当X→∞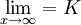， $\lim_{x \to \infty}=K$ ，所以特征项重要程度的无限延长的终极量是K.假定这组值的K值为100(％)，即特征项的最重要程度为100％.将(1)式移项得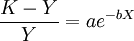： $\frac{K-Y}{Y}=ae^{-bX}$ (3)

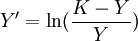　　令 $Y^\prime=\ln(\frac{K-Y}{Y})$ ,则由最小平方法估计的 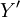$Y^\prime$ 为

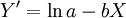　　 $Y^\prime=\ln a-bX$ (4)

　　因此，Y和X对于Logistic方程的符合度，可由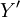 $Y^\prime$ 和X的线性相关系数 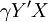$\gamma Y^\prime X$ 给出：

　　 $\gamma Y^\prime X=\frac{\sum XY^\prime-\frac{1}{n}(\sum X)(\sum Y^\prime)}{\sqrt{\left[\sum X^2-\frac{1}{n}(\sum X^2)\right]\left[\sum(Y^\prime)^2-\frac{1}{n}(\sum Y^\prime)^2\right]}}=\frac{\sum xy^\prime}{\sqrt{\sum X^2\cdot\sum(y^\prime)^2}}$ (5)

　　(5)中，

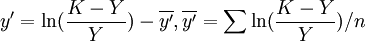　　 $y^\prime=\ln(\frac{K-Y}{Y})-\overline{y^\prime},\overline{y^\prime}=\sum\ln(\frac{K-Y}{Y})/n$ (6)

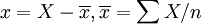　　 $x=X-\overline{x},\overline{x}=\sum X/n$ (7)

　　以为样本容量。回归参数a和b的样本估计值为：

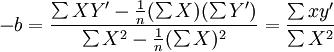　　 $-b=\frac{\sum XY^\prime-\frac{1}{n}(\sum X)(\sum Y^\prime)}{\sum X^2-\frac{1}{n}(\sum X)^2}=\frac{\sum xy^\prime}{\sum X^2}$ (8)

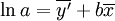　　 $\ln a=\overline{y^\prime}+b\overline{x}$ (9)

　　根据表2以及式(6)(7)求得：

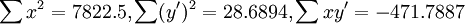
　　 $\sum x^2=7822.5,\sum(y^\prime)^2=28.6894,\sum xy^\prime=-471.7887$

　　故根据(11)得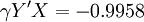： $\gamma Y^\prime X=-0.9958$ 为极显著.故知X和Y的关系以Logistic方程配合是合适的.进一步根据(6)和(7)求得b值为0.0603和a值为23.1316.那么所求Logistic方程为：

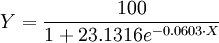
　　 $Y=\frac{100}{1+23.1316e^{-0.0603\cdot X}}$

　　式（10）的曲线图如图所示

　　3.实验和结果

　　采用的是CCERT的中文邮件样本集，该样本集由中国教育科研网收集并维护．该数据集在国内和教育网内是常用的一个衡量反中文垃圾邮件技术的数据集．采用数据集的8000封垃圾邮件以及8000封正常邮件．选择贝叶斯方法进行垃圾邮件分类，分类结果利用查全率(Recall)、准确率(Precision)和F值评测过滤系统性能。

　　查全率(R)=正确过滤掉的邮件数／应该过滤掉的垃圾邮件数；

　　准确率(P)=正确过滤掉的邮件数／实际过滤掉的邮件数；

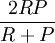　　 $\frac{2RP}{R+P}$ ；值实际是查全率和准确率的调和平均，综合成一个指标．实验结果如下表。

　　表：统评测结果

信息熵	互信息	几率比	期望交叉熵	CHI统计量	Logistic方程
Recall	0.8446	0.8615	0.8954	0.8702	0.8737	0.9366
Precision	0.9698	0.9574	0.9421	0.9363	0.9316	0.9493
F	0.9028	0.9037	0.9181	0.9020	0.9017	0.9429

　　实验结果表明，利用Logistic方程进行分类时的F值有显著的提高，说明过滤系统整体性能有所提高，其中查全率有明显的提高，说明这种方法检出垃圾邮件的能力较高，使漏网的垃圾邮件减少，但是准确率没有提升，说明合法邮件误判为垃圾邮件的可能性没有明显降低。

梯度下降法(gradient descent)是一个最优化算法，通常也称为 最速下降法。实际上，还有牛顿法最优化算法。

常用于机器学习和人工智能当中用来递归性地逼近最小偏差模型。

求解过程

顾名思义，梯度下降法的计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）。

其迭代公式为

,其中

代表梯度负方向，

表示梯度方向上的搜索步长。梯度方向我们可以通过对函数求导得到，步长的确定比较麻烦，太大了的话可能会发散，太小收敛速度又太慢。一般确定步长的方法是由线性搜索算法来确定，即把下一个点的坐标a _k+1看做是的函数，然后求满足f(a _k+1)的最小值的即可。

因为一般情况下，梯度向量为0的话说明是到了一个极值点，此时梯度的幅值也为0.而采用梯度下降算法进行最优化求解时，算法迭代的终止条件是梯度向量的幅值接近0即可，可以设置个非常小的常数阈值。

例子

举一个非常简单的例子，如求函数

的最小值。

利用梯度下降的方法解题步骤如下：

1、求梯度，

2、向梯度相反的方向移动

，如下

，其中，

为步长。如果步长足够小，则可以保证每一次迭代都在减小，但可能导致收敛太慢，如果步长太大，则不能保证每一次迭代都减少，也不能保证收敛。

3、循环迭代步骤2，直到

的值变化到使得

在两次迭代之间的差值足够小，比如0.00000001，也就是说，直到两次迭代计算出来的

基本没有变化，则说明此时

已经达到局部最小值了。

4、此时，输出

，这个

就是使得函数

最小时的

的取值。

MATLAB如下。

 
        syms x; 
       
        f=x^2; 
       
        step=0.1; 
       
        x=2; 
       
        loss_changed=x^2; 
       
        loss=x^2; 
       
        while  
        loss_changed>0.000000001 
       
        x=x-step*2*x; 
       
        loss_changed = loss - x^2; 
       
        loss = x^2 ; 
       
        end 
       
        x

梯度下降法处理一些复杂的非线性函数会出现问题，例如Rosenbrock函数：

其最小值在

处，函数值为

。但是此函数具有狭窄弯曲的山谷，最小点

就在这些山谷之中，并且谷底很平。优化过程是之字形的向极小值点靠近，速度非常缓慢。

Eason.wxd

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
系统学习机器学习之线性判别式（一）

基础的线性判别式，这里不做说明。主要是逻辑斯蒂判别式的说明和梯度下降迭代求解算法。1.逻辑斯蒂方程（Logistic Equation）逻辑斯蒂方程的推导　　当一种新产品刚面世时，厂家和商家总是采取各种措施促进销售。他们都希望对这种产品的推销速度做到心中有数，这样厂家便于组织生产，商家便于安排进货。怎样建立数学模型描述新产品推销速度呢？　　首先要考虑社会的需求量．社会对产品的需
复制链接

扫一扫