【深度学习入门】NNDL学习笔记（三）

Chapter 3 Improve the way neural networks learn

交叉熵损失函数 the cross-entropy cost function

1. We hope and expect that our neural networks will learn fast from their errors.

"learning is slow" is really the same as saying  are small. 

For x=1, y=0:                                  

The learning slows down when output is near 0 and 1, where σ' is small.

2.  The special function chosen to cancel the σ' (for a single neuron)：

binary entropy: -[yln(y)+(1-y)ln(1-y)].

Interpretation:

The first property: non-negative

The second property: If the neuron's actual output is close to the desired output for all training inputs, x, then the cross-entropy will be close to zero. To prove this I will need to assume that the desired outputs y are all either 0 or 1. This is usually the case when solving classification problems, for example, or when computing Boolean functions.

                                                             

                                                             

With sigmoid function σ, σ' = σ(1-σ)：

Then, the learning rate is controlled by the error.

Different cost functions should use different learning rates, ŋ. There's no meaning to compare ŋ among them. 

3. For multi-layer networks:

The cross-entropy is nearly always the better choice, provided the output neurons are sigmoid neurons.

4. cross-entropy: 

 

It's common to define the cross-entropy for two probability distributions, pj and qj , as .

Exercise:

The cross-entropy is small if σ(z)≈y for all training inputs. The argument relied on y being equal to either 0 or 1. This is usually true in classification problems, but for other problems (e.g., regression problems) y can sometimes take values intermediate between 0 and 1. Show that the cross-entropy is still minimized when σ(z)=y for all training inputs. When: 

Softmax (此部分写后忘记保存了，学完全书后再回来更新)

Overfitting and Regularization

1. Overfitting(overtraining): After some epochs, instead of decreasing, the cost fluctuates. And sometimess the accuracy stops increasing despite a small increase in cost function.

Early stopping: We can use a validation data set to prevent overfitting. Once the classification accuracy on the validation_data has saturated(not until we are confident that it's saturated), we stop training.

Hold out method -- A more generel strategy: To use the validation_data to evaluate different trial choices of hyper-parameters such as the number of epochs to train for, the learning rate, the best network architecture, and so on. Test dateset is only used for the final evaluations.

In fact, with a very large training test, it is difficult for even a very large network to overfit.

2. Regularization:

weight decay \ L2 regularization: add an extra term to the cost function, so the network prefer to learn small weights.

λ>0：regularization parameter; n: the size of the training set.

Learning rule: 

For weights, they are first rescaled by a factor, this is called weight decay.

With a mini-batch:

What's more, unregularized runs usually get 'stuck' as a result of local minima. But regularized runs are easier to produce replicable results.

The smallness of the weights means that the behaviour of the network won't change too much if we change a few random inputs here and there. That makes it difficult for a regularized network to learn the effects of local noise in the data.

3. Other techniques:

L1-regularization:

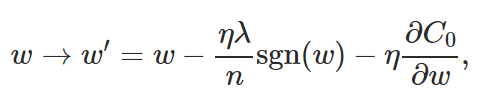
The net result is that L1 regularization tends to concentrate the weight of the network in a relatively small number of high-importance connections, while the other weights are driven toward zero.

Dropout: modify the network itself

We start by randomly (and temporarily) deleting half the hidden neurons in the network, while leaving the input and output neurons untouched. We forward-propagate the input x through the modified network, and then backpropagate the result, also through the modified network. After doing this over a mini-batch of examples, we update the appropriate weights and biases. We then repeat the process, first restoring the dropout neurons, then choosing a new random subset of hidden neurons to delete, estimating the gradient for a different mini-batch, and updating the weights and biases in the network. When we actually run the full network that means that twice as many hidden neurons will be active. To compensate for that, we halve the weights outgoing from the hidden neurons.

It's like averaging many networks. Averaging or voting scheme is often powerful. Because different networks may overfit in different ways, and averaging may help eliminate that kind of overfitting.

 "This technique reduces complex co-adaptations of neurons, since a neuron cannot rely on the presence of particular other neurons. It is, therefore, forced to learn more robust features that are useful in conjunction with many different random subsets of the other neurons."

Dropout is a way of making sure that the model is robust to the loss of any individual piece of evidence. 

Artificially expanding the training data

More training data can sometimes compensate for differences in the machine learning algorithm used.

Weight initialization

Normalized Gaussians to initialization ----problem: saturated neurons on the hidden layer.

Solution: Initialize those weights as Gaussian random variables with mean 0 and standard deviation . Continue to choose the bias as a Gaussian with mean 0 and standard deviation 1, for reasons I'll return to in a moment. 

Exercise:

• Connecting regularization and the improved method of weight initialization L2 regularization sometimes automatically gives us something similar to the new approach to weight initialization. Suppose we are using the old approach to weight initialization. Sketch a heuristic argument that: (1) supposing λ is not too small, the first epochs of training will be dominated almost entirely by weight decay; (2) provided ηλ≪n the weights will decay by a factor of exp(−ηλ/m)ex per epoch; and (3) supposing λλ is not too large, the weight decay will tail off when the weights are down to a size around 1/n−−√1/n, where nn is the total number of weights in the network. Argue that these conditions are all satisfied in the examples graphed in this section.

How to choose a neural networks' hyper-parameters?

1、Some tricks:

Try to train the network to do a easier classification: for example, tell 0 from 1.

Dominite more frequently.

Use a small set of date first. 

Try different learning rate at different epochs.

Use validation accuracy to pick the regularization hyper-parameter, the mini-batch size, and network parameters such as the number of layers and hidden neurons.

2、learning rate: We first use a large learning rate and then switch to a small one.

One natural approach is to use the same basic idea as early stopping. The idea is to hold the learning rate constant until the validation accuracy starts to get worse. Then decrease the learning rate by some amount, say a factor of two or ten. We repeat this many times, until, say, the learning rate is a factor of 1,024 (or 1,000) times lower than the initial value. Then we terminate. For first experiments, the suggestion is to use a single, constant value for the learning rate. 

3、The regularization parameters:

I suggest starting initially with no regularization (λ=0.0), and determining a value for η, as above.

Using that choice of η, we can then use the validation data to select a good value for λ.

Start by trialling λ=1.0, and then increase or decrease by factors of 10, as needed to improve performance on the validation data.

Once you've found a good order of magnitude, you can fine tune your value of λ.

That done, you should return and re-optimize η again.

4、mini-batch size

Using larger mini-batch can speed things up. Because the calculation speed up by the hardware and algebra library.

Too small, and you don't get to take full advantage of the benefits of good matrix libraries optimized for fast hardware. Too large and you're simply not updating your weights often enough: choose a compromise value which maximizes the speed of learning.

5、automated-techniques: grid-search

Other techniques

1、Variations on stochastic gradient descent

Hessian technique:

By Taylor's theorem: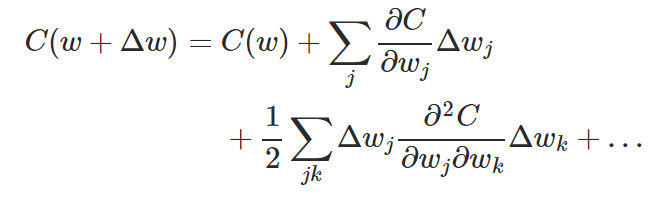 

H: hessian matrix, whose jkth entry is .

The right hand side can be minimized by choosing:  

Algorithm:

 

Advantages: 

1）Hessian methods converge on a minimum in fewer steps than standard gradient descent.

2）In particular, by incorporating information about second-order changes in the cost function it's possible for the Hessian approach to avoid many pathologies that can occur in gradient descent.

3）Furthermore, there are versions of the backpropagation algorithm which can be used to compute the Hessian.

Disadvantage: Hessian H can be too big to store and compute!

Momentum-based gradient descent: with velocity and friction, commonly used and often speed up learning

A new update rule: μ： momentum coefficient, 0<μ<1.

Exercise:

What would go wrong if we used μ>1 in the momentum technique?

What would go wrong if we used μ<0 in the momentum technique?

2、Other models of artificial neurons

tanh: a rescaled version of sigmoid

Advantages: activations can be both positive and negative, which ensures faster descent.

rectified linear neuron: