LU分解法求解线性方程组

LU分解法求解线性方程组

分类： 数值分析 2007-12-03 10:15 13774人阅读 评论(1) 收藏 举报

output 算法 matrix vector string class

算法名称：LU分解法

算法描述：

假定能够把矩阵A写成两个矩阵相乘的形式

                                                     （1）

其中L为下三角矩阵，U为上三角矩阵。

例如，4×4矩阵A的情况，（1）式如下：

 （2）

可以用如（1）式分解来求解线性方程组

                                  （3）

首先求解向量y使得

                                                                               （4）

然后再来求解

                                                      （5）

此拆分方法的优点在于求解一个三角形方程组相当容易，这样，（4）式可用向前替代过程求解，如下：

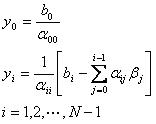                                                （6）

（5）式可用回代过程求解，这与（2）式~（3）式一样，

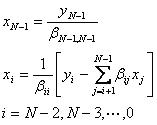                        （7）

（6）式和（7）式共需执行N²次内层循环（对每个右端项b），每个内层循环包括一次乘法和一次加法。如果有N个右端项，它们是单位列向量（在求矩阵逆时就是这种情况），考虑这些零元素可把（6）式的总执行次数从N³/2减少到N³/6，而（7）式的执行次数不变，仍为N³/2。

       注意：一点对A进行了LU分解，就可以一次求解所有要解的右端项。

 

算法实现：

首先，写出（1）式或（2）式的第i，j分量。它总是一个和式，开始部分形式如下：

和式中的项数依赖于i和j中较小的数。事实上有三种形式：

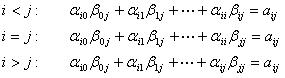                         （8，9，10）

显然，（8）~（10）式共有N²个方程，而要求N²+N个未知的α和β（因对角线的未知元素有两套），既然未知数的个数比方程个数多，就人为指定N各位指数，然后再来求解其他的未知数。事实上，总是令

                                                                          （11）

有一个算法称为Crout算法，它仅按某种次序排列方程，就能容易的求出（8）式~（11）式的N²+N各方程中的所有α和β。步骤如下：

设
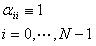    ，即（11）式

对每个j=0,1,2,...,N-1进行以下两步：

第一步，对每个i=0,1,...,j用（8）式、（9）式和（11）式来解β_ij，即

                                                                          （12）

第二步，对每个i=j+1,j+2,...,N-1用（10）式来求解α_ij，即

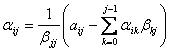                              （13）

在求解下一个j之前要保证进行了以上两步。

 

如果按上述过程进行几次迭代后，就会发现（12）式和（13）式右端的α和β在需要时已经得到，还会发现，每一个a_ij仅被使用一次就不再使用了。这意味着分解是“同址”进行的。简言之Crout算法得到的矩阵是混合矩阵，对本例排列如下：

注：不是把矩阵A分解成LU形式，而是将其按行置换的方式分解。

 

Crout算法的精妙之处：

l         （12）式，在i=j（最后一次应用）时，与（13）式（除后者还要做一次除法外）是完全一样的，这两种情况要求和的上线都是k=j-1（=i-1）。这意味着，不必费心去考虑对角线元素βjj是否会正落在对角线上，也不必考虑该列中，它下面的某个元素（未做除法的）αij，i=j+1，j+2,...,N-1是否会提升成为对角线元素β。

l         它首先找到每行的最大元素，而后（在找最大主元时）乘以一个比例系数，这就实现了“隐式主元法”。

 

运行示例：

Origin coefficient matrix:

 | 0.0 2.0 0.0 1.0 |

 | 2.0 2.0 3.0 2.0 |

 | 4.0 -3.0 0.0 1.0 |

 | 6.0 1.0 -6.0 -5.0 |

-----------------------------------------------

LU mixed matrix:

 | 6.0 1.0 -6.0 -5.0 |

 | 0.0 2.0 0.0 1.0 |

 | 0.3333333333333333 0.8333333333333334 5.0 2.833333333333333 |

 | 0.6666666666666666 -1.8333333333333333 0.8 3.8999999999999995 |

-----------------------------------------------

Origin left-hand vector b:

 | 0.0 |

 | -2.0 |

 | -7.0 |

 | 6.0 |

-----------------------------------------------

Final solution vector:

 | -0.5000000000000003 |

 | 1.0000000000000002 |

 | 0.33333333333333337 |

 | -2.0000000000000004 |

-----------------------------------------------

 

示例程序： 

package  com.nc4nr.chapter02.lu;

public   class  LU  {

    // 4 * 4 coefficient matrix a
    double[][] a = {
            {0.0, 2.0, 0.0, 1.0},
            {2.0, 2.0, 3.0, 2.0},
            {4.0, -3.0, 0.0, 1.0},
            {6.0, 1.0, -6.0, -5.0}
    };
    
    // 4 * 1 coefficient matrix b
    double[] b = {
            0.0,
            -2.0,
            -7.0,
            6.0
    };
    
    int anrow = 4;
    int[] indx = new int[anrow];
    int parity = 1;
    
    private void lucmp() {
        final double tiny = 1.0e-20;
        int imax = 0, n = anrow;
        double big, dum, sum, temp;
        double[] vv = new double[n];
        
        System.out.println("Origin coefficient matrix:");
        output(a,4);
        
        for (int i = 0; i < n; i++) {
            big = 0.0;
            for (int j = 0; j < n; j++) {
                if ((temp = Math.abs(a[i][j])) > big) big = temp;
            }
            if (big == 0.0) System.out.println("lu: singular matrix in lucmp.");
            vv[i] = 1.0/big;
        }
        
        for (int j = 0; j < n; j++) {
            for (int i = 0; i < j; i++) {
                sum = a[i][j];
                for (int k = 0; k < i; k++) sum -= a[i][k]*a[k][j];
                a[i][j] = sum;
            }
            big = 0.0;
            for (int i = j; i < n; i++) {
                sum = a[i][j];
                for (int k = 0; k < j; k++)    sum -= a[i][k]*a[k][j];
                a[i][j] = sum;
                if ((dum = vv[i]*Math.abs(sum)) >= big) {
                    big = dum;
                    imax = i;
                }
            }
            if (j != imax) {
                for(int k = 0; k < n; k++) {
                    dum = a[imax][k];
                    a[imax][k] = a[j][k];
                    a[j][k] = dum;
                }
                parity = -parity;
                dum = vv[imax];
                vv[imax] = vv[j];
                vv[j] = dum;
            }
            indx[j] = imax;
            if (a[j][j] == 0.0) a[j][j] = tiny;
            if (j != n - 1) {
                dum = 1.0/a[j][j];
                for (int i = j+1; i < n; i++) a[i][j] *= dum;
            }
        }
        
        System.out.println("LU mixed matrix:");
        output(a,4);
    }
    
    private void lubksb() {
        double sum;
        int n = anrow, ii = 0;
        
        System.out.println("Origin left-hand vector b:");
        output(b,4);
        
        for (int i = 0; i < n; i++) {
            int ip = indx[i];
            sum = b[ip];
            b[ip] = b[i];
            if (ii != 0)
                for (int j = ii - 1; j < i; j++) sum -= a[i][j]*b[j];
            else if (sum != 0.0) 
                ii = i + 1;
            b[i] = sum;
        }
        for (int i = n-1; i >= 0; i--) {
            sum = b[i];
            for(int j = i + 1; j < n; j++) sum -= a[i][j]*b[j];
            b[i] = sum / a[i][i];
        }
        System.out.println("Final solution vector:");
        output(b,4);
    }
    
    private void output(double a[][], int anrow) {
        for (int i = 0; i < anrow; i++) {
            System.out.println(" | " + a[i][0] + " " + 
                    a[i][1] + " " + 
                    a[i][2] + " " + 
                    a[i][3] + " | ");
        }
        System.out.println("-----------------------------------------------");
    }
    
    private void output(double[] b, int bnrow) {
        for (int i = 0; i < bnrow; i++) {
            System.out.println(" | " + b[i] + " | ");
        }
        System.out.println("-----------------------------------------------");
    }
    
    public LU() {
        lucmp(); // 分解
        lubksb(); // 回代
    }
    
    public static void main(String[] args) {
        new LU();
    }

}