《目录》
矩阵基础
在游戏开发中,游戏对象的 平移、旋转 和 缩放 都会涉及到矩阵的使用。而在OpenGL中,基本使用的转换方法也都是矩阵,所以,矩阵在游戏开发中是必须要掌握的数学知识。要了解游戏中对象的 平移 、旋转 和 缩放
1. 矩阵的定义:
m x n 阶矩阵
由 m × n 个数 aij 排成的m行n列的数表称为m行n列的矩阵,简称m × n矩阵。记作:
这 m×n 个数称为矩阵A的元素,简称为元,数 aij 位于矩阵 A 的第 i 行第 j 列,称为矩阵 A 的 (i,j) 元,以数 aij 为 (i,j) 元的矩阵可记为 (aij) 或 (aij)m × n,m×n 矩阵 A 也记作 Amn。
n 阶矩阵
行数 与 列数 都等于 n 的矩阵称为 n阶矩阵 或 n阶方阵。
单位矩阵
n阶方阵,且对角元素为1,其他元素为0的矩阵。
实矩阵与复矩阵
元素是 实数 的矩阵称为 实矩阵,元素是 复数 的矩阵称为 复矩阵。
2. 矩阵的基本运算:
矩阵的基本运算包括矩阵的 加法,减法,数乘,转置,共轭 ,共轭转置 和 矩阵的逆 ,以及最重要的 乘法 。在游戏中的转换运用,用的基本都是乘法的性质。
《加法、 减法、 数乘》
矩阵的加减法和矩阵的数乘合称矩阵的线性运算。
1. 加法:
矩阵的加法满足下列运算律(A,B,C必须都是 同型矩阵 ):
具体如下:
2. 减法
同矩阵的假发一样,满足以下运算规律(A,B,C必须都是 同型矩阵 ):
具体如下:
3.数乘(与实数相乘)
矩阵的数乘满足以下规律:
《转置、 共轭、 共轭转置、 矩阵的逆》
1. 转置
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵,这一过程称为矩阵的转置;
矩阵的转置满足以下运算律:
2. 共轭
矩阵的共轭定义为:
例如:一个2X2的复数矩阵,其共轭方式如下
3. 共轭转置
矩阵的共轭转置定义为:
也可以写成:
例如:一个2X2的复数矩,其共轭转置方式如下
4. 矩阵的逆
矩阵的共轭转置定义为:
对于一个 n阶矩阵 A,若存在一个 n阶矩阵 B,使得 AB=BA=In,则称 B 是 A 的 逆矩阵,记为 B=A-1;
《矩阵的行列式》
一个n×n的正方矩阵A的行列式记为 det(A) 或者 |A| ;
一个3×3矩阵的行列式可表示如下:
《乘法》
两个矩阵的乘法仅当第一个矩阵 Amp 的列数 p 和另一个矩阵 Bpn 的行数 p 相等时,才能定义。
其满足 结合律 和 分配律;
例如:一个2×3矩阵与3×2矩阵相乘,如下
游戏中的矩阵应用(2D)
1. 基础二维变换:
《二维的向量操作》
1. 平移变换 (translation transformation)
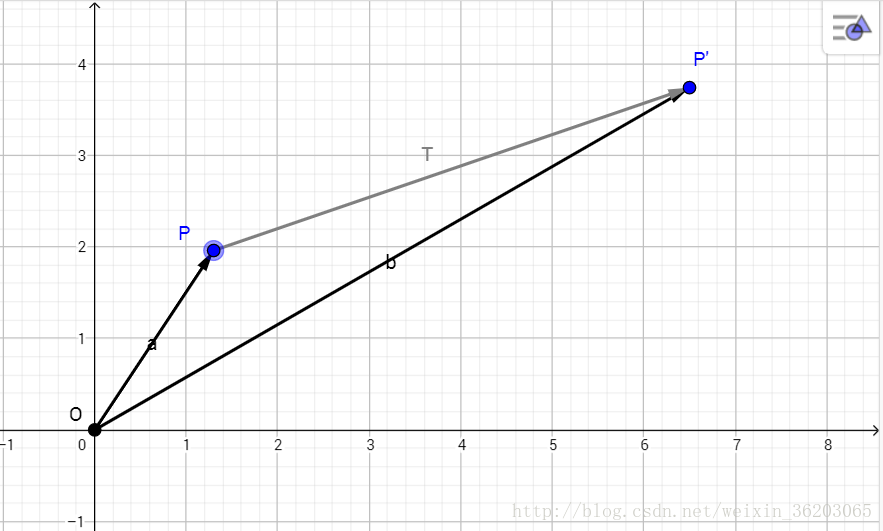
将点 P(x, y)在 x轴方向、 y轴方向分别平移距离 tx, ty,得到点 P´(x׳, y׳),则:
图示:
矩阵表示:
2. 旋转变换(rotation transformation)
点 P(x, y)的极坐标表示(r为P 到原点的距离)
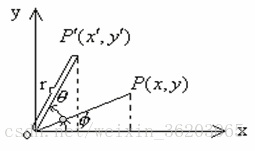
绕坐标原点(称为参照点,基准点)旋转角度θ (逆时针为正,顺时针为负)
即:
矩阵表示:
3. 缩放变换(scaling transformation)
将点P(x, y)在x方向, y方向分别放缩 sx 和 sy 倍,得到点P´(x׳, y׳)
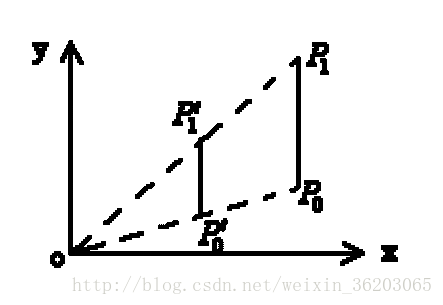
以坐标原点为放缩参照(基准)点不仅改变了物体的大小和形状,也改变了它离原点的距离
即:
矩阵表示:
《平移、旋转、缩放操作的统一运算:矩阵》
1. 齐次坐标(Homogeneous Coordinate)
为什么需要齐次坐标?
齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。例如,二维点(x,y)的齐次坐标表示为(hx,hy,h)。
由此可以看出,一个向量的齐次表示并不是唯一的,齐次坐标的h取不同的值都表示的是同一个点,比如齐次坐标(8,4,2)、(4,2,1)表示的都是二维点(4,2);
直接使用上方各个形式不统一的矩阵,会带来很多的不便:
①由于形式不统一,进行多种变换时,计算量会很大;
②同时,运算的形式也不统一,平移为“+”,旋转缩放为“×”;
定义
(x,y)点对应的齐次坐标定义为(xh,yh,h);
标准齐次坐标 (x,y,1), h=0表示无穷远点
2. 二维变换的统一矩阵表示
统一表示的优点:
①便于变换合成连续变换时,可以先得到变换的矩阵;
②便于硬件实现;
①平移矩阵 T(tx,ty)
②旋转矩阵 R(θ)
③缩放矩阵 S(sx,sy)
3. 变换的性质
①平移和旋转变换具有可加性
②放缩变换具有可乘性
4. 逆变换
①逆平移变换
②逆旋转变换
③逆缩放变换
2. 复合变换(Composite transformation):
变换合成时,矩阵相乘的顺序:先作用的放在连乘的右端,后作用的放在连乘的左端;
《变换合成》
连续变换时,先计算变换矩阵,再计算坐标;
优点1:提高了对图形依次做多次变换的运算效率
如:图形上有n个顶点Pi,如果依次施加的变换为T,R(即先平移后旋转),那么顶点Pi 变换后的坐标为:
优点2:能构造复杂的变换矩阵
对图形作较复杂的变换时,不直接去计算这个变换,而是将其先分解成多个基本变换,再合成总的变换。
多个变换的组合,可通过单个变换矩阵来计算矩阵乘积;
《连续变换》
1. 连续平移
平移向量为(t1x,t1y)和(t2x,t2y),点P 经变换为P´,则有:
2. 连续旋转
P 经连续旋转角度分别为θ 1和θ 2后:
3. 连续缩放
连续放缩因子分别为:(s1x, s1y) 和 (s2x, s2y)
3. 基于任意参照点的二维变换:
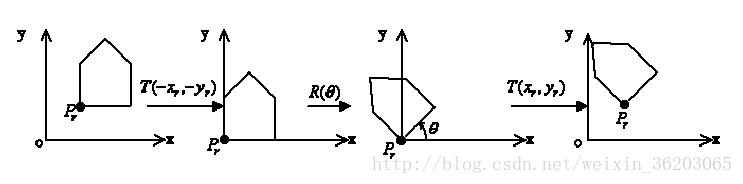
《任意点的旋转变换》
步骤:
①平移对象使参照(基准)点移到原点
②绕坐标原点旋转
③平移对象使基准点回到原始位置
《任意点的缩放变换》
步骤:
①平移对象使基准点与坐标原点重合
②放缩变换
③反向平移使得基准点回到初始位置
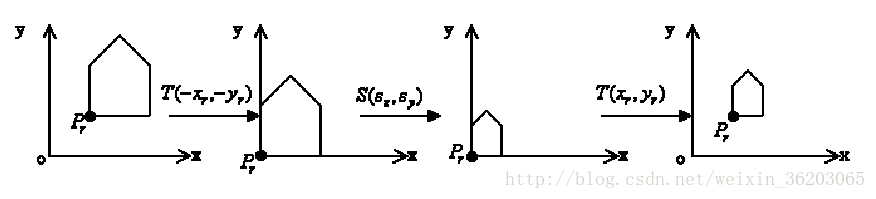
游戏中的矩阵应用(3D)
等待补充…





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








