有理函数内插法和外推法算法实现

算法名称：有理函数内插法和外推法

 

算法描述：

用R_{i(i+1)...(i+m)}表示过m+1个点(x_i,y_i)...(x_i+m,y_i+m)的有理函数。假定

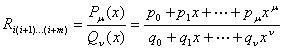                  （1）

因为有μ+ν+1个未知的p和q（q₀任意），则有

                                （2）

在把插值函数定义为有理函数时，必须给出分子和分母多项式的阶数。

      有理函数比多项式函数优越，是因为有理函数能够模拟具有极点的函数。极点是指（1）式中分母的零点。如果要插值的函数本身有极点的话，则在实数x处就有可能出现这些极点。

      若函数f（x）对所有有限实数x都是有穷的，但在x复平面内存在极点的解析连续性。即使限定为实数x，这些极点也会使多项式逼近彻底失败，正如它们会使x的无穷级数达不到收敛一样。如果在复平面内，沿列表中的m个点画一个圆，除非最近的极点也远离此圆，否则多项式插值结果就不会很好。相比而言，只要在有理函数的分母中，x有足够高的幂次以避免（消除）近处的极点，有理函数的逼近效果要强于多项式函数逼近。

      Bulirsch-Stoer算法产生一个所谓的对角有理函数，分子和分母阶数相等（若m为偶数），或者分母的阶数比分子的阶数高一阶（若m为奇数）。

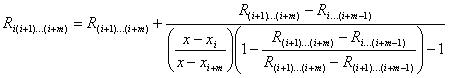        （3）

该递推式表示，可由过m个点的有理函数和过m-1个点的有理函数导出过m+1个点的有理函数。初始值为

                                      （4）

及

                 （5）

于是跟《多项式内插法和外推法》一文中的（4）式和（5）式一个道理，可以将（3）转化为仅含细微差别的式子

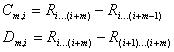                        （6）

特别注意它们满足关系式，这对后面的式子理解非常重要

                        （7）

由上式可得

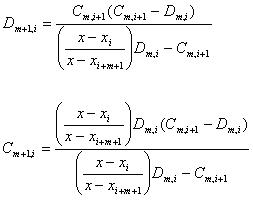                 （8）

      这个方法的式子很复杂，笔者感觉（3）式看得实在恶心，但是理解了基本思想还是不成问题的，这里我们讨论的有理函数插值法和多项式函数插值法都是由拉格朗日插值多项式衍生而来的，结合拉格朗日插值多项式的思想会更容易理解一些。

     

注：在程序实现时我们其实只需用到（8）式，所以前面的只是了解就可以了。

 

运行示例：