二、非均匀B样条或非均匀有理B样条（NURBS）

Tangsong_xu

已于 2023-11-16 09:45:25 修改

阅读量7.6k

点赞数 14

分类专栏：路径规划几何文章标签：算法

于 2023-11-15 20:52:33 首次发布

本文链接：https://blog.csdn.net/Tangsong_xu/article/details/134426243

版权

0、

本博客是我在学习的时候翻译前人博客的版本，大家多多反馈。
感谢“密歇根理工大学--计算机科学系--Dr. C.-K. Shene 教授”做出的杰出贡献。

1、动机

B 样条曲线是多项式曲线。虽然它们很灵活，而且有许多很好的曲线设计属性，然而它们无法表示最简单的曲线：圆。正如有理曲线页面上所讨论的，圆只能用有理函数（即两个多项式的商）。应对圆形、椭圆和许多其他不能用多项式表示的曲线，我们需要扩展到 B 样条曲线。

圆是2次曲线。让我们来看看b样条是为何不能表示它的。下面是四条有8个控制点的闭合b样条曲线。从左到右的节点重复度分别是2、3、5和10。2节点重复度形成的闭b样条曲线看起来不像一个圆。相反，它看起来像一个圆形的正方形。3节点重复度曲线看起来更好一些。度越大，曲线的“圆度”越好。10节点重复度闭合曲线与圆非常相似;但是，它不是一个圆。即使你可以接受这个b样条曲线的10度作为一个圆，那就过分了!为什么2次曲线要用10节点重复度b样条曲线来表示?

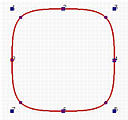
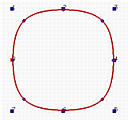
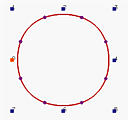
为了解决这个问题，我们将使用齐次坐标将 B 样条推广到有理曲线。因此，我们得名 Non-Uniform Rational B-Splines（NURBS）。

2、定义

让我们考虑如何将齐次坐标引入b样条曲线，并推导出NURBS定义。

给定n+1个控制点P0, P1，…， Pn和结向量U = {u0, u1，…， um}为m+1节时，由这些参数定义的p次b样条曲线如下:

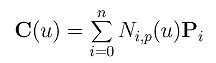
设控制点Pi改写为具有四个分量的列向量，其中第四个分量为1:

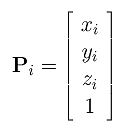
我们可以把这个看做齐次坐标。由于将一个点(齐次形式)的坐标与一个非零数相乘不会改变点的位置，我们将Pi的坐标与权重wi相乘，得到齐次坐标的新形式:

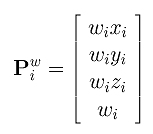
注意Pwi和Pi表示齐次坐标中的同一点。将新的齐次形式代入上述b样条曲线方程，可得:

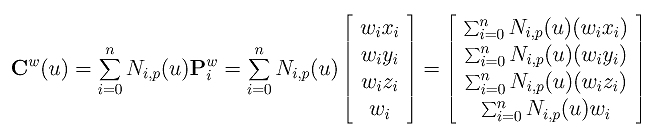
因此，点Cw(u)为齐次坐标形式的原始b样条曲线。现在，让我们用第四个坐标除以Cw(u)，将其转换回笛卡尔坐标:

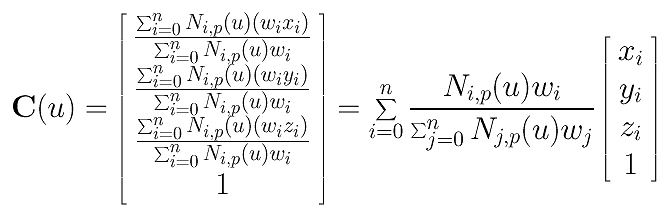
最后，我们用简洁的形式表示如下:

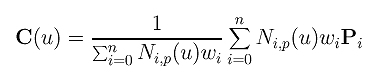
这是由控制点P0, P1，…定义的p次NURBS曲线， Pn，结向量U = {u0, u1，…， um}，权重为w0, w1， .., wn。注意，由于权重wi与控制点Pi作为其第四个分量相关联，权重的数量必须与控制点的数量一致。

总体而言，权重wi为正;但负权重有着有趣的现象：如果一个权重，例如wi，变为零，Pi的系数为零，因此，控制点Pi对任何u的C(u)计算都没有影响(即Pi是“禁用的”)。此外，零权重还有一个非常有用的解释，称为无限控制点

两个直接结果

以下是根据上述定义可以立即得到的两个结果。

如果所有权值都等于1，则NURBS曲线简化为b样条曲线。
这是很明显的，因为在这种情况下，齐次形式的控制点和传统的笛卡尔形式是一样的，分母是1。
NURBS曲线是有理的
这也是显而易见的。与控制点Pi, Ni,p(u)wi相乘的值是p次多项式，分母是所有系数的和，因此也是p次多项式，因此控制点Pi的系数是p次多项式的商，函数C(u)是有理函数。

这两个结果表明b样条曲线是NURBS曲线的特殊情况。此外，由于NURBS曲线是有理的，圆，椭圆和许多其他曲线是不可能用b样条曲线表示的，但是现在可以用NURBS曲线表示了。

几何解释

NURBS曲线是一种特殊的曲线吗?事实证明，它们并不是。事实上，它们只是b样条曲线的另一个形式（推广）。考虑控制点Pwi = (wixi, wiyi, wizi, wi)。这个点有四个分量，可以看作是四维空间中的一个点，因此，下面的C(u)就变成了四维空间中的b样条曲线:

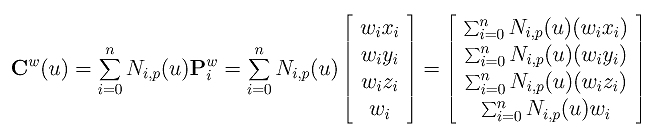
在讨论齐次坐标的几何解释时，将前三个坐标分量除以第四个分量相当于将一个四维点投影到平面w = 1。由于上述曲线是通过前三个坐标除以第四个坐标转换为NURBS曲线的，因此我们可以得出，三维空间中的NURBS曲线只是b样条曲线在四维空间中的投影。因此，如果我们很好地理解了b样条曲线，我们应该能够很容易地理解NURBS曲线。

3、重要性质

给定一组n+1个控制点P0, P1，…， Pn，每一个都与一个非负权值wi相关联(即Pi具有权值wi >= 0)，以及一个结向量U = {u0, u1，…， um}为m+1节时，p次NURBS曲线定义如下:

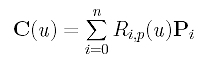
其中 RI，P（U）定义如下：

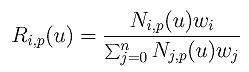
之所以使用不同的表示法，是因为我们想以尽可能按照b样条曲线的形式重写NURBS曲线的定义。在上述表示法中，Ri,p(u)是NURBS基函数。

NURBS 基函数的重要性质

由于NURBS是b样条的推广，它应该具有b样条的所有性质。下面是一些最重要的NURBS基函数。请将它们与b样条基函数进行比较。

Ri,p(u)是u上的p次有理函数。
非负性——对于所有i和p, Ri,p(u)是非负的。
本地支持——Ri,p(u)在[ui,ui+p+1]上是非零的。
由于Ni,p(u)在[ui,ui+p+1)上是非零的，Ri,p(u)也是。注意，我们假设wi是非负的。
在任何结点跨度[ui, ui+1)上，最多p+1次p基函数是非零的，即:Ri-p,p(u)， Ri-p+1,p(u)， Ri-p+2,p(u)，…， Ri,p(u)。
单位划分——所有非零次p基函数在span [ui, ui+1)上的和为1。
若结点个数为m+1，基函数的次数为p，且p个基函数的次数为n+1，则m = n+ p +1:
基函数Ri,p(u)是一条p次有理函数的复合曲线，连接点在[ui, ui+p+1)的结点处。
在重复度为k的结上，基函数Ri,p(u)是Cp-k连续的。
因此，增加多样性会降低连续性，增加重复度会增加连续性。
如果对于所有i，满足wi = c，其中c是一个非零常数，则Ri,p(u) = Ni,p(u)
因此，b样条基函数是NURBS基函数在所有权值都成为非零常数时的特殊情况。我们已经提到了c = 1的特殊情况。