HDU2481 Toy【Burnside + 生成函数求递推式】

题目描述：

一个n+1个点，2n条边的图如下：

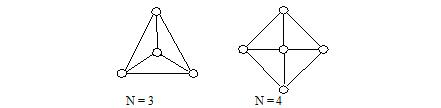
现在要删除n条边使其成为一棵树，问有多少种不同的方案数，旋转算相同。
答案mod m，n,m<=10⁹

题目分析：

首先Burnside一波转化为求一个置换下的不动点数，再枚举gcd变成求长度为$k$的环加上中间的点的生成树个数。

分为两种情况：

• 如果1和$k^{\prime }$没有连通，设$f[i]$表示前$i$个点构成生成树的方案数。枚举在哪个点断开进行转移，得到$f[i]={\sum }_{j=0}^{i-1}f[j]\ast (i-j)$
  但是显然这个式子没法矩阵加速，但是它的形式又这么优美，我们尝试把它写成一个封闭形式，记$f$的生成函数为$F(x)={\sum }_{i=0}^{\infty }{f}_i\ast x^i$.
  递推式是一个卷积形式，设$G(x)={\sum }_{i=0}^{\infty }i\ast x^i$，得到：
  $$F(x)=F(x)\ast G(x)+1$$
  （$+1$是因为$f[0]=1$）
  移项得：$$F(x)=\frac{1}{1-G(x)}$$
  而$G(x)={\sum }_{i=0}^{\infty }i\ast x^i=x\ast {\sum }_{i=1}^{\infty }i\ast x^{i-1}=x\ast (\frac{1}{1-x}{)}^{\prime }=\frac{x}{(1-x{)}^2}$
  带入化简得到$F(x)=\frac{x^2-2x+1}{x^2-3x+1}$，移项得
  $$F(x)-3xF(x)+x^{2}F(x)=x^2-2x+1$$
  由左右两边$x^i$对应系数相等，得到：
  $$\begin{array}{rl}{f}_n-3\ast f_{n-1}+f_{n-2}& =0(n\ge 3)\\ f_2-3\ast f_1+f_0& =1\\ f_1-3\ast f_0& =-2\\ f_0& =1\end{array}$$
  可得$f_0=1,f_1=1,f_2=3,f_3=3f_2-f_1=8\dots$
  然后矩阵加速即可。

• 如果1和$k^{\prime }$连通，那么还要在$1$到$k$之间找两条边（可以相同）断开，枚举1所在的连通块的长度$i$，中间还剩$k-i$个点方案为$f[k-i]$。所以$g_k={\sum }_{i=2}^{k}i\ast (i-1)\ast f[k-i]$，设g的生成函数为$P(x)$

  同理可以配一个$H(x)={\sum }_{i=2}^{\infty }i\ast (i-1)x^i=(\frac{1}{1-x}{)}^{\prime \prime }{x}^2$
  那么$$P(x)=H(x)\ast F(x)=\frac{2x^2}{(1-x{)}^3}\ast \frac{x^2-2x+1}{x^2-3x+1}=\frac{2x^2}{(1-x)(x^2-3x+1)}$$
  移项得$$(1-4x+4x^2-x^3)P(x)=2x^2$$
  同样，对比系数得到：
  $$\begin{array}{rl}{g}_n-4\ast g_{n-1}+4\ast g_{n-2}-g_{n-3}& =0(n\ge 3)\\ g_2-g_1+4\ast g_0& =2\\ g_1-4\ast g_0& =0\\ g_0& =0\end{array}$$
  可得$g_0=0,g_1=0,g_2=2,g_3=4g_2-4g_1+g_0=8\dots$
  矩阵加速即可。

最后的答案就是$f_k+g_k$。由于Burnside最后要除$n$，可能没有逆元，可以用$a/b\%c=a\%(bc)/b$，令$\mathrm{m}\mathrm{o}\mathrm{d}=n\ast m$，中间的乘法要用大整数快速乘。

另外，此题也有其他求解递推式的方法，例如利用前缀和以及错位相消，以及利用矩阵数定理直接求行列式，再求行列式的递推式

Code：

#include<bits/stdc++.h>
#define LL long long
using namespace std;
int n,m,p[3005],d[3005],cnt;
LL mod,ans;
inline LL mul(LL a,LL b){LL r=a*b-(LL)((long double)a/mod*b+0.5)*mod;return r<0?r+mod:r;}
struct Mat{
    LL s[3][3];int o;
    Mat(){memset(s,0,sizeof s);}
    void reset(int x){
        if(!x) s[0][0]=3,s[0][1]=1,s[1][0]=s[1][1]=0,o=2;
        else if(x==1) s[0][0]=3,s[1][0]=-1,s[0][1]=1,s[1][1]=0,o=2;
        else if(x==2) memset(s,0,sizeof s),s[0][0]=2,o=3;
        else memset(s,0,sizeof s),s[0][0]=4,s[1][0]=-4,s[2][0]=1,s[0][1]=s[1][2]=1,o=3;
    }
    Mat operator * (const Mat &B)const{
        Mat ret;ret.o=o;
        for(int k=0;k<o;k++) for(int i=0;i<o;i++) for(int j=0;j<o;j++)
            ret.s[i][j]=(ret.s[i][j]+mul(s[i][k],B.s[k][j]))%mod;
        return ret;
    }
}f,g;
LL calc(int N){
    if(N<=1) return 1;
    int tmp=N;
    for(N-=2,f.reset(0),g.reset(1);N;N>>=1,g=g*g) if(N&1) f=f*g;
    LL ret=f.s[0][0]; N=tmp;
    for(N-=2,f.reset(2),g.reset(3);N;N>>=1,g=g*g) if(N&1) f=f*g;
    return (ret+f.s[0][0]+2*mod)%mod;
}
void dfs(int i,int x,int phi){
    if(i>cnt) {ans=(ans+mul(phi,calc(n/x)))%mod;return;}
    for(int j=0;j<=d[i];j++) dfs(i+1,x,phi),x*=p[i],phi*=p[i]-bool(!j);
}
int main()
{
    while(~scanf("%d%d",&n,&m)){
        mod=1ll*n*m,ans=cnt=0; int x=n;
        for(int i=2;i*i<=x;i++) if(x%i==0) {p[++cnt]=i,d[cnt]=0;while(x%i==0) x/=i,d[cnt]++;}
        if(x>1) p[++cnt]=x,d[cnt]=1;
        dfs(1,1,1);
        printf("%lld\n",ans/n);
    }
}

$Upd:$ 求$g_k$其实可以看做在中间断一条边，然后可以左边向环中央那个点连边，右边不动，方案为${\sum }_{i=1}^{k-1}f[i]$，右边连边同理。所以最后的答案就是$2\ast {\sum }_{i=1}^{k-1}f[i]+f[k]$，对$f$矩阵加速的时候带上一个前缀和即可。