EBlearn中画sigmoid函数的多项式拟合方法

上机器视觉和模式识别讨论课，我讲EBM（energy-based models），接触到EBLearn，Eblearn是一个开源的深度学习软件包，用C++语言写的。在源代码eblearn_1.2_r2631\core\libidx\src\numerics.cpp文件中发现了用三阶多项式插值拟合的方法，觉得这种计算方法很有工程性味道，且针对特定问题很有用。

代码如下：

// standard sigmoid 

// Rational polynomial for computing 1.71593428 tanh (0.66666666 x)

#define PR  ((float)0.66666666)
#define PO  ((float)1.71593428)
#define A0   ((float)(1.0))
#define A1   ((float)(0.125*PR))
#define A2   ((float)(0.0078125*PR*PR))
#define A3   ((float)(0.000325520833333*PR*PR*PR))
#define Fone	((float)1.0)
#define Fzero 	((float)0.0)

float stdsigmoid(float x) {
	register float y;

	if (x >= Fzero)
		if (x < (float)13)
			y = A0+x*(A1+x*(A2+x*(A3)));
		else
			return PO;
	else
		if (x > -(float)13)
			y = A0-x*(A1-x*(A2-x*(A3)));
		else
			return -PO;

	y *= y;
	y *= y;
	y *= y;
	y *= y;
	return (x > Fzero) ? PO*(y-Fone)/(y+Fone) : PO*(Fone-y)/(y+Fone);
}

先将程序输出到两个数组，然后在matlab下显示得到下面结果：

sigmoid函数的相关知识

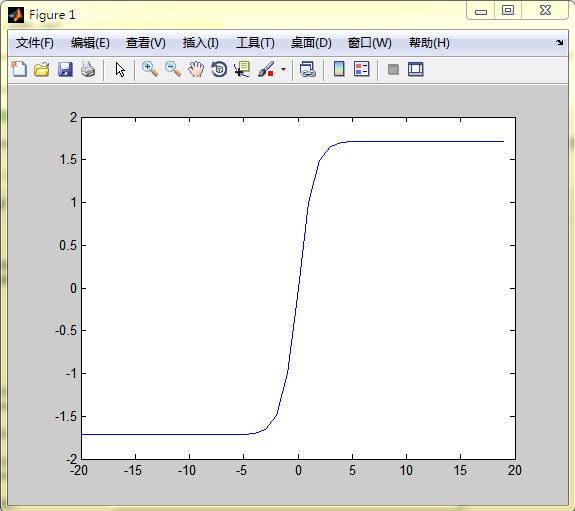
1.奇函数，且在区间[-1,1]之间是条直线，即近似线性的，从上图中可以看出。

2.反函数是,这个函数可以作为指数分布族 中的参数，在吴恩达的机器学习公开课上有关于sigmoid从伯努利分布中推导出来的过程。

3.bipolar logistic function 

（**转载请注明作者和出处**：http://blog.csdn.net/CHIERYU**未经允许请勿用于商业用途**）