1. 卡方分布。
1.1 什么是卡方分布?
在1900年初,英国统计学家卡尔·皮尔逊为了衡量观察频数与理论频数之间的偏差,提出了卡方检验,从而引入了卡方分布的概念。卡方分布是一种特殊的概率分布,它是多个独立的标准正态分布的平方和的分布。
为了直观理解卡方分布,让我们通过一个简单的例子来说明。假设我们有一枚完美的六面骰子,我们希望验证这个骰子是否公平。我们把它投掷600次,按理论,每一面出现的次数应该是100次。但实际上,每一面出现的次数总会有所不同。通过计算每一面出现次数与理论值之间的偏差,我们可以利用卡方分布来判断这个骰子是否真的公平。
如何使用卡方检验验证骰子是否公平:
1. 设定零假设和备择假设:
- 零假设(H0):骰子是公平的,即每一面出现的概率相等。
- 备择假设(H1):骰子不公平,至少有一面出现的概率与其他面不同。
2. 收集数据:假设我们投掷骰子600次,记录下每一面出现的次数。
3. 计算预期频数:如果骰子是公平的,那么我们预期每一面出现的次数为 600 /6 = 100次。
4. 计算卡方统计量:公式为
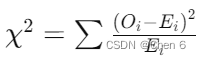 ,
,
其中 Oi 是观测频数,Ei是预期频数。对于骰子的每一面,我们都计算 (Oi - Ei)^2 / Ei,然后将这六个值相加,得到卡方统计量。
5. 确定显著性水平:通常情况下,我们可能会选择0.05作为显著性水平。
6. 查找卡方分布表:根据自由度(在这个例子中是6-1=5)和显著性水平(比如0.05),我们可以在卡方分布表中找到临界值。
7. 作出结论:如果计算出的卡方统计量大于卡方分布表中的临界值,我们拒绝零假设,认为骰子不公平;如果小于或等于临界值,我们没有足够的证据拒绝零假设,因此不能认为骰子不公平。
(注意:在卡方检验中,自由度的概念与我们设置约束条件的数量有关。对于骰子的例子,虽然骰子有6个面,但自由度是5,这是因为总频数(在这个案例中是投掷次数,比如600次)是一个固定的约束条件。
让我们更深入地解释一下:
- 当我们说每一面出现的次数期望为100(假设投掷600次,每一面出现的概率都是1/6),这个期望值是基于总投掷次数600这个固定的总和。
- 当你知道了前5个面出现的次数之后(假设是面1到面5),那么第6个面出现的次数实际上已经被确定了,因为所有面出现的次数之和必须等于600。换句话说,最后一个面出现的次数并不是自由的;它是由前5个面出现次数的结果所决定的。
因此,尽管骰子有6个面,但实际上只有5个自由度,因为总次数的约束导致了最后一个频数值是由前面的频数值确定的。在统计学中,自由度通常定义为独立观测的数量减去被施加的独立约束的数量。在卡方检验的上下文中,这意味着我们有6个独立的观测(每个面的出现次数)和1个约束条件(总次数),因此自由度为 \(6 - 1 = 5\)。)
1.2 卡方分布的性质:
卡方分布的数学性质是统计学中的重要内容,以下是一些核心的性质及其简要的证明概述:
1. 定义和性质
定义:如果k个独立的随机变量Z1, Z2,..., Zk都服从标准正态分布N(0,1),那么这些随机变量平方和的分布称为自由度为k的卡方分布。其数学表示为:
性质:
非负性:卡方分布是非负的,即Q >0。
均值和方差:如果Q服从自由度为\(k\)的卡方分布,那么其均值E[Q] = k,方差Var[Q] = 2k。
可加性:如果Q1和Q2是两个独立的卡方分布变量,分别具有自由度k1和k2,那么它们的和Q1 + Q2也服从卡方分布,自由度为k1 + k2。
2. 证明概述

2. F分布
2.1 什么是F分布
F分布,有时也被称为方差比分布,是一种非常有趣且具有广泛应用的概率分布。
想象一下,我们有两组数据,每组数据都来自于不同的正态分布总体。我们对这两组数据各自进行方差分析,得到了两个方差值。现在,我们想要比较这两个方差,看看它们是否显著不同。这正是F分布闪亮登场的时刻。
F分布是由两个独立的卡方分布的比值形成的。如果我们将两个卡方分布变量,每个变量都除以其对应的自由度,然后再将其中一个除以另一个,我们得到的这个比值就遵循F分布。这个过程可以用一个非常简洁的公式来描述:
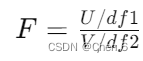 ,
,
其中U和V是两个独立的卡方分布变量,df1和df2分别是它们的自由度。
F分布的美妙之处在于它的形状和参数。F分布的形状由两个自由度参数决定,这意味着我们可以通过调整这两个参数来改变分布的形状。这种灵活性使F分布成为比较两个方差的理想工具。
在实际应用中,F分布通常用于方差分析(ANOVA)和回归分析。它允许我们检验不同组别之间是否存在显著的方差差异,从而帮助我们理解数据中的潜在模式和结构。
当然,我将通过一个方差分析(ANOVA)的例子,来展示F分布在实际中的用处。
假设我们是一个大学的教育研究小组,正在研究三种不同的教学方法对学生考试成绩的影响。我们的目标是判断这三种方法是否存在显著差异,即它们是否对学生的考试成绩有不同的影响。这三种教学方法分别为:传统讲授法(A),协作学习法(B),以及基于项目的学习法(C)。我们随机选取了一批学生,将他们分为三组,每组使用一种教学方法,然后比较这三组学生的考试成绩。
在进行方差分析时,我们首先计算组内方差,即同一组内不同学生考试成绩的方差。这反映了在同一教学方法下学生成绩的波动程度。接下来,我们计算组间方差,即不同组(即不同教学方法)学生平均成绩之间的方差。这反映了不同教学方法对学生成绩的影响程度。
接下来的关键步骤是使用F检验来判断这些方差是否显著。具体来说,我们计算F统计量,这是组间方差与组内方差的比值。根据F分布,我们可以确定在零假设(即所有教学方法的效果相同)为真的情况下,获得当前或更极端F统计量值的概率(即P值)。
如果P值小于我们设定的显著性水平(例如0.05),我们就有足够的证据拒绝零假设,接受备择假设——即至少有一种教学方法的效果与其他方法显著不同。这意味着,我们的实验结果显示,不同的教学方法对学生的考试成绩有显著影响。
通过这个例子,我们可以看到F分布在比较不同组间方差时的用处。它不仅帮助我们确定不同教学方法的效果是否有显著差异,而且还为我们进一步探索哪些具体方法更有效提供了基础。这种分析方法在教育研究、心理学、生物学等众多领域都有广泛的应用。

3. t分布
t分布,也称为学生t分布,是统计学中一个非常重要的概率分布。它由威廉·戈塞特在1908年发表,由于当时的出版政策,他使用了“Student”这个笔名,因此这个分布也被称为学生分布。t分布在样本量较小且总体标准差未知时,特别是在进行假设检验和构建置信区间时,非常有用。
t分布的定义和性质
t分布是一种对称分布,围绕零(均值为零)对称,并且其形状由自由度(df)控制。自由度通常与样本量有关,具体来说,对于从总体中抽取的样本,自由度等于样本量减一(df = n - 1)。
主要性质包括:
1. 对称性:t分布是关于其均值对称的,均值为零。
2. 单峰性:t分布是单峰的,即它有一个明显的最高点,在零点处。
3. 尾部厚度:与正态分布相比,t分布的尾部更厚、更重。这意味着相对于正态分布,t分布在尾部有更多的概率质量,从而在尾部产生极值的可能性更高。
4. 随自由度的变化:随着自由度的增加,t分布逐渐接近正态分布。当自由度趋向于无穷大时,t分布就变成了标准正态分布。
5. 均值和方差:t分布的均值为0(对于自由度大于1的情况),方差为df / df - 2(对于自由度大于2的情况)。这表明,当自由度较低时,t分布的方差大于1,反映了在样本量较小时估计的不确定性更大。
应用
t分布在统计学中的应用非常广泛,特别是在以下方面:
1. 置信区间的计算:在总体标准差未知且样本量较小(通常n<30)时,t分布用于计算均值的置信区间。
2. 假设检验:t检验(包括单样本t检验、独立样本t检验和配对样本t检验)利用t分布来评估两个样本均值之间的差异是否统计显著。这是评估两个群体差异的常用方法。
当然,让我们通过一个简单的例子来说明t分布的应用,特别是在计算置信区间方面。
### 场景
假设你是一名教育研究员,你对高中生在某个标准化测试中的平均成绩感兴趣。你没有整个高中生群体的数据,但你能从中随机抽取一个样本。你抽取了10名学生并得到了以下成绩:85, 92, 88, 74, 78, 91, 88, 82, 79, 85(分数)。
你想要使用这个样本来估计整个高中生群体在该测试中的平均成绩的95%置信区间。由于你没有群体的标准差(总体标准差未知),并且样本量较小(小于30),这是t分布派上用场的完美场景。
### 步骤
1. **计算样本均值(x)**:这是样本成绩的平均值。
2. **计算样本标准偏差(s)**:这是样本成绩的标准偏差。
3. **确定自由度(df)**:自由度等于样本量减一,即 df = n - 1。
4. **选择置信水平(通常是95%)**:确定对应的t值,这个t值基于自由度和所选的置信水平。
5. **计算置信区间**:使用以下公式计算均值的置信区间:
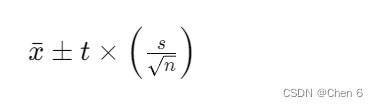
其中,x 是样本均值,t 是根据自由度和置信水平从t分布表中查找的值,s\是样本标准偏差,n是样本大小。
### 示例计算
假设我们已经计算出样本均值为 84.2 分,样本标准偏差为 6.3 分,样本量 \(n=10\),因此自由度 \(df=9\)。对于95%的置信水平,假设我们从t分布表中查到的t值约为2.262(具体值依赖于表)。
置信区间计算如下:
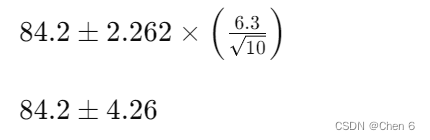
因此,我们估计整个高中生群体在该测试中的平均成绩的95%置信区间大约在79.94到88.46分之间。
### 总结
通过这个例子,我们可以看到t分布在样本量较小且总体标准差未知时,如何帮助我们估计总体参数(如均值)的置信区间。这种方法在实际研究中非常有用,特别是当处理有限的样本数据时。





















 5万+
5万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








