文章目录
Ch12. 无穷级数
零、无穷级数的分类
(1)常数项级数:
①同号级数:正项级数、负项级数
②变号级数:交错级数、任意项级数
(2)函数项级数:
①幂级数
②三角级数:傅里叶级数
一、常数项级数

(一) 级数的概念与性质
1.级数的概念

(1)级数的部分和 S n = ∑ k = 1 n u k S_n=\sum\limits_{k=1}^nu_k Sn=k=1∑nuk:级数的前n项和
级数的前 n n n 项和 称为 级数的部分和: S n = u 1 + u 2 + . . . + u k + . . . + u n = ∑ k = 1 n u k S_n=u_1+u_2+...+u_k+...+u_n=\sum\limits_{k=1}^nu_k Sn=u1+u2+...+uk+...+un=k=1∑nuk
(2)无穷级数: ∑ k = 1 ∞ u k = lim n → ∞ ∑ k = 1 n u k = lim n → ∞ S n \sum\limits_{k=1}^∞u_k=\lim\limits_{n→∞}\sum\limits_{k=1}^nu_k=\lim\limits_{n→∞}S_n k=1∑∞uk=n→∞limk=1∑nuk=n→∞limSn
(常数项)无穷级数,简称(常数项)级数,记为
∑
k
=
1
∞
u
k
\sum\limits_{k=1}^∞u_k
k=1∑∞uk:
∑
k
=
1
∞
u
k
=
u
1
+
u
2
+
.
.
.
+
u
k
+
.
.
.
+
u
n
+
.
.
.
=
lim
n
→
∞
∑
k
=
1
n
u
k
=
lim
n
→
∞
S
n
\sum\limits_{k=1}^∞u_k=u_1+u_2+...+u_k+...+u_n+...=\lim\limits_{n→∞}\sum\limits_{k=1}^nu_k=\lim\limits_{n→∞}S_n
k=1∑∞uk=u1+u2+...+uk+...+un+...=n→∞limk=1∑nuk=n→∞limSn
第 n n n项 u n u_n un 称为级数的一般项
(3)收敛与发散
(1)如果级数 ∑ i = 1 ∞ u i \sum\limits_{i=1}^∞u_i i=1∑∞ui 的部分和数列 { s n } \{s_n\} {sn}有极限s,即 lim n → ∞ s n = s \lim\limits_{n→∞}s_n=s n→∞limsn=s,那么称无穷级数 ∑ i = 1 ∞ u i \sum\limits_{i=1}^∞u_i i=1∑∞ui 收敛。这时极限 s s s叫做这级数的和,并写成 s = u 1 + u 2 + . . . + u i + . . . s=u_1+u_2+...+u_i+... s=u1+u2+...+ui+...
(2))如果级数 ∑ i = 1 ∞ u i \sum\limits_{i=1}^∞u_i i=1∑∞ui 的部分和数列 { s n } \{s_n\} {sn}没有极限,那么称无穷级数 ∑ i = 1 ∞ u i \sum\limits_{i=1}^∞u_i i=1∑∞ui 发散。
例题1:24李林六(二)12. 无穷级数的定义:前n项和的极限
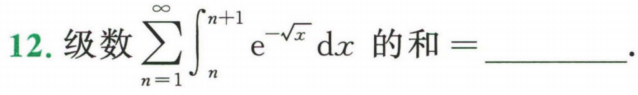
分析:
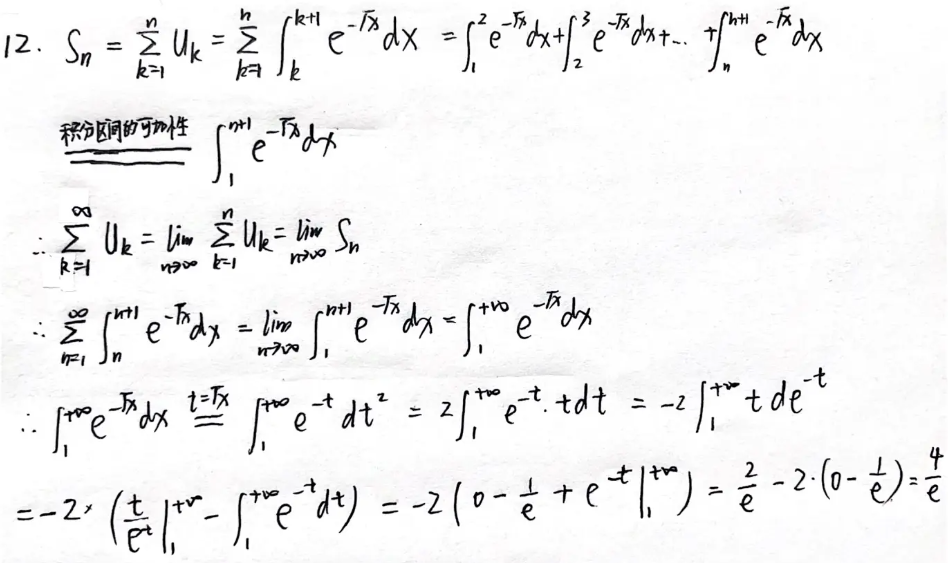
答案: 4 e \dfrac{4}{e} e4
例题2:19年17. 定积分的几何应用:求平面图形的面积、级数求和
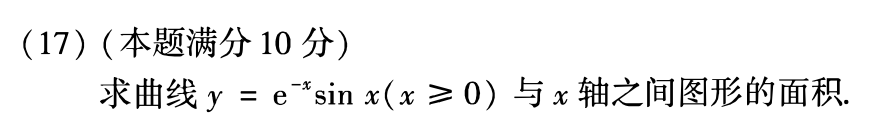
分析:见李艳芳解析

答案: 1 2 + 1 e π − 1 = e π + 1 2 ( e π − 1 ) \dfrac{1}{2}+\dfrac{1}{e^π-1}=\dfrac{e^π+1}{2(e^π-1)} 21+eπ−11=2(eπ−1)eπ+1
例题3:880 P46 二(3)(4)(6)
lim
n
→
∞
∑
k
=
1
n
=
∑
k
=
1
∞
\lim\limits_{n→∞}\sum\limits_{k=1}^n=\sum\limits_{k=1}^∞
n→∞limk=1∑n=k=1∑∞
例题4:用级数的概念判别敛散性(可以写成前n项和的形式)

答案:

 ___
___
2.级数的性质 (5条)


(1)数乘
(2)加减
①收敛 ± 收敛 = 收敛
②收敛 ± 发散 = 发散
③发散 ± 发散 = 不确定
(3)去掉有限项,不改变敛散性
推论:
∑
n
=
1
∞
u
n
\sum\limits_{n=1}^∞u_n
n=1∑∞un收敛,则
∑
n
=
1
∞
u
n
+
1
\sum\limits_{n=1}^∞u_{n+1}
n=1∑∞un+1也收敛
证明:
∑
n
=
1
∞
u
n
+
1
=
∑
n
=
2
∞
u
n
=
∑
n
=
1
∞
u
n
+
1
−
u
1
\sum\limits_{n=1}^∞u_{n+1}=\sum\limits_{n=2}^∞u_n=\sum\limits_{n=1}^∞u_{n+1}-u_1
n=1∑∞un+1=n=2∑∞un=n=1∑∞un+1−u1,收敛
(4)收敛级数任意加括号,仍收敛

(5)必要条件:一般项趋于0

反例: u n = 1 n u_n=\dfrac{1}{n} un=n1
3.四个特殊的常数项级数
①等比级数 / 几何级数
等比级数(几何级数): ∑ n = 0 ∞ a q n = { a 1 − q ( 收敛 ) , ∣ q ∣ < 1 ∞ ( 发散 ) , ∣ q ∣ ≥ 1 \sum\limits_{n=0}^∞aq^n=\left\{\begin{aligned} \dfrac{a}{1-q}\ (收敛),& |q|<1\\ ∞\ (发散),& |q|≥1 \end{aligned}\right. n=0∑∞aqn=⎩ ⎨ ⎧1−qa (收敛),∞ (发散),∣q∣<1∣q∣≥1
例: s 1 ( x ) = ∑ n = 1 ∞ e − n x s_1(x)=\sum\limits_{n=1}^∞e^{-nx} s1(x)=n=1∑∞e−nx。当 ∣ e − x ∣ < 1 |e^{-x}|<1 ∣e−x∣<1,即 x > 0 x>0 x>0 时,由几何级数的求和公式可得 s 1 ( x ) = e − x 1 − e − x = 1 e x − 1 s_1(x)=\dfrac{e^{-x}}{1-e^{-x}}=\dfrac{1}{e^x-1} s1(x)=1−e−xe−x=ex−11。该级数收敛, s 1 ( x ) s_1(x) s1(x)的收敛域为 ( 0 , + ∞ ) (0,+∞) (0,+∞) 【21年18.】
②p级数
p级数: ∑ n = 1 ∞ 1 n p \sum\limits_{n=1}^∞\dfrac{1}{n^p} n=1∑∞np1 { p > 1 ,收敛 0 < p ≤ 1 ,发散 \left\{\begin{aligned} p>1&,收敛 \\ 0<p≤1 &,发散 \end{aligned}\right. {p>10<p≤1,收敛,发散
p=2时, ∑ n = 1 ∞ 1 n 2 = π 2 6 \sum\limits_{n=1}^∞\dfrac{1}{n^2}=\dfrac{π^2}{6} n=1∑∞n21=6π2
③调和级数
调和级数: ∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + . . . + 1 n + . . . = ∞ \sum\limits_{n=1}^∞\dfrac{1}{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{n}+...=∞ n=1∑∞n1=1+21+31+...+n1+...=∞ 发散
④交错调和级数、交错p级数
交错调和级数: ∑ n = 1 ∞ ( − 1 ) n − 1 1 n = 1 − 1 2 + 1 3 + . . . + ( − 1 ) n − 1 1 n + . . . = ln 2 \sum\limits_{n=1}^∞(-1)^{n-1}\dfrac{1}{n}=1-\dfrac{1}{2}+\dfrac{1}{3}+...+(-1)^{n-1}\dfrac{1}{n}+...=\ln2 n=1∑∞(−1)n−1n1=1−21+31+...+(−1)n−1n1+...=ln2 收敛
交错p级数: ∑ n = 1 ∞ ( − 1 ) n − 1 1 n p \sum\limits_{n=1}^∞(-1)^{n-1}\dfrac{1}{n^p} n=1∑∞(−1)n−1np1 { p > 1 , 绝对收敛 0 < p ≤ 1 , 条件收敛 p < 0 , 发散 \left\{\begin{aligned} p>1, & 绝对收敛 \\ 0<p≤1, & 条件收敛 \\ p<0,&发散 \end{aligned}\right. ⎩ ⎨ ⎧p>1,0<p≤1,p<0,绝对收敛条件收敛发散
4.例题:常数项级数 敛散性的判定
1.常用于举反例的一般项:
①
a
n
=
1
n
a_n=\dfrac{1}{n}
an=n1 或
a
n
=
(
−
1
)
n
⋅
1
n
a_n=(-1)^n·\dfrac{1}{n}
an=(−1)n⋅n1
②
a
n
=
(
−
1
)
n
⋅
1
n
a_n=(-1)^n·\dfrac{1}{\sqrt{n}}
an=(−1)n⋅n1
③
u
n
=
0
,
v
n
=
±
1
u_n=0,v_n=±1
un=0,vn=±1
例题1:06年9.

答案:D
例题2:09年4. 常数项级数敛散性的判定

分析:
方法一:排除法
A.反例:
a
n
=
(
−
1
)
n
1
n
a_n=(-1)^n\dfrac{1}{\sqrt{n}}
an=(−1)nn1,
b
n
=
(
−
1
)
n
1
n
b_n=(-1)^n\dfrac{1}{\sqrt{n}}
bn=(−1)nn1,
a
n
b
n
=
1
n
a_nb_n=\dfrac{1}{n}
anbn=n1,级数发散
B.反例:
a
n
=
1
n
a_n=\dfrac{1}{n}
an=n1,
b
n
=
1
n
b_n=\dfrac{1}{n}
bn=n1,
a
n
b
n
=
1
n
2
a_nb_n=\dfrac{1}{n^2}
anbn=n21,级数收敛
D.反例:
a
n
=
1
n
a_n=\dfrac{1}{n}
an=n1,
b
n
=
(
−
1
)
n
1
n
b_n=(-1)^n\dfrac{1}{n}
bn=(−1)nn1,
a
n
b
n
=
1
n
4
a_nb_n=\dfrac{1}{n^4}
anbn=n41,级数收敛
方法二:直接法
①基本结论:对于一般级数
∑
n
=
1
∞
∣
b
n
∣
\sum\limits_{n=1}^∞|b_n|
n=1∑∞∣bn∣收敛,则
∑
n
=
1
∞
b
n
2
\sum\limits_{n=1}^∞b^2_n
n=1∑∞bn2收敛
②∵
lim
n
→
∞
a
n
=
0
\lim\limits_{n→∞}a_n=0
n→∞liman=0,收敛数列必有界,则
∣
a
n
∣
≤
M
|a_n|≤M
∣an∣≤M,则
a
n
2
b
n
2
≤
M
2
b
n
2
a_n^2b_n^2≤M^2b_n^2
an2bn2≤M2bn2
③∵
∑
n
=
1
∞
M
2
b
n
2
\sum\limits_{n=1}^∞M^2b^2_n
n=1∑∞M2bn2收敛,由正项级数的比较审敛法知
∑
n
=
1
∞
a
n
2
b
n
2
\sum\limits_{n=1}^∞a_n^2b^2_n
n=1∑∞an2bn2也收敛
答案:C
例题3:19年3. 常数项级数敛散性的判定

分析:
方法一:排除法:举反例:单调增加的有界数列,可取
u
n
=
−
1
n
u_n=-\dfrac{1}{n}
un=−n1
A.反例:
u
n
=
−
1
n
+
1
u_n=-\dfrac{1}{n}+1
un=−n1+1,则
u
n
n
=
−
1
n
2
+
1
n
\dfrac{u_n}{n}=-\dfrac{1}{n^2}+\dfrac{1}{n}
nun=−n21+n1,发散
B.反例:
u
n
=
−
1
n
u_n=-\dfrac{1}{n}
un=−n1,则
(
−
1
)
n
1
u
n
=
(
−
1
)
n
+
1
n
(-1)^n\dfrac{1}{u_n}=(-1)^{n+1}n
(−1)nun1=(−1)n+1n,发散
C.反例:
u
n
=
−
1
n
u_n=-\dfrac{1}{n}
un=−n1,则
(
1
−
u
n
u
n
+
1
)
=
−
1
n
(1-\dfrac{u_n}{u_{n+1}})=-\dfrac{1}{n}
(1−un+1un)=−n1,发散
方法二:直接法
设
lim
n
→
∞
u
n
=
A
\lim\limits_{n→∞}u_n=A
n→∞limun=A,则
lim
n
→
∞
u
n
2
=
A
2
\lim\limits_{n→∞}u_n^2=A^2
n→∞limun2=A2
∑
k
=
1
n
(
u
k
+
1
2
−
u
k
2
)
=
u
n
+
1
2
−
u
1
2
\sum\limits_{k=1}^n(u_{k+1}^2-u_k^2)=u_{n+1}^2-u_1^2
k=1∑n(uk+12−uk2)=un+12−u12
所以
∑
n
=
1
∞
(
u
n
+
1
2
−
u
n
2
)
=
lim
n
→
∞
∑
k
=
1
n
(
u
k
+
1
2
−
u
k
2
)
=
lim
n
→
∞
(
u
n
+
1
2
−
u
1
2
)
=
A
2
−
u
1
2
\sum\limits_{n=1}^∞(u_{n+1}^2-u_n^2)=\lim\limits_{n→∞}\sum\limits_{k=1}^n(u_{k+1}^2-u_k^2)=\lim\limits_{n→∞}(u_{n+1}^2-u_1^2)=A^2-u_1^2
n=1∑∞(un+12−un2)=n→∞limk=1∑n(uk+12−uk2)=n→∞lim(un+12−u12)=A2−u12
答案:D
例题4:24李林六(一)3.

答案:D
(二) 常数项级数的审敛准则
1.正项级数

(0)正项级数收敛的充分必要条件
正项级数收敛的充分必要条件:它的部分和数列
s
n
{s_n}
sn有上界,即:
①若
∑
n
=
1
∞
u
n
\sum\limits_{n=1}^∞u_n
n=1∑∞un为正项级数且收敛,则
lim
n
→
∞
S
n
\lim\limits_{n→∞}S_n
n→∞limSn存在
②若正项级数
∑
n
=
1
∞
u
n
\sum\limits_{n=1}^∞u_n
n=1∑∞un发散,则
lim
n
→
∞
S
n
\lim\limits_{n→∞}S_n
n→∞limSn不存在
(1)比较判别法
比较审敛法:大的收敛,小的收敛;小的发散,大的发散

1.先预判敛散性。若收敛,要放大。若发散,要缩小。
2.比较审敛法可用于抽象级数的审敛。而极限审敛法、比值法、根值法 必须要有具体的级数表达式才能使用。
结论:抽象级数的审敛,仅能使用比较审敛法。关键是要找到比较的对象。
(2)比较审敛法极限形式

(3)比值法

ρ = lim n → ∞ u n + 1 ( x ) u n ( x ) { 收敛, ρ < 1 发散, ρ > 1 不一定, ρ = 1 (可能收敛,可能发散) ρ=\lim\limits_{n→∞}\dfrac{u_{n+1}(x)}{u_n(x)} \qquad \qquad \left\{\begin{aligned} 收敛,&ρ < 1 \\ 发散,&ρ > 1 \\ 不一定,&ρ =1 (可能收敛,可能发散) \end{aligned}\right. ρ=n→∞limun(x)un+1(x)⎩ ⎨ ⎧收敛,发散,不一定,ρ<1ρ>1ρ=1(可能收敛,可能发散)
(4)根值法

(5)积分判别法

f(x) 单调减、非负、连续
里面的1可以换成任意正整数,如f(x)在[2,+∞]上单减、非负、连续,且an=f(n),则 ∑ n = 2 ∞ a n 与 ∫ 2 + ∞ f ( x ) d x 同敛散 \sum\limits_{n=2}^∞a_n与\int_2^{+∞}f(x)dx同敛散 n=2∑∞an与∫2+∞f(x)dx同敛散
2021考研数学大纲新增——积分判别法。 考研不以任何一本书或教材作为依据,而是以考研大纲作为依据。
适用积分判别法级数: ∑ n = 1 ∞ 1 n p \sum\limits_{n=1}^∞\dfrac{1}{n^p} n=1∑∞np1、 ∑ n = 2 ∞ 1 n ln p n \sum\limits_{n=2}^∞\dfrac{1}{n\ln^pn} n=2∑∞nlnpn1
结论:

5个判别法的选择原则
(1)(2) 比较法、比较法的极限形式
(3)(4) 比值法、根值法
(5) 积分判别法:单调减、非负、连续
| 比较法、比较法的极限形式 | 比值法、根值法 | |
|---|---|---|
| 优点 | 适用范围广 | 使用方便,只需要跟自己比 |
| 缺点 | 使用不方便,需要找一个比较对象 | 适用范围窄,很多做不出判定 |
| 举例 | n p n^p np、 ln n \ln n lnn | 级数通项三巨头: a n a^n an、 n ! n! n!、 n n n^n nn |
先考虑比值法、根值法,若无法做出判定,再考虑比较法、比较法的极限形式
n ! n! n! 用比值法, ( ) n ()^n ()n 用根值法
(6)正项级数收敛结论
(1)若正项级数 ∑ n = 1 ∞ a n \sum\limits_{n=1}^∞a_n n=1∑∞an收敛,则 ∑ n = 1 ∞ a 2 n \sum\limits_{n=1}^∞a_{2n} n=1∑∞a2n、 ∑ n = 1 ∞ a 2 n − 1 \sum\limits_{n=1}^∞a_{2n-1} n=1∑∞a2n−1均收敛。但对一般级数,该结论不成立
(2)①若正项级数
∑
n
=
1
∞
a
n
\sum\limits_{n=1}^∞a_n
n=1∑∞an收敛,则
∑
n
=
1
∞
a
n
2
\sum\limits_{n=1}^∞a^2_n
n=1∑∞an2、
∑
n
=
1
∞
a
n
a
n
+
1
\sum\limits_{n=1}^∞a_na_{n+1}
n=1∑∞anan+1均收敛。
【但对一般级数,该结论不成立。反例:
a
n
=
(
−
1
)
n
1
n
a_n=(-1)^n\dfrac{1}{\sqrt{n}}
an=(−1)nn1,级数收敛。而
a
n
2
=
1
n
a_n^2=\dfrac{1}{n}
an2=n1,级数发散。】
②对于一般级数
∑
n
=
1
∞
∣
a
n
∣
\sum\limits_{n=1}^∞|a_n|
n=1∑∞∣an∣收敛,则
∑
n
=
1
∞
a
n
2
\sum\limits_{n=1}^∞a^2_n
n=1∑∞an2收敛
(3)若正项级数 ∑ n = 1 ∞ a n \sum\limits_{n=1}^∞a_n n=1∑∞an收敛,则 ∑ n = 1 ∞ a n S n \sum\limits_{n=1}^∞a_nS_n n=1∑∞anSn、 ∑ n = 1 ∞ a n S n \sum\limits_{n=1}^∞\dfrac{a_n}{S_n} n=1∑∞Snan均收敛
例题1:22年14.

分析:

答案:-1
2.交错级数: ∑ n = 1 ∞ ( − 1 ) n − 1 u n , u n > 0 \sum\limits_{n=1}^∞(-1)^{n-1}u_n,u_n>0 n=1∑∞(−1)n−1un,un>0
交错级数审敛法——莱布尼茨收敛定理
莱布尼茨收敛定理:【充分非必要条件.反之交错级数收敛,推不出单调减少】
①
u
n
u_n
un单调减少:如
u
n
≥
u
n
+
1
>
0
u_n≥u_{n+1}>0
un≥un+1>0
②
lim
n
→
∞
u
n
=
0
\lim\limits_{n→∞}u_n=0
n→∞limun=0:趋于0
则交错级数
∑
n
=
1
∞
(
−
1
)
n
−
1
u
n
\sum\limits_{n=1}^∞(-1)^{n-1}u_n
n=1∑∞(−1)n−1un (或
∑
n
=
1
∞
(
−
1
)
n
u
n
\sum\limits_{n=1}^∞(-1)^nu_n
n=1∑∞(−1)nun) 收敛
3.任意项级数
(1)绝对收敛与条件收敛

绝对收敛:
∑
n
=
1
∞
u
n
收敛,
∑
n
=
1
∞
∣
u
n
∣
也收敛
绝对收敛:\sum\limits_{n=1}^∞u_n收敛,\sum\limits_{n=1}^∞|u_n|也收敛
绝对收敛:n=1∑∞un收敛,n=1∑∞∣un∣也收敛(本身收敛,各项加绝对值也收敛)
条件收敛:
∑
n
=
1
∞
u
n
收敛,
∑
n
=
1
∞
∣
u
n
∣
发散
条件收敛:\sum\limits_{n=1}^∞u_n收敛,\sum\limits_{n=1}^∞|u_n|发散
条件收敛:n=1∑∞un收敛,n=1∑∞∣un∣发散(本身收敛,各项加绝对值发散)
1.级数共有绝对收敛、条件收敛和发散三种情况。收敛级数只有绝对收敛和条件收敛两种情况。
2.
∑
n
=
1
∞
a
n
x
n
在
x
=
x
0
处条件收敛,则收敛半径
R
=
x
0
\sum\limits_{n=1}^∞a_nx_n在x=x_0处条件收敛,则收敛半径R=x_0
n=1∑∞anxn在x=x0处条件收敛,则收敛半径R=x0
(2)绝对收敛必收敛 (任意项级数)
收敛分绝对收敛和条件收敛: ∑ n = 1 ∞ u n \sum\limits_{n=1}^∞u_n n=1∑∞un绝对收敛 ⇦⇨ ∑ n = 1 ∞ u n \sum\limits_{n=1}^∞u_n n=1∑∞un收敛 且 ∑ n = 1 ∞ ∣ u n ∣ \sum\limits_{n=1}^∞|u_n| n=1∑∞∣un∣也收敛
(3)结论
1.用比值法、根值法,求得绝对值级数发散,则原级数也发散。
2.绝对收敛 ± 条件收敛 = 条件收敛
条件收敛 ± 条件收敛 = 条件收敛 或 绝对收敛
绝对收敛 ± 绝对收敛 = 绝对收敛
(4)例题
例题1:23年4.

答案:A
二、幂级数

幂级数定义: ∑ n = 0 ∞ a n x n = a 0 + a 1 x + a 2 x 2 2 + a 3 x 3 + . . . + a n x n + . . . \sum\limits_{n=0}^∞a_nx^n=a_0+a_1x+a_2x^22+a_3x^3+...+a_nx^n+... n=0∑∞anxn=a0+a1x+a2x22+a3x3+...+anxn+...
例题1:10年14. 数字特征与幂级数

答案:2
(一) 收敛半径、收敛区间、收敛域
1.阿贝尔定理

阿贝尔定理推论:
1.正数R称为幂级数的收敛半径。开区间(-R,R)称为幂级数的收敛区间。
①当|x|<R时,幂级数绝对收敛;
②当|x|>R时,幂级数发散;
③当x = R或x = -R时,幂级数敛散性不定,可能收敛也可能发散。敛散性视
{
a
n
}
\{a_n\}
{an}确定。
2.幂级数 ∑ n = 0 ∞ a n x n \sum\limits_{n=0}^∞a_nx^n n=0∑∞anxn,当且仅当 x = ± R x=±R x=±R 时,才会出现条件收敛。
① ∑ n = 0 ∞ ( − 1 ) n a n \sum\limits_{n=0}^∞(-1)^na_n n=0∑∞(−1)nan条件收敛 ⇦⇨ ∑ n = 0 ∞ a n x n \sum\limits_{n=0}^∞a_nx^n n=0∑∞anxn在 x = − 1 x=-1 x=−1 处条件收敛 ∴ R = 1 R=1 R=1
例题1:15年3. 阿贝尔定理

分析:

答案:B
例题2:24李林六(二)3. 阿贝尔定理

分析:

答案:D
例题3:11年2. 阿贝尔定理 + 莱布尼茨收敛定理
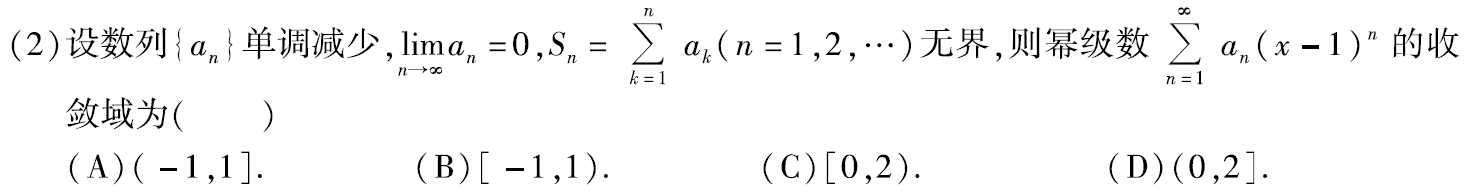
分析:

答案:C
例题4:20年4.

答案:A
2.求幂级数的收敛半径、收敛区间、收敛域
求收敛域:①求收敛半径 ②判断端点是否收敛
(1)阿达玛公式
1.收敛半径R:
①
ρ
=
lim
n
→
∞
∣
a
n
+
1
a
n
∣
R
=
1
ρ
②
ρ
=
lim
n
→
∞
∣
a
n
∣
n
R
=
1
ρ
① \ ρ=\lim\limits_{n→∞}|\dfrac{a_{n+1}}{a_n}|\qquad \qquad R=\dfrac{1}{ρ}\\[3mm]②\ ρ=\lim\limits_{n→∞}\sqrt[n]{|a_n|}\qquad \qquad R=\dfrac{1}{ρ}
① ρ=n→∞lim∣anan+1∣R=ρ1② ρ=n→∞limn∣an∣R=ρ1
2.收敛区间:
(
−
R
,
R
)
(-R,R)
(−R,R) 收敛区间是开区间
3.收敛域:在收敛区间的基础上,验证x=R和x=-R两个端点
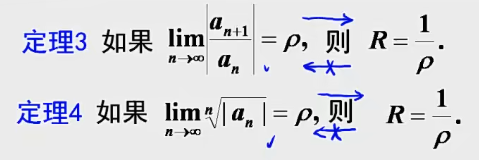

(2)比值法:求幂级数的收敛域
u n ( x ) = a n x n , ρ = lim n → ∞ ∣ u n + 1 ( x ) u n ( x ) ∣ < 1 ,收敛 u_n(x)=a_nx^n,ρ=\lim\limits_{n→∞}|\dfrac{u_{n+1}(x)}{u_n(x)}|<1,收敛 un(x)=anxn,ρ=n→∞lim∣un(x)un+1(x)∣<1,收敛
例题1:22年14. 求函数项级数的收敛域:比值法

分析: e − n x e^{-nx} e−nx,无法完全分离出 a n a_n an,不能使用阿达玛公式,改用比值法(ρ<1)求x的收敛范围

答案:-1
(3)缺项幂级数
①用 比值法 或 根值法,带 u n ( x ) u_n(x) un(x)
缺项幂级数求收敛域: u n ( x ) u_n(x) un(x)比值法 或 根值法,ρ(x)<1,得出收敛区间。再代入端点值验证,得出收敛域。
记 u n ( x ) = a n x n , ρ = lim n → ∞ ∣ u n + 1 ( x ) u n ( x ) ∣ u_n(x)=a_nx^n,ρ=\lim\limits_{n→∞}|\dfrac{u_{n+1}(x)}{u_n(x)}| un(x)=anxn,ρ=n→∞lim∣un(x)un+1(x)∣
②公式改进: R 2 = 1 ρ R^2=\dfrac{1}{ρ} R2=ρ1 (仅能用于选填)
只有偶次项
x
2
n
x^{2n}
x2n 或 奇次项
x
2
n
−
1
x^{2n-1}
x2n−1 的幂级数,
依然用比值法、根值法求ρ,则
R
2
=
1
ρ
R^2=\dfrac{1}{ρ}
R2=ρ1,
R
=
1
ρ
R=\sqrt{\dfrac{1}{ρ}}
R=ρ1

例题1:12年17. 求缺项幂级数的收敛域及和函数

分析:缺项幂级数求收敛域: u n ( x ) u_n(x) un(x)比值法,ρ(x)<1,得出收敛区间。再代入端点值验证,得出收敛域。
答案:

例题2:24李林六(一)19. 求缺项幂级数的收敛域及和函数

答案:

例题3: 1995年4. 缺项幂级数也可以用阿达玛公式,只不过要注意
R
2
=
1
ρ
,
R
=
1
ρ
R^2=\dfrac{1}{ρ},R=\sqrt{\dfrac{1}{ρ}}
R2=ρ1,R=ρ1
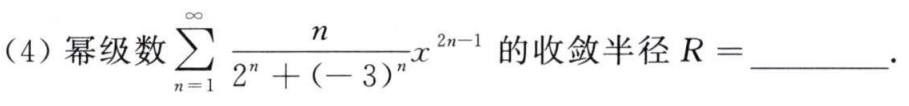
分析:

答案: 3 \sqrt{3} 3
(4)偏心幂级数 ( x − x 0 ) n (x-x_0)^n (x−x0)n
代入收敛半径时:当 x − x 0 = R x-x_0=R x−x0=R、 x − x 0 = − R x-x_0=-R x−x0=−R
(二) 幂级数性质
1.有理运算性质
两个幂级数
∑
n
=
0
∞
a
n
x
n
\sum\limits_{n=0}^∞a_nx_n
n=0∑∞anxn 和
∑
n
=
0
∞
b
n
x
n
\sum\limits_{n=0}^∞b_nx_n
n=0∑∞bnxn 的收敛半径分别为
R
1
R₁
R1和
R
2
R₂
R2,则在
R
=
min
{
R
1
,
R
2
}
R=\min\{R₁,R₂\}
R=min{R1,R2}内,加减乘除运算都成立。
①当
R
1
≠
R
2
R_1≠R_2
R1=R2时,新的收敛半径为R=min{R₁,R₂}
②当
R
1
=
R
2
R_1=R_2
R1=R2时,新的收敛半径R ≥ R1或R2

2.幂级数的和函数S(x)的性质
(1)连续
幂级数 ∑ n = 0 ∞ a n x n \sum\limits_{n=0}^∞a_nx^n n=0∑∞anxn的和函数 S ( x ) S(x) S(x)在其收敛域 I I I 上连续
(2)逐项积分
幂级数
∑
n
=
0
∞
a
n
x
n
\sum\limits_{n=0}^∞a_nx^n
n=0∑∞anxn的和函数
S
(
x
)
S(x)
S(x)在其收敛域
I
I
I上可积,并有逐项积分公式
∫
0
x
S
(
t
)
d
t
=
∫
0
x
∑
n
=
0
∞
a
n
t
n
d
t
=
∑
n
=
0
∞
∫
0
x
a
n
t
n
d
t
=
∑
n
=
0
∞
a
n
n
+
1
x
n
+
1
(
x
∈
I
)
\int_0^xS(t)dt=\int_0^x\sum\limits_{n=0}^∞a_nt^ndt=\sum\limits_{n=0}^∞\int_0^xa_nt^ndt=\sum\limits_{n=0}^∞\dfrac{a_n}{n+1}x^{n+1} \quad (x∈I)
∫0xS(t)dt=∫0xn=0∑∞antndt=n=0∑∞∫0xantndt=n=0∑∞n+1anxn+1(x∈I)。
且逐项积分后所得到的幂级数和原级有相同的收敛半径。
(3)逐项求导: ∑ n = 0 ∞ n x n − 1 = ∑ n = 0 ∞ ( x n ) ′ \sum\limits_{n=0}^∞nx^{n-1}=\sum\limits_{n=0}^∞(x^n)' n=0∑∞nxn−1=n=0∑∞(xn)′
其收敛区间(-R,R)内可导,且有逐项求导公式 S ′ ( x ) = ( ∑ n = 0 ∞ a n x n ) ′ = ∑ n = 0 ∞ ( a n x n ) ′ = ∑ n = 0 ∞ n a n x n − 1 ( ∣ x ∣ < R ) S'(x)=(\sum\limits_{n=0}^∞a_nx^n)'=\sum\limits_{n=0}^∞(a_nx^n)'=\sum\limits_{n=0}^∞na_nx^{n-1} \quad (|x|<R) S′(x)=(n=0∑∞anxn)′=n=0∑∞(anxn)′=n=0∑∞nanxn−1(∣x∣<R)。且逐项求导后所得到的幂级数和原级数有相同的收敛半径。收敛区间上任意阶可导。
① ∑ n = 0 ∞ n x n − 1 = ∑ n = 0 ∞ ( x n ) ′ = ( ∑ n = 0 ∞ x n ) ′ = ( 1 1 − x ) ′ = 1 ( 1 − x ) 2 \sum\limits_{n=0}^∞nx^{n-1}=\sum\limits_{n=0}^∞(x^n)'=(\sum\limits_{n=0}^∞x^n)'=(\dfrac{1}{1-x})'=\dfrac{1}{(1-x)^2} n=0∑∞nxn−1=n=0∑∞(xn)′=(n=0∑∞xn)′=(1−x1)′=(1−x)21
② ∑ n = 1 ∞ n x n − 1 = ∑ n = 1 ∞ ( x n ) ′ = ( ∑ n = 1 ∞ x n ) ′ = ( x 1 − x ) ′ = 1 ( 1 − x ) 2 \sum\limits_{n=1}^∞nx^{n-1}=\sum\limits_{n=1}^∞(x^n)'=(\sum\limits_{n=1}^∞x^n)'=(\dfrac{x}{1-x})'=\dfrac{1}{(1-x)^2} n=1∑∞nxn−1=n=1∑∞(xn)′=(n=1∑∞xn)′=(1−xx)′=(1−x)21
总结:
①幂级数逐项求导有可能缩小收敛域,幂级数逐项积分可能扩大收敛域。但收敛半径、收敛区间不变。
即求导和积分只可能会改变端点处的敛散性。
②要用连续、逐项积分,先求收敛域。要用逐项求导,先求收敛区间。 【2013年16(1)】

(三) 幂级数展开
1.泰勒级数(麦克劳林级数)

| 幂函数 | 展开式 | 级数 |
|---|---|---|
| e x e^x ex | 1 + x + x 2 2 ! + . . . + x n n ! 1+x+\dfrac{x^2}{2!}+...+\dfrac{x^n}{n!} 1+x+2!x2+...+n!xn | ∑ n = 0 ∞ x n n ! ( − ∞ < x < + ∞ ) \sum\limits_{n=0}^∞\dfrac{x^n}{n!}\qquad(-∞<x<+∞) n=0∑∞n!xn(−∞<x<+∞) |
| sin x \sin x sinx | x − x 3 3 ! + x 5 5 ! . . . + ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! + . . . x-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}...+(-1)^{n}\dfrac{x^{2n+1}}{(2n+1)!}+... x−3!x3+5!x5...+(−1)n(2n+1)!x2n+1+... | ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! ( − ∞ < x < + ∞ ) \sum\limits_{n=0}^∞(-1)^{n}\dfrac{x^{2n+1}}{(2n+1)!}\quad(-∞<x<+∞) n=0∑∞(−1)n(2n+1)!x2n+1(−∞<x<+∞) |
| cos x \cos x cosx | 1 − x 2 2 ! + x 4 4 ! . . . + ( − 1 ) n x 2 n ( 2 n ) ! + . . . 1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}...+(-1)^n\dfrac{x^{2n}}{(2n)!}+... 1−2!x2+4!x4...+(−1)n(2n)!x2n+... | ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! ( − ∞ < x < + ∞ ) \sum\limits_{n=0}^∞(-1)^{n}\dfrac{x^{2n}}{(2n)!}\qquad(-∞<x<+∞) n=0∑∞(−1)n(2n)!x2n(−∞<x<+∞) |
| 1 1 − x \dfrac{1}{1-x} 1−x1 | 1 + x + x 2 + . . . + x n + . . . 1+x+x^2+...+x^n+... 1+x+x2+...+xn+... | ∑ n = 0 ∞ x n ( − 1 < x < 1 ) \sum\limits_{n=0}^∞x^n \qquad (-1<x<1) n=0∑∞xn(−1<x<1) |
| 1 1 + x \dfrac{1}{1+x} 1+x1 | 1 − x + x 2 + . . . + ( − 1 ) n x n + . . . 1-x+x^2+...+(-1)^nx^n+... 1−x+x2+...+(−1)nxn+... | ∑ n = 0 ∞ ( − 1 ) n x n ( − 1 < x < 1 ) \sum\limits_{n=0}^∞(-1)^nx^n \qquad (-1<x<1) n=0∑∞(−1)nxn(−1<x<1) |
| ln ( 1 + x ) \ln (1+x) ln(1+x) | x − x 2 2 + x 3 3 + . . . + ( − 1 ) n x n n + . . . x-\dfrac{x^2}{2}+\dfrac{x^3}{3}+...+(-1)^n\dfrac{x^n}{n}+... x−2x2+3x3+...+(−1)nnxn+... | ∑ n = 1 ∞ ( − 1 ) n − 1 x n n ( − 1 < x ≤ 1 ) \sum\limits_{n=1}^∞(-1)^{n-1}\dfrac{x^n}{n}\qquad (-1<x≤1) n=1∑∞(−1)n−1nxn(−1<x≤1) |
| − ln ( 1 − x ) -\ln (1-x) −ln(1−x) | x + x 2 2 + x 3 3 + . . . + x n n + . . . = x+\dfrac{x^2}{2}+\dfrac{x^3}{3}+...+\dfrac{x^n}{n}+...= x+2x2+3x3+...+nxn+...= | ∑ n = 1 ∞ x n n ( − 1 ≤ x < 1 ) \sum\limits_{n=1}^∞\dfrac{x^n}{n}\qquad (-1≤x<1) n=1∑∞nxn(−1≤x<1) |
| arctan x \arctan x arctanx | x − x 3 3 + x 5 5 + . . . + ( − 1 ) n x n n + . . . x-\dfrac{x^3}{3}+\dfrac{x^5}{5}+...+(-1)^n\dfrac{x^n}{n}+... x−3x3+5x5+...+(−1)nnxn+... | ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 ( − 1 ≤ x ≤ 1 ) \sum\limits_{n=0}^∞(-1)^n\dfrac{x^{2n+1}}{2n+1} \qquad(-1≤x≤1) n=0∑∞(−1)n2n+1x2n+1(−1≤x≤1) |
特别的:对于
ln
(
1
+
x
)
\ln(1+x)
ln(1+x),令x=1,可得:
ln
2
=
1
−
1
2
+
1
3
−
1
4
+
.
.
.
\ln2=1-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+...
ln2=1−21+31−41+...
2.函数f(x)展开为幂级数:函数→幂级数
函数→幂级数:
①凑标杆:先求导或积分到标杆
1
1
−
x
\dfrac{1}{1-x}
1−x1 的形式 (x可以为任意形式),以“标杆”为桥梁变成幂级数
∑
n
=
0
∞
x
n
\sum\limits_{n=0}^{∞}x^n
n=0∑∞xn (x可以为任意形式)。
②凑题干:和分两项,尽力合并,注意题干是n=0还是n=1,努力把两项变一项,凑成题干的形式
③求常数项级数:此时的求常数项级数,就是把幂级数中的x代入特定值。
(1)直接展开法

(2)间接展开法
例题1:01年13.

分析:

答案: π 4 − 1 2 \dfrac{π}{4}-\dfrac{1}{2} 4π−21
例题2:

例题3:展开成ln[1+(x-1)],用泰勒级数

例题4:

3.求幂级数的和函数S(x):幂级数→函数
求和函数S(x),先要指出收敛的范围,即求收敛域
(1)换元 凑已知的泰勒级数
例题1:17年12. 积分消分子,凑标杆,再求导回来

分析:
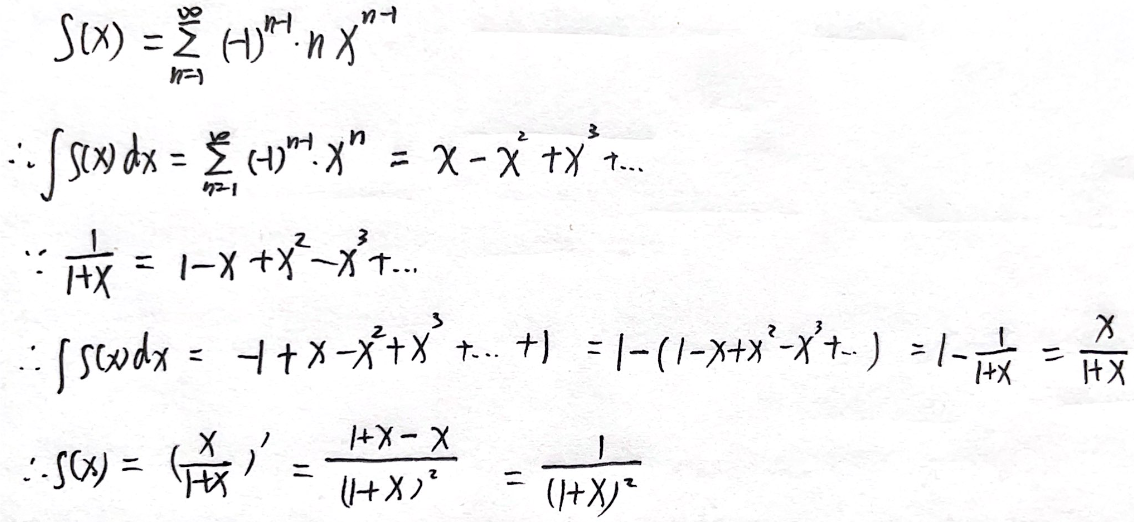
答案: 1 ( 1 + x ) 2 \dfrac{1}{(1+x)²} (1+x)21
例题2:19年11.

分析:凑cosx的泰勒级数
答案: cos x \cos\sqrt{x} cosx
例题3:23李林四(一)14.

分析:换元法
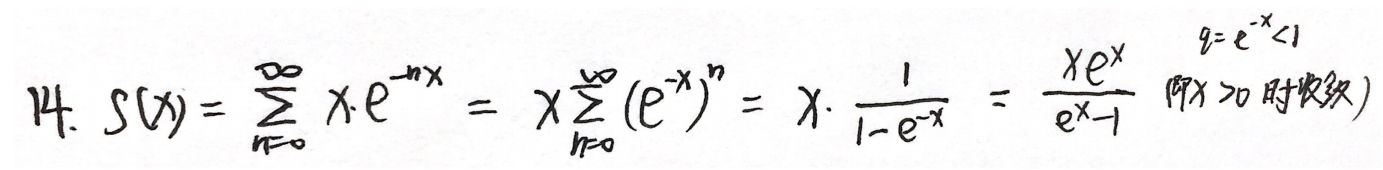
答案:
x
e
x
e
x
−
1
(
x
>
0
)
\dfrac{xe^x}{e^x-1}(x>0)
ex−1xex(x>0)
(2)逐项求导、逐项积分求和函数 S(x)
标杆
(1)重要“标杆”:
∑
n
=
0
∞
x
n
=
1
+
x
+
x
2
+
x
3
+
.
.
.
+
x
n
+
.
.
.
=
1
1
−
x
(
−
1
<
x
<
1
)
\sum\limits_{n=0}^∞x^n=1+x+x²+x³+...+x^n+...=\dfrac{1}{1-x} \qquad (-1<x<1)
n=0∑∞xn=1+x+x2+x3+...+xn+...=1−x1(−1<x<1)
(2)变形:
∑
n
=
1
∞
x
n
=
x
+
x
2
+
x
3
+
.
.
.
+
x
n
+
.
.
.
=
x
1
−
x
(
−
1
<
x
<
1
)
\sum\limits_{n=1}^∞x^n=x+x²+x³+...+x^n+...=\dfrac{x}{1-x} \qquad (-1<x<1)
n=1∑∞xn=x+x2+x3+...+xn+...=1−xx(−1<x<1)
∑ n = 0 ∞ ( − 1 ) n x n = 1 − x + x 2 − x 3 + . . . + ( − 1 ) n x n + . . . = 1 1 + x ( − 1 < x < 1 ) \sum\limits_{n=0}^∞(-1)^nx^n=1-x+x^2-x^3+...+(-1)^nx^n+...=\dfrac{1}{1+x} \qquad (-1<x<1) n=0∑∞(−1)nxn=1−x+x2−x3+...+(−1)nxn+...=1+x1(−1<x<1)
(3)
(4)①有分子就先积分消分子,凑标杆为函数,再求导。
②有分母就先求导消分母,凑标杆为函数,再积分。
一次求导(到凑标杆),对应一次积分。两次求导(到凑标杆),对应两次积分
一次积分(到凑标杆),对应一次求导。两次积分(到凑标杆)。对应两次求导
例题1:看和哪一个公式比较接近。从右向左

例题2:

例题3:

(3)拆两项,分别求
例题1:24李林六(六)13. 构造幂级数求常数项级数、拆两项,分别求

分析:先整理,再换为幂级数代值

答案: 10 9 \dfrac{10}{9} 910
例题2:21年18. 逐项求导,只在开区间(-R,R)上成立,端点值要单独讨论

答案:

例题3:05年16. 求收敛区间、和函数
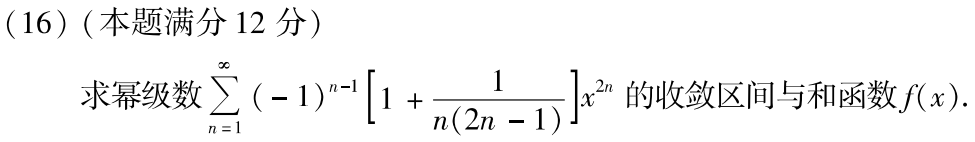
答案:

(4)构造微分方程求和函数 S(x)
含有常数项递推式,求和函数,一般是需要对S(x)求导,构造一阶线性微分方程,利用公式法求解 y=S(x)
例题1:20年17.
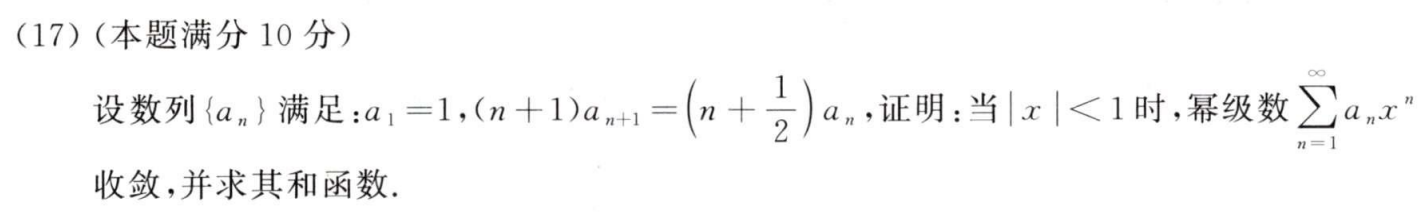
答案:

三、傅里叶级数
形如下式的级数叫做三角级数: a 0 2 + ∑ n = 1 ∞ ( a n cos n π t l ) + b n sin n π t l ) \dfrac{a_0}{2}+\sum\limits_{n=1}^∞(a_n\cos\frac{nπt}{l})+b_n\sin\frac{nπt}{l}) 2a0+n=1∑∞(ancoslnπt)+bnsinlnπt)
令 π t l = x \dfrac{πt}{l}=x lπt=x,三角级数可变为: a 0 2 + ∑ n = 1 ∞ ( a n cos n x ) + b n sin n x ) \dfrac{a_0}{2}+\sum\limits_{n=1}^∞(a_n\cos nx)+b_n\sin nx) 2a0+n=1∑∞(ancosnx)+bnsinnx)
这就把以 2 l 2l 2l 为周期的三角级数转换成以 2 π 2π 2π 为周期的三角级数。
1.傅里叶系数、傅里叶级数
周期为2π的傅里叶系数:
{
a
n
=
1
π
∫
−
π
π
f
(
x
)
cos
n
x
d
x
(
n
=
0
,
1
,
2
,
.
.
.
)
b
n
=
1
π
∫
−
π
π
f
(
x
)
sin
n
x
d
x
(
n
=
1
,
2
,
.
.
.
)
\left\{\begin{aligned} a_n=\frac{1}{π}\int_{-π}^{π}f(x)\cos nx{\rm d}x & \quad (n=0,1,2,...)\\ b_n=\frac{1}{π}\int_{-π}^{π}f(x)\sin nx{\rm d}x & \quad (n=1,2,...) \end{aligned}\right.
⎩
⎨
⎧an=π1∫−ππf(x)cosnxdxbn=π1∫−ππf(x)sinnxdx(n=0,1,2,...)(n=1,2,...)
傅里叶级数: f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) f(x)=\dfrac{a_0}{2}+\sum\limits_{n=1}^∞(a_n\cos nx+b_n\sin nx) f(x)=2a0+n=1∑∞(ancosnx+bnsinnx)
f 1 ( x ) = a 0 2 + a 1 cos x + b 1 sin x f_1(x)=\dfrac{a_0}{2}+a_1\cos x+b_1\sin x f1(x)=2a0+a1cosx+b1sinx
f n ( x ) = a 0 2 + ∑ k = 1 n ( a k cos k x + b k sin k x ) f_n(x)=\dfrac{a_0}{2}+\sum\limits_{k=1}^n(a_k\cos kx+b_k\sin kx) fn(x)=2a0+k=1∑n(akcoskx+bksinkx)
(1)正弦级数、余弦级数
奇函数的傅里叶级数是只含有正弦项的正弦级数: f ( x ) = ∑ n = 1 ∞ b n sin n x f(x)=\sum\limits_{n=1}^∞b_n\sin nx f(x)=n=1∑∞bnsinnx
偶函数的傅里叶级数是只含有余弦项的余弦级数: f ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos n x f(x)=\dfrac{a_0}{2}+\sum\limits_{n=1}^∞a_n\cos nx f(x)=2a0+n=1∑∞ancosnx
证明:
①当 f ( x ) 为奇函数 f(x)为奇函数 f(x)为奇函数时, f ( x ) cos n x f(x)\cos nx f(x)cosnx是奇函数, f ( x ) sin n x f(x)\sin nx f(x)sinnx是偶函数,故
{ a n = 0 ( n = 0 , 1 , 2 , 3 , . . . ) b n = 2 π ∫ 0 π f ( x ) sin n x d x ( n = 1 , 2 , 3 , . . . ) \left\{\begin{aligned} a_n=0 \qquad \qquad \qquad \qquad (n=0,1,2,3,...)\\ b_n=\frac{2}{π}\int_0^{π}f(x)\sin nx{\rm d}x \quad (n=1,2,3,...) \end{aligned}\right. ⎩ ⎨ ⎧an=0(n=0,1,2,3,...)bn=π2∫0πf(x)sinnxdx(n=1,2,3,...)
②当 f ( x ) 为偶函数 f(x)为偶函数 f(x)为偶函数时, f ( x ) cos n x f(x)\cos nx f(x)cosnx是偶函数, f ( x ) sin n x f(x)\sin nx f(x)sinnx是奇函数,故
{ a n = 2 π ∫ 0 π f ( x ) cos n x d x ( n = 0 , 1 , 2 , 3 , . . . ) b n = 0 ( n = 1 , 2 , 3 , . . . ) \left\{\begin{aligned} a_n=\frac{2}{π}\int_0^{π}f(x)\cos nx{\rm d}x \qquad (n=0,1,2,3,...)\\ b_n =0 \qquad \qquad \qquad \qquad \quad \qquad (n=1,2,3,...) \end{aligned}\right. ⎩ ⎨ ⎧an=π2∫0πf(x)cosnxdx(n=0,1,2,3,...)bn=0(n=1,2,3,...)
(2)周期为 2 l 2l 2l的周期函数的傅里叶级数: T = 2 l T=2l T=2l
设周期为
2
l
2l
2l的周期函数
f
(
x
)
f(x)
f(x)满足收敛定理的条件,则它的傅里叶级数展开式为:
f
(
x
)
=
a
0
2
+
∑
n
=
1
∞
(
a
n
cos
n
π
l
x
+
b
n
sin
n
π
l
x
)
f(x)=\dfrac{a_0}{2}+\sum\limits_{n=1}^∞(a_n\cos n\dfrac{π}{l}x+b_n\sin n\dfrac{π}{l}x)
f(x)=2a0+n=1∑∞(ancosnlπx+bnsinnlπx)
其中 { a n = 1 l ∫ − l l f ( x ) cos n π l x d x ( n = 0 , 1 , 2 , . . . ) b n = 1 l ∫ − l l f ( x ) sin n π l x ( n = 1 , 2 , 3 , . . . ) \left\{\begin{aligned} a_n & = \dfrac{1}{l}\int_{-l}^lf(x)\cos n\dfrac{π}{l}xdx \quad (n=0,1,2,...) \\ b_n & =\dfrac{1}{l}\int_{-l}^lf(x)\sin n\dfrac{π}{l}x \quad (n=1,2,3,...) \end{aligned}\right. ⎩ ⎨ ⎧anbn=l1∫−llf(x)cosnlπxdx(n=0,1,2,...)=l1∫−llf(x)sinnlπx(n=1,2,3,...)
当 f ( x ) f(x) f(x)为奇函数时, f ( x ) = ∑ n = 1 ∞ b n sin n π l x f(x)=\sum\limits_{n=1}^∞b_n\sin n\dfrac{π}{l}x f(x)=n=1∑∞bnsinnlπx。其中 b n = 2 l ∫ 0 l f ( x ) sin n π l x b_n=\dfrac{2}{l}\int_0^lf(x)\sin n\dfrac{π}{l}x bn=l2∫0lf(x)sinnlπx
当 f ( x ) f(x) f(x)为偶函数时, f ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos n π l x f(x)=\dfrac{a_0}{2}+\sum\limits_{n=1}^∞a_n\cos n\dfrac{π}{l}x f(x)=2a0+n=1∑∞ancosnlπx。其中 a n = 2 l ∫ 0 l f ( x ) cos n π l x d x a_n=\dfrac{2}{l}\int_0^lf(x)\cos n\dfrac{π}{l}xdx an=l2∫0lf(x)cosnlπxdx
(3)题型1:计算傅里叶系数
例题1:23年13. 计算傅里叶系数:周期为2l的周期函数的傅里叶级数
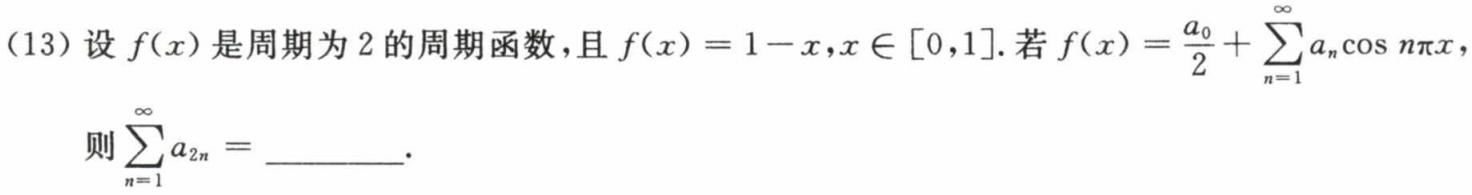
分析:
先求出
a
n
a_n
an,再代入2n,求得
a
2
n
=
0
a_{2n}=0
a2n=0,求和也是0

答案:0
例题2:24李林六(四)14.

分析:定积分平移公式/定积分区间变换公式

答案:0
例题3:03年3.

分析:

答案:1
例题4:1993年3.

分析:

答案: 2 3 π \dfrac{2}{3}π 32π
例题5:14年4.

分析:①傅里叶级数 ②直接计算积分 ③代入选项求积分比最小

答案:A
2.狄利克雷收敛定理

(1)奇延拓
(2)偶延拓
(3)周期延拓
周期延拓:从周期为[-π,π)或(-π,π] 延展为周期为2π的周期函数
(4)题型2:利用狄利克雷收敛定理求值
例题1:13年3. 奇延拓、周期延拓、狄利克雷收敛定理
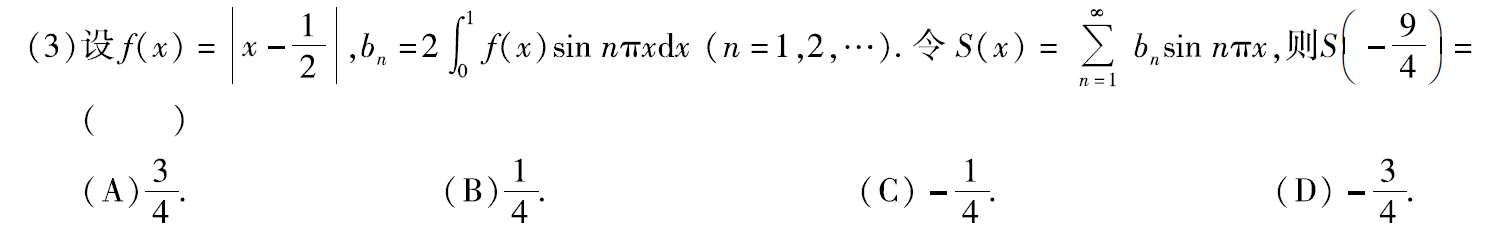
分析:
步骤:关注f(x)、S(x)、bn的范围
①bn是在(0,1),画出f(x)在(0,1)上的图像
②S(x)是正弦级数,是奇函数的傅里叶展开,对f(x)进行奇延拓。再根据周期T=2,对f(x)进行周期延拓。
③根据狄利克雷收敛定理,计算S(x)
S ( − 9 4 ) = S ( − 9 4 + 2 ) = S ( − 1 4 ) = − S ( 1 4 ) = 连续点 狄利克雷收敛定理 − f ( 1 4 ) = − ∣ 1 4 − 1 2 ∣ = − 1 4 S(-\frac{9}{4})=S(-\frac{9}{4}+2)=S(-\frac{1}{4})=-S(\frac{1}{4})\xlongequal[连续点]{狄利克雷收敛定理}-f(\frac{1}{4})=-|\frac{1}{4}-\frac{1}{2}|=-\frac{1}{4} S(−49)=S(−49+2)=S(−41)=−S(41)狄利克雷收敛定理连续点−f(41)=−∣41−21∣=−41

答案:C
例题2:99年选择3 偶延拓、周期延拓

分析:
S(x)是偶函数的傅里叶级数的和函数
画出f(x)图像,把f(x)进行偶延拓、周期延拓,周期为2
S
(
−
5
2
)
=
S
(
−
5
2
+
2
)
=
S
(
−
1
2
)
=
S
(
1
2
)
=
间断点
狄利克雷收敛定理
1
2
+
1
2
=
3
4
S(-\frac{5}{2})=S(-\frac{5}{2}+2)=S(-\frac{1}{2})=S(\frac{1}{2})\xlongequal[间断点]{狄利克雷收敛定理}\dfrac{\frac{1}{2}+1}{2}=\dfrac{3}{4}
S(−25)=S(−25+2)=S(−21)=S(21)狄利克雷收敛定理间断点221+1=43
答案:C
例题3:23李林四(四)14. 周期延拓

分析:

答案: π 2 2 \dfrac{π^2}{2} 2π2
例题4:

分析:展开为正弦,奇延拓
答案:B
3.函数展开为傅里叶级数
(1)周期为 2 π 2π 2π的函数展开
①常规展开:[-π,π]上展开

②奇偶函数:[-π,π]上奇偶函数展开
③半个周期上展开为正弦:奇延拓,展开为余弦:偶延拓
奇延拓:展开为正弦。把(0,π]上的奇函数延展为(-π,π]上的奇函数。
偶延拓:展开为余弦。把(0,π]上的偶函数延展为(-π,π]上的偶函数

(2)周期为 2 l 2l 2l的函数展开
f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n π x l + b n sin n π x l ) f(x)=\dfrac{a_0}{2}+\sum\limits_{n=1}^∞(a_n\cos\dfrac{nπx}{l}+b_n\sin\dfrac{nπx}{l}) f(x)=2a0+n=1∑∞(ancoslnπx+bnsinlnπx)
①常规展开: [ − l , l ] [-l,l] [−l,l]上展开
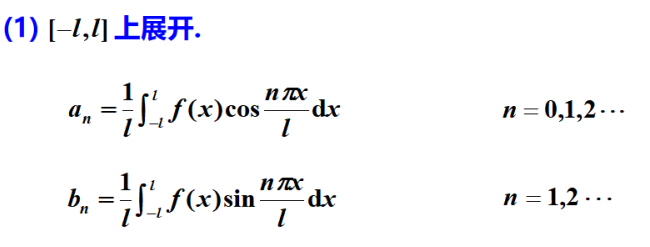
② [ − l , l ] [-l,l] [−l,l]上奇、偶函数的展开
奇函数只有奇数项,只含sin,不含cos
偶函数只有偶数项,只含cos,不含sin

③半个周期上展开为正弦(奇延拓)或展开为余弦(偶延拓):在 [ 0 , l ] [0,l] [0,l]上展开为正弦或展为余弦

(3)题型3:计算傅里叶级数展开式
1.傅里叶级数:
f
(
x
)
=
a
0
2
+
∑
n
=
1
∞
(
a
n
cos
n
x
+
b
n
sin
n
x
)
f(x)=\dfrac{a_0}{2}+\sum\limits_{n=1}^∞(a_n\cos nx+b_n\sin nx)
f(x)=2a0+n=1∑∞(ancosnx+bnsinnx)
2.余弦级数:
偶函数的傅里叶级数是只含有余弦项的余弦级数:
f
(
x
)
=
a
0
2
+
∑
n
=
1
∞
a
n
cos
n
x
f(x)=\dfrac{a_0}{2}+\sum\limits_{n=1}^∞a_n\cos nx
f(x)=2a0+n=1∑∞ancosnx
3.傅里叶系数
周期为2π的傅里叶系数:
{
a
n
=
1
π
∫
−
π
π
f
(
x
)
cos
n
x
d
x
(
n
=
0
,
1
,
2
,
.
.
.
)
b
n
=
1
π
∫
−
π
π
f
(
x
)
sin
n
x
d
x
(
n
=
1
,
2
,
.
.
.
)
\left\{\begin{aligned} a_n=\frac{1}{π}\int_{-π}^{π}f(x)\cos nx{\rm d}x & \quad (n=0,1,2,...)\\ b_n=\frac{1}{π}\int_{-π}^{π}f(x)\sin nx{\rm d}x & \quad (n=1,2,...) \end{aligned}\right.
⎩
⎨
⎧an=π1∫−ππf(x)cosnxdxbn=π1∫−ππf(x)sinnxdx(n=0,1,2,...)(n=1,2,...)
例题1:24李林四(三)12. 将函数展开成傅里叶级数

分析:
偶函数的傅里叶级数是只含有余弦项的余弦级数:
f
(
x
)
=
a
0
2
+
∑
n
=
1
∞
a
n
cos
n
x
f(x)=\dfrac{a_0}{2}+\sum\limits_{n=1}^∞a_n\cos nx
f(x)=2a0+n=1∑∞ancosnx。本题只需要求
a
0
a_0
a0 和
a
n
a_n
an,即本质还是求傅里叶系数
a
n
a_n
an。

答案:
π
+
2
2
+
∑
n
=
1
∞
2
n
2
π
[
(
−
1
)
n
−
1
]
cos
n
x
(
0
≤
x
≤
π
)
\dfrac{π+2}{2}+\sum\limits_{n=1}^∞\dfrac{2}{n^2π}[(-1)^n-1]\cos nx \quad (0≤x≤π)
2π+2+n=1∑∞n2π2[(−1)n−1]cosnx(0≤x≤π)
例题2:95年四((2)

分析:

例题3:91年五

分析:



























 1102
1102

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










