Predictive Uncertainty Estimation via Prior Networks 阅读笔记

Predictive Uncertainty Estimation via Prior Networks 阅读笔记

资源

https://github.com/Jiachen-T-Wang/dirichlet-priornet/blob/master/am207_dpn_paper.ipynb

非常好复现使我佩服。

摘要

不确定性可能来自模型不确定性、数据不确定性、分布不确定性。现有的方法多是通过模型不确定性或者数据不确定性隐式地对分布不确定性建模。**本文提出了先验网络，明确建模了分布不确定性。**在 MNIST 和 CIFAR-10 数据集上识别分布外 (OOD) 样本和检测错误分类的任务中评估 PN，发现它们的性能优于以前的方法。

1 Introduction

现有方法混淆了预测不确定性的不同方面：

1. 模型不确定性或认知不确定性衡量在给定训练数据的情况下估计模型参数的不确定性 - 这衡量模型与数据的匹配程度。随着训练数据规模的增加，模型不确定性可以降低。
2. 数据不确定性或任意不确定性是由于数据的自然复杂性而产生的不可约的不确定性，例如类重叠、标签噪声、同方差和异方差噪声。数据不确定性可以被认为是“已知-未知”——模型理解（知道）数据，并且可以自信地说明给定输入是否难以分类（未知）。
3. 分布不确定性是由于训练和测试分布之间的不匹配（也称为数据集偏移）而产生的——这种情况经常出现在现实世界的问题中。分布不确定性是“未知的未知”——模型不熟悉测试数据，因此无法自信地做出预测。

这项工作通过扩展 [21, 22] 中所做的工作，同时从贝叶斯方法中汲取灵感，解决了对三种类型的预测不确定性的显式预测。

2 Current Approaches to Uncertainty Estimation

$$\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },\mathcal{D}\right)=\int \underset{\text{Data }}{\underbrace{\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)}}\underset{\text{Model }}{\underbrace{\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})}}d\mathbf{\theta }\text{\hspace{1em}(1)}$$

A model’s estimates of data uncertainty are described by the posterior distribution over class labels given a set of model parameters $\theta$ and model uncertainty is described by the posterior distribution over the parameters given the data

Intractable Points:

1. uncertainty in the model parameters induces a distribution over distributions $\mathrm{P}({\omega }_c\mid {\mathbf{x}}^{\ast },\mathbf{\theta })$，
   如何理解分布的分布；注意$\mathrm{P}$和$\mathrm{p}$的区别；$\mathrm{P}$是分布，$\mathrm{p}$是概率密度。
   因此此处的a distribution over distributions $\mathrm{P}({\omega }_c\mid {\mathbf{x}}^{\ast },\mathbf{\theta })$：
   理解为 $\mathrm{P}({\omega }_c\mid {\mathbf{x}}^{\ast },\mathbf{\theta })$作为随机变量，遵循$\mathrm{P}(\mathbf{\theta }\mid \mathcal{D})$。
   所以写作：$\mathrm{P}({\omega }_c\mid {\mathbf{x}}^{\ast },\mathbf{\theta })\sim \mathrm{P}(\mathbf{\theta }\mid \mathcal{D})$。
   注意英文的表达：$分布\text{over}\text{随机变量}$ 。

2. 为了求真实的$\mathrm{P}\left({\omega }_c\mid x^{\ast },\mathcal{D}\right)$。我们需要对$\theta$进行边缘化，但是$\mathrm{P}(\mathbf{\theta }\mid \mathcal{D})$很难获得。因此可以使用变分近似，获得一个$\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})\approx \mathrm{q}(\mathbf{\theta })$

3. 即使得到了变分近似，边缘化/积分也依然困难，因为$\theta$对于参数化的神经网络，难以积分。所以一般使用采样近似，例如：MC Dropout、Langevin Dynamics或者显式的ensembling。$\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },\mathcal{D}\right)\approx \frac{1}{M}{\sum }_{i=1}^M\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },{\mathbf{\theta }}^{(i)}\right),{\mathbf{\theta }}^{(i)}\sim \mathrm{q}(\mathbf{\theta })$

   

   注意这里的表达，非常精炼。集成里面的每个分布$\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },{\mathbf{\theta }}^{(i)}\right)$都是从变分分布中采样得到的；本质是一个类别分布$\mu$，并且以$x$为条件，有$y\sim \mu$；且每个$\mu$都是单纯形上的一个点。（类别分布：

   碎片化学习之数学（二）：Categorical Distribution - 李新春的文章 - 知乎
   https://zhuanlan.zhihu.com/p/59550457

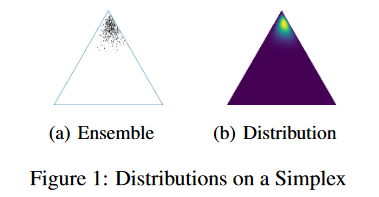
总而言之：涉及到：模型先验、近似模型后验、集成→ID一致，OOD多样化、在单纯形上制作隐式的条件分布（注意这种表达：$在\mathbb{R}域上制作分布\mathcal{P}$）

什么是隐式分布：隐式分布是指无法得到这个分布的PDF，但是可以从分布中进行采样，估计期望和梯度

最后，Cue了一下现有的方法：要么是贝叶斯系列的，先验难假设、后验难近似、即使近似了采样了也开销大；另一套非贝叶斯系列的，只在预测熵层面，鼓励ood高熵、id低熵，开销小，但是没法区分ood和类overlap的数据。

3 Prior Networks

Having described Existing Approaches ,本文提出了预测不确定性的替代方法——先验网络。再次精炼贝叶斯方法：

通过适当选择模型先验和近似推理，construct an implicit conditional distribution over distributions on a simplex with certain desirable attributes
在单纯形上构建一个隐式的条件分布$\mathrm{P}(\mu \mid {\mathbf{x}}^{\ast },\mathbf{\theta })$，在单纯形上=描述单纯形上不同点的概率密度，这里的$\mu$就是代表单纯形上的随机变量。Where $\mathbf{\mu }$ is a vector of probabilities: ${\left[{\mu }_1,\cdots ,{\mu }_K\right]}^T={\left[\mathrm{P}\left(y={\omega }_1\right),\cdots ,\mathrm{P}\left(y={\omega }_K\right)\right]}^T$

我们的方法是直接显式参数化单纯形上的一个分布$\mathrm{P}(\mu \mid {\mathbf{x}}^{\ast },\mathbf{\theta })$，使用先验网络，训练它的行为像贝叶斯方法里面的隐式分布一样，具体看图，三种情况：

先验网络：明确区分数据和分布不确定性：

1. 数据不确定性用点估计类别分布描述
2. 分布不确定性用类别分布上的分布描述（又称单纯形上的分布）

Theoretical Properties of Prior Network

$$\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },\mathcal{D}\right)=\iint \underset{\text{Data }}{\underbrace{\mathrm{p}\left({\omega }_c\mid \mathbf{\mu }\right)}}\underset{\text{Distributional }}{\underbrace{\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)}}\underset{\text{Model }}{\underbrace{\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})}}d\mathbf{\mu }d\mathbf{\theta }\text{\hspace{1em}(3)}$$

类似的结构已经在之前的非神经贝叶斯模型探索了，例如LDA（潜在迪利克雷分配）

David M. Blei, Andrew Y. Ng, and Michael I. Jordan, “Latent Dirichlet Allocation,” Journal of Machine Learning Research, vol. 3, pp. 993–1022, Mar. 2003.

通常会添加额外的不确定性，以提高模型的灵活性，并通过边缘化或抽样来获得预测。

然而，在这项工作中，添加了额外的不确定性水平，以便能够提取额外的不确定性度量，具体取决于模型的边缘化方式。

marginalizing out $\mu$

$$\int \left[\int \mathrm{p}\left({\omega }_c\mid \mathbf{\mu }\right)\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)d\mathbf{\mu }\right]\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})d\mathbf{\theta }=\int \mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})d\mathbf{\theta }\text{\hspace{1em}(4)}$$

Since the distribution over $\mu$ is lost in the marginalization it is unknown how sharp or flat it was around the point estimate.注意这里得到的$\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)$ 是大写的分布；

**性质：**此时如果$\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)$ 是平坦的，不知道是分布不确定性还是数据不确定性。

In this situation, it will be necessary to again rely on measures which assess the spread of an MC ensemble, like mutual information ；此时依赖于：评估MC ensemble传播的度量，e.g. 互信息，来确定不确定性的来源。🤔因此先验网络和过去的贝叶斯/非贝叶斯方法对不确定性的建模是一样的，可以看作是不确定工具箱的额外工具——专门以概率可解释的方法来捕捉分布失配的影响。

marginalizing out $\theta$

$$\int \mathrm{p}\left({\omega }_c\mid \mathbf{\mu }\right)\left[\int \mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})d\mathbf{\theta }\right]d\mathbf{\mu }=\int \mathrm{p}\left({\omega }_c\mid \mathbf{\mu }\right)\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast },\mathcal{D}\right)d\mathbf{\mu }\text{\hspace{1em}(5)}$$

**性质：**这在给定模型不确定性的情况下，产生了数据和分布不确定性的估计。

但是对$\theta$的边缘化，尽管可以MC近似，但是棘手。

本文中假设：给定适当的正则化和训练数据大小的情况下，模型参数$\theta$的点估计就够了。

$$\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})=\delta (\mathbf{\theta }-\hat{\mathbf{\theta }})⟹\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\mathcal{D}\right)\approx \mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\hat{\mathbf{\theta }}\right)\text{\hspace{1em}(6)}$$

Dirichlet Prior Networks

A Prior Network for classification parametrizes a distribution over a simplex, such as a Dirichlet , Mixture of Dirichlet distributions or the Logistic-Normal distribution. In this work the Dirichlet distribution is chosen due to its tractable analytic properties.

A Dirichlet distribution is a prior distribution over categorical distribution, which is parameterized by its concentration parameters $\mathbf{\alpha }$, where ${\alpha }_0$ , the sum of all ${\alpha }_c$ , is called the precision of the Dirichlet distribution. Higher values of ${\alpha }_0$ lead to sharper distributions.

$$\mathrm{Dir}(\mathbf{\mu }\mid \mathbf{\alpha })=\frac{\Gamma \left({\alpha }_0\right)}{{\prod }_{c=1}^K\Gamma \left({\alpha }_c\right)}\prod _{c=1}^K{\mu }_c^{{\alpha }_c-1},{\alpha }_c>0,{\alpha }_0=\sum _{c=1}^K{\alpha }_c\text{\hspace{1em}(7)}$$

A Prior Network which parametrizes a Dirichlet will be referred to as a Dirichlet Prior Network (DPN). A DPN will generate the concentration parameters $\mathbf{\alpha }$ of the Dirichlet distribution.

$$\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\hat{\mathbf{\theta }}\right)=\mathrm{Dir}(\mathbf{\mu }\mid \mathbf{\alpha }),\mathbf{\alpha }=\mathbf{f}\left({\mathbf{x}}^{\ast };\hat{\mathbf{\theta }}\right)\text{\hspace{1em}(8)}$$

The posterior over class labels will be given by the mean of the Dirichlet:
类别标签的后验分布由迪利克雷分布的期望给出：

$$\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast };\hat{\mathbf{\theta }}\right)=\int \mathrm{p}\left({\omega }_c\mid \mathbf{\mu }\right)\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\hat{\mathbf{\theta }}\right)d\mathbf{\mu }=\frac{{\alpha }_c}{{\alpha }_0}\text{\hspace{1em}(9)}$$

If an exponential output function is used for the DPN, where ${\alpha }_c=e^{z_c}$, then the expected posterior probability of a label ${\omega }_c$ is given by the output of the softmax (eq. 10).
如果DPN使用指数输出函数，那么类别标签的期望后验分布等效于softmax给出

$$\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast };\hat{\mathbf{\theta }}\right)=\frac{e^{z_c\left({\mathbf{x}}^{\ast }\right)}}{{\sum }_{k=1}^K{e}^{z_k\left({\mathbf{x}}^{\ast }\right)}}\text{\hspace{1em}(10)}$$

Thus, standard DNNs for classification with a softmax output function can be viewed as predicting the expected categorical distribution under a Dirichlet prior. The mean, however, is insensitive to arbitrary scaling of ${\alpha }_c$ . Thus the precision ${\alpha }_0$, which controls the sharpness of the Dirichlet, is degenerate under standard cross-entropy training. It is necessary to change the cost function to explicitly train a DPN to yield a sharp or flat prior distribution around the expected categorical depending on the input data.

因此标准的带有Softmax的DNN可以看作是预测迪利克雷先验下的类别标签的期望后验分布。
也就是说logit取对数，看作迪利克雷的浓度参数，再取softmax，看作对迪利克雷分布求期望的显式解。

然而，$DNN的e^{logi{t}_c}=Dirichlet的{\alpha }_c$ ，导致标准DNN的输出对Dirichlet分布参数$\alpha$的精确值并不敏感。这里好好理解一下！😢

作者指出，由于标准的交叉熵损失函数并未显式地考虑到Dirichlet分布的参数$\alpha$，因此无法有效地训练模型以产生期望的分类分布。

因此，建议修改损失函数！

Dirichlet Prior Network Training

训练DPN的方法可能有多种，但是本文只研究一种方法：

DPN 以多任务方式进行显式训练，以最小化模型与集中于分布内数据的适当类别的尖锐狄利克雷分布之间以及模型与平坦狄利克雷分布之间的 KL 散度分布外数据

$$\mathcal{L}(\mathbf{\theta })={\mathbb{E}}_{{\mathrm{p}}_{\text{in }}(\mathbf{x})}[KL[\mathrm{Dir}(\mathbf{\mu }\mid \hat{\mathbf{\alpha }})\Vert \mathrm{p}(\mathbf{\mu }\mid \mathbf{x};\mathbf{\theta })]]+{\mathbb{E}}_{{\mathrm{p}}_{\text{out}}(\mathbf{x})}[KL[\mathrm{Dir}(\mathbf{\mu }\mid \tilde{\mathbf{\alpha }})\Vert \mathrm{p}(\mathbf{\mu }\mid \mathbf{x};\mathbf{\theta })]]\text{\hspace{1em}(11)}$$

A flat Dirichlet is chosen as the uncertain distribution in accordance with the principle of insufficient reason [32], as all possible categorical distributions are equiprobable.
根据理由不足原则，选择平坦狄利克雷作为不确定分布[32]，因为所有可能的分类分布都是等概率的。

多任务训练目标的设置

为了使用这个损失函数来训练，必须定义分布内目标$\hat{\mathbf{\alpha }}$ 和 分布外目标 $\tilde{\mathbf{\alpha }}$ ；

1. 分布外目标很好设置，直接设置所有$\widetilde{{\alpha }_c}$为1来指定平坦狄利克雷分布。
2. 分布内目标，重参数化$\widehat{{\mathbf{\alpha }}_{\mathbf{c}}}$为目标精度$\widehat{{\mathbf{\alpha }}_0}$，此外依赖均值${\hat{\mu }}_c=\frac{{\hat{\alpha }}_c}{{\hat{\alpha }}_0}$
   1. $\widehat{{\mathbf{\alpha }}_0}$是训练时设置的超参数，均值是简单的分类独热目标。
   2. 更复杂的是，在定义的 KL 损失下，学习稀疏的“1-hot”连续分布（实际上是 delta 函数）具有挑战性，因为误差表面变得不太适合优化；有2种方法：
      1. 首先，可以平滑目标均值（eq. 12），这将少量概率密度重新分配到狄利克雷的其他角。
      2. 或者，师生训练[33]可用于指定非稀疏目标均值μ。

$${\hat{\mu }}_c=\{\begin{array}{ll}1-(K-1)ϵ& \text{ if }\delta \left(y={\omega }_c\right)=1\\ ϵ& \text{ if }\delta \left(y={\omega }_c\right)=0\end{array}\text{\hspace{1em}(12)}$$

本文中使用了平滑方法。此外，交叉熵可以用作分布数据的辅助损失。

OOD样本的来源

多任务训练目标（等式 11）需要来自域外分布 ${\mathrm{P}}_{\text{out}}$ 的 ̃ $x$ 样本。然而，真正的域外分布未知，并且样本不可用。

1. 一种解决方案是使用生成模型在域内区域的边界上综合生成点[21, 22]。
2. 另一种方法是使用不同的真实数据集作为域外分布的一组样本[22]。

4 Uncertainty Measures

上一节介绍了一个用于建模不确定性的新框架。

本节探讨了在给定训练有素的 DNN、DPN 或贝叶斯 MC 集成的情况下量化不确定性的一系列度量。讨论分为 4 类度量，具体取决于（eq. 3）边缘化的方式。 推导的细节可以在附录C中找到。

$$\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },\mathcal{D}\right)=\iint \underset{\text{Data }}{\underbrace{\mathrm{p}\left({\omega }_c\mid \mathbf{\mu }\right)}}\underset{\text{Distributional }}{\underbrace{\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)}}\underset{\text{Model }}{\underbrace{\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})}}d\mathbf{\mu }d\mathbf{\theta }\text{\hspace{1em}(3)}$$

✨Derive from $\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast };\mathcal{D}\right)$ full marginalization

可以通过MC ensemble或者模型参数的点估计$\hat{\theta }$对公式4进行全边缘化。

probability of the predicted class （max probability）——最大概率

这是对预测中使用的置信度的度量，used in [13, 22, 30, 23, 11].

$$\mathcal{P}=\underset{c}{\max }\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast };\mathcal{D}\right)\text{\hspace{1em}(1-1)}$$

entropy of the predictive distribution （Entropy）——预测熵

类似于最大概率，但是表征了整个预测分布的不确定性。[23, 18, 11]

$$\mathcal{H}\left[\mathrm{P}\left(y\mid x^{\ast };\mathcal{D}\right)\right]=-\sum _{c=1}^K\mathrm{P}\left({\omega }_c\mid x^{\ast };\mathcal{D}\right)\ln \left(\mathrm{P}\left({\omega }_c\mid x^{\ast };\mathcal{D}\right)\right)\text{\hspace{1em}(1-2)}$$

预期分布的最大概率和熵可以被视为预测中总体不确定性的度量。

✨Derive from $\mathrm{P}\left({\omega }_c\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})$ marginalizing out $\mu$

MI between $\theta$ and $y$——$y$ 和 $\theta$ 之间的互信息

分类标签 $y$ 和模型参数 $\theta$ 之间的互信息 (MI) [23] 是集合传播的度量 { P ( ω c ∣ x ∗ , θ ( i ) ) } i = 1 M \{\mathrm{P}\left(\omega_c \mid \boldsymbol{x}^*, \boldsymbol{\theta}^{(i)})\right\}_{i=1}^M {P(ωc​∣x∗,θ(i))}i=1M​[18]，评估了由于模型不确定性而导致的预测不确定性。

因此，MI 隐含地捕捉了分布不确定性的要素。

MI 可以表示为由期望预测分布的熵捕获的总不确定性与由集合中每个成员的熵捕获的期望数据不确定性之间的差异（eq. 16）
（期望预测分布的熵-预测分布熵的期望|以$\theta$求期望）
（$\mathrm{P}\to \mathbb{E}\to \mathcal{H}$
和$\mathrm{P}\to \mathcal{H}\to \mathbb{E}$ 做差；这样反映的就是以 $\theta$ 求期望前后的不确定性差异——反映了模型参数引起的不确定性）

$$\underset{\text{Model Uncertainty }}{\underbrace{\mathcal{I}\left[y,\mathbf{\theta }\mid {\mathbf{x}}^{\ast },\mathcal{D}\right]}}=\underset{\text{Total Uncertainty }}{\underbrace{\mathcal{H}\left[{\mathbb{E}}_{\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})}\left[\mathrm{P}\left(y\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)\right]\right]}}-\underset{\text{Expected Data Uncertainty }}{\underbrace{{\mathbb{E}}_{\mathrm{p}(\mathbf{\theta }\mid \mathcal{D})}\left[\mathcal{H}\left[\mathrm{P}\left(y\mid {\mathbf{x}}^{\ast },\mathbf{\theta }\right)\right]\right]}}\text{\hspace{1em}(2-1)}$$

如何理解：类似方差： $\mathrm{Var}(X)=\mathbb{E}\left[X^2\right]-{\mu }^2$ （方的期望-期望的方）期望的方是均值的发散性，方的期望反映了$X_i$各自发散性的均值；做差就反映了期望前后的发散性差异，也就是$X$内部彼此的差异。

✨Derive from $\mathrm{p}\left({\omega }_c\mid \mathbf{\mu }\right)\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast },\mathcal{D}\right)$ marginalizing out $\theta$

MI between $\mu$ and $y$——$y$ 和 $\mu$ 之间的互信息

此类中的第一个度量是 $y$ 和 $\mu$ 之间的互信息（等式 17），其行为与 $y$ 和 $\theta$ 之间的 MI 完全相同；

但现在的集合传播的度量显然是评估由于分布不确定性导致的预测不确定性。

$$\underset{\text{Distributional Uncertainty }}{\underbrace{\mathcal{I}\left[y,\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\mathcal{D}\right]}}=\underset{\text{Total Uncertainty }}{\underbrace{\mathcal{H}\left[{\mathbb{E}}_{\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\mathcal{D}\right)}[\mathrm{P}(y\mid \mathbf{\mu })]\right]}}-\underset{\text{Expected Data Uncertainty }}{\underbrace{{\mathbb{E}}_{\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\mathcal{D}\right)}[\mathcal{H}[\mathrm{P}(y\mid \mathbf{\mu })]]}}\text{\hspace{1em}(3-2)}$$

differential entropy——微分熵

当所有分类分布都是等概率时（当狄利克雷分布平坦时，即当狄利克雷先验中的样本种类最多时），此度量最大化。微分熵非常适合测量分布不确定性，因为即使狄利克雷先验下的期望分类分布具有高熵，它也可能很低（即使期望预测分类分布$\mathbb{E}(\mu )$是$[0.33,0.33,0.33]$这样的高熵，当多个预测分类分布$\mu$ 都是差不多接近时，微分熵也很低，此时的分布不确定性会小——思考此时如果是ID，在模型训练的不同时期，这个分布不确定性也会越来越小，这里就体现了模型不确定性影响分布不确定性），并且还捕获数据不确定性的元素。（😢这里有点不理解）
大致理解了，就是说微分熵不受数据不确定性的影响，大概？实验部分Table3。

$$\mathcal{H}\left[\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\mathcal{D}\right)\right]=-{\int }_{{\mathcal{S}}^{K-1}}\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\mathcal{D}\right)\ln \left(\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\mathcal{D}\right)\right)d\mathbf{\mu }\text{\hspace{1em}(3-2)}$$

✨Derive from full eq.4 No marginalizing

MI between $\mu$ and $\theta$

评估了集合$\mathrm{p}\left(\mathbf{\mu }\mid {\mathbf{x}}^{\ast };\mathbf{\theta }\right)$ 传播的度量（这里区别于前面的，涉及了2个变量$\mu$ 和$\theta$ ），可以通过贝叶斯集成方法计算。（😢这里有点不理解）

5 Experiments

前面的部分讨论了对预测不确定性的不同方面进行建模，并提出了几种量化不确定性的方法。

本节在两组实验中比较了所提出的方法和以前的方法。

1. 第一个实验说明了 DPN 相对于其他非贝叶斯方法 [22, 30] 在合成数据上的优势
2. 第二组实验评估了 MNIST 和 CIFAR-10 上的 DPN，并将它们与 DNN 和通过 Monte-Carlo Dropout 生成的集成进行比较（MCDP）on the tasks of misclassification detection and out-of-distribution data detection
3. 实验设置在附录 A 中描述，其他实验在附录 B 中描述。

5.1 Synthetic Experiments

创建了一个简单的数据集，其中包含 3 个具有等距均值和束缚各向同性方差 σ 的高斯分布类。当 σ = 1 时，类别不重叠（图 3a）；当 σ = 4 时，类别重叠（图 3d）。

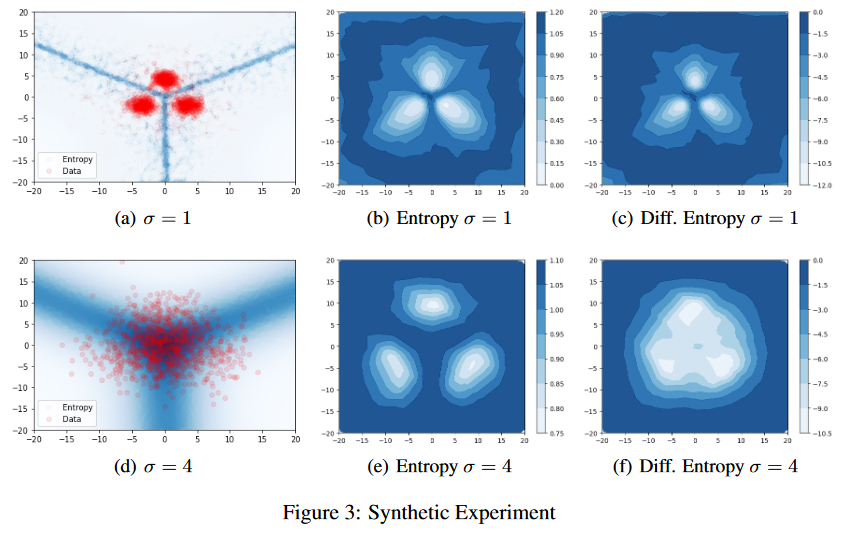
预测分布的熵 vs 微分熵：
在没有OverLap的情况下，OOD|ID都可以分开；
在有OverLap的情况下
Entropy：OverLap&OOD高熵，没法区分ID. OverLap和OOD；
Diff. Entropy : ID低熵，OOD高熵，依然可以分开。

5.2 MNIST and CIFAR-10 Experiments

Run on the MNIST and CIFAR-10 datasets to assess the DPN’s ability to estimate uncertainty.

1. An in-domain misclassification detection experiment
2. An out-of-distribution (OOD) input detection experiment

都是给定一个Uncertainty度量，检测误分类&&检测OOD。正类规定：

1. Misclassifications are chosen as the positive class.
2. Out-of-distribution samples are chosen as the positive class.

OMNIGLOT 数据集 [37] 缩小至 28x28 像素，用作 MNIST 的真实“OOD”数据。随机选择 15000 个 OMNIGLOT 数据样本，形成一组平衡的正样本（OMNIGLOT）和负样本（MNIST 有效+测试）。对于 CIFAR-10，考虑了三个 OOD 数据集 - SVHN、LSUN 和 TinyImagetNet (TIM) [38,39,40]。

所考虑的两种基线方法从 DNN [13] 的类后验或通过应用于同一 DNN [23, 18] 的 MC dropout 生成的集合导出不确定性度量。第 4 节中描述的所有不确定性度量都针对这两项任务进行了探索，以便了解哪种可以产生最佳性能。如 [13] 所示，两个实验中的性能均通过 ROC (AUROC) 和精确召回 (AUPR) 曲线下的面积进行评估。

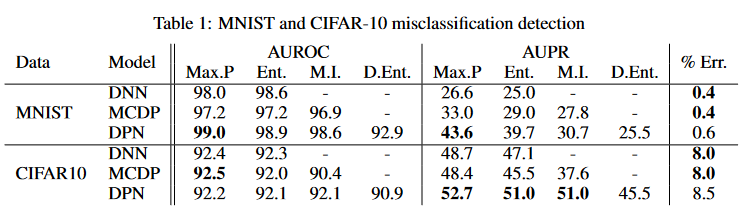
DPN的Err有所上升，但是微不足道；
有着很好的AUROC和AUPR，说明误分类检测能力增强，模型更加可信。
性能差异在 AUPR 上更为明显，它对不平衡的类很敏感。

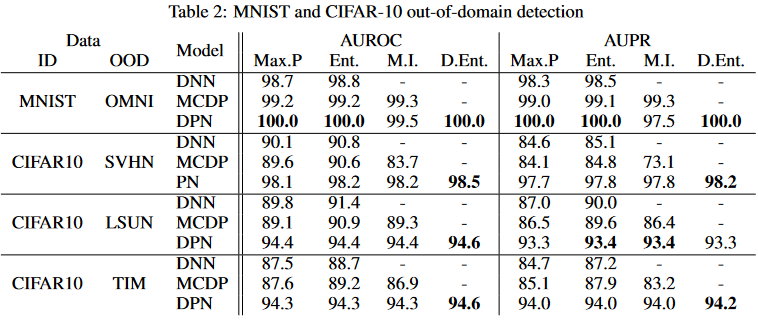
DPN consistently outperforms the baselines in OOD sample detection for both MNIST and CIFAR-10 datasets.始终优于基线！

1. DPN始终大幅优于基线；使用各种不确定性度量都是。
2. SVHN 和 LSUN和Cifar很大不同，高性能不足为奇，但是ImageNet上的表现亮眼

奇怪的是，MC dropout 并不总是比标准 DNN 产生更好的结果，这支持了贝叶斯分布很难在分布上实现所需行为的断言。

上面的实验1、2似乎表明微分熵和互信息相比于标准熵没有什么好处。

然而，这是因为 MNIST 和 CIFAR-10 是低数据不确定性数据集 ——所有类别都是差异明显的。
有趣的是，当类别不太明显时，狄利克雷先验的微分熵是否能够比熵更好地区分域内数据和分布外数据。

为此，在 MNIST 数据集上进行训练和评估期间，将标准差为 $\sigma =3$ 的零均值各向同性高斯噪声添加到 DNN 和 DPN 的输入中。表 3 显示，在存在强噪声的情况下，熵和 MI 无法成功区分ID和OOD样本，而使用微分熵的性能几乎没有下降。

因此可知，微分熵似乎不受数据不确定性影响，可以干净地衡量分布不确定性？
我理解对了吗？😢

6 Conclusion

这项工作描述了先前在不确定性来源的背景下预测不确定性估计的局限性，并建议将分布外（OOD）输入视为一个单独的不确定性来源，称为分布不确定性。

为此，这项工作提出了一个称为先验网络（PN）的新颖框架，它允许在一致的概率可解释框架内单独处理数据、分布和模型不确定性。

这些 PN 的一种特殊形式应用于分类，即狄利克雷先验网络 (DPN)。

1. 在 MNIST 和 CIFAR-10 数据集上的 OOD 检测任务中，DPN 比 MC Dropout 和标准 DNN 能产生更准确的分布不确定性估计。
2. DPN 在错误分类检测任务上也优于其他方法。

在他们评估的不确定性类型的背景下提出和分析了一系列不确定性度量。
值得注意的是，预测分布的最大概率在错误分类检测方面产生了最佳结果。
DPN 的微分熵最适合 OOD 检测，尤其是当类别不太明显时。这在合成实验和噪声损坏的 MNIST 任务中得到了说明。

可以在 DPN 测试时分析计算不确定性度量，从而相对于集成方法降低计算成本。
研究了用于图像分类的 PN 后，将它们应用于其他任务计算机视觉、NLP、机器翻译、语音识别和强化学习是很有趣的。最后，有必要探索用于回归任务的先验网络。

Appendix A Experimental Setup and Datasets

对于在 MNIST 数据上训练的 DPN，使用具有 50 维潜在空间的因子分析模型（Factor Analysis model）来合成分布外数据。在标准因子分析中，潜在向量具有各向同性标准正态分布。为了推动 FA 模型在域内区域的边界生成数据，增加了潜在分布的方差。

使用因子分析的目的是通过调整潜在空间（在这里是50维）的分布来生成新的数据点，这些数据点在结构上与MNIST数据相似，但在分布上有所不同。

• 在标准因子分析中，如果潜在向量的分布是标准正态分布，那么生成的数据将会紧密围绕着MNIST数据的中心。
• 通过增加潜在分布的方差，可以使得生成的数据点更加分散，有助于探索MNIST数据集在潜在空间中的边界区域。这意味着生成的数据可以更加多样化，从而更有可能包括OOD样本。

Appendix B Additional Experiments

Appendix C Derivations for Uncertainty Measures and KL divergence

本附录提供了推导，并展示了如何计算第 4 节中讨论的 DNN/DPN 和贝叶斯蒙特卡洛集成的不确定性度量。此外，它还描述了如何计算两个狄利克雷分布之间的 KL 散度

Entropy of Predictive Distribution for Bayesian MC

EnsembleDifferential Entropy of Dirichlet Prior Network

Mutual Information for Dirichlet Prior Network

KL Divergence between two Dirichlet Distributions

• 😢😢😢😢这几个推导没自己推呢，抽空推一下

[21] A. Malinin, A. Ragni, M.J.F. Gales, and K.M. Knill, “Incorporating Uncertainty into Deep Learning for Spoken Language Assessment,” in Proc. 55th Annual Meeting of the Association for Computational Linguistics (ACL), 2017.

[22] Kimin Lee, Honglak Lee, Kibok Lee, and Jinwoo Shin, “Training confidence-calibrated classifiers for detecting out-of-distribution samples,” International Conference on Learning Representations, 2018.

[32] Kevin P. Murphy, Machine Learning, The MIT Press, 2012.