【阅读笔记】神经网络中的LRP及其在非线性神经网络中的运用

最新推荐文章于 2023-12-27 17:57:45 发布

置顶 Hubery_Hao

最新推荐文章于 2023-12-27 17:57:45 发布

阅读量9.3k

点赞数 18

分类专栏：机器学习可解释性文章标签：机器学习神经网络

本文链接：https://blog.csdn.net/ChangHao888/article/details/109320053

版权

机器学习同时被 2 个专栏收录

2 篇文章 0 订阅

订阅专栏

可解释性

2 篇文章 0 订阅

订阅专栏

Layer-Wise Relevance Propagation for Neural Networks with Local Renormalization Layers主要介绍了一种将LRP扩展到非线性神经网络的方法。LRP是从模型输出开始，反向传播，直到模型输入开始为止，对由输入特征导致其预测结果的解释，文章中主要探究图片像素点与最终结果的相关性。

神经网络中的LRP(Layer-Wise Relevance Propagation)

$x_{j}=g\left ( \sum_{i=1}^{ } w_{ij}x_{i}+b \right )$

式中 $x_{j}$ 是神经元 $j$ 的输出， $g$ 是神经元 $j$ 的激活函数， $w_{ij}$ 是神经元 $i$ 到神经元 $j$ 的连接权重， $b$ 为连接偏差；

$f\left ( x \right )\approx \sum_{p}^{ } R_{p}^{\left ( 1 \right )}$

式中 $R_{p}^{\left ( 1 \right )}$ (pixel-wise relevance score) 用于衡量像素点对预测结果的影响， $R_{p}^{\left ( 1 \right )}> 0$ 表示某类在图片中存在的证据， $R_{p}^{\left ( 1 \right )}< 0$ 表示某类在图片中不存在的证据， $f\left ( x \right )$ 表示对图片 $x$ 的预测结果，预测结果可视为每个像素点对应 $R_{p}^{\left ( 1 \right )}$ 的总和。找出图片 $x$ 中所有像素点的 $R_{p}^{\left ( 1 \right )}$ 可将图片 $x$ 可视化为热图，如下：

（图片1）

假设已知第 $l+1$ 层神经元 $j$ 的相关性 $R_{j}^{\left ( l+1 \right )}$ ，可将该相关性 $R_{j}^{\left ( l+1 \right )}$ 分解到第 $l$ 层的所有神经元上，公式如下：

$R_{j}^{\left ( l+1 \right )}=\sum_{i\in \left ( l \right )}^{ }R_{i\leftarrow j}^{\left ( l,l+1 \right )}$

第 $l$ 层神经元 $i$ 的相关性 $R_{i}^{\left ( l \right )}$ 可理解为，第 $l+1$ 层中所有神经元的相关性分解后再进行求和，公式如下：

$R_{i}^{\left ( l \right )}=\sum_{j\in \left ( l+1 \right )}^{ }R_{i\leftarrow j}^{\left ( l,l+1 \right )}$

LRP传播机制示例如如下，有助于理解上述两个公式。

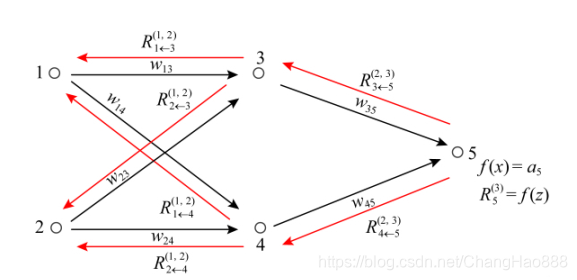
（图片2）LRP传播机制示例图

$R_{i\leftarrow j}^{\left ( l,l+1 \right )}$ 计算方式有两种： $\varepsilon -rule$ 与 $\beta -rule$

$\varepsilon -rule$ 如下：

$R_{i\leftarrow j}^{\left ( l,l+1 \right )}=\frac{z_{ij}}{z_{j}+\varepsilon \cdot sign\left ( z_{j} \right )}R_{j}^{\left ( l+1 \right )}$

式中 $z_{ij}=\left ( w_{ij}x_{j} \right )^{p}$ ， $z_{j}=\sum_{k,w_{ij}\neq 0}^{ }z_{kj}$ ，笔者认为文章中给出的 $z_{ij}$ 不是很好理解，稍作修改后如下：

$z_{ij}=a_{i}^{\left ( l \right )}w_{ij}^{\left ( l,l+1 \right )}$

$z_{ij}$ 为第 $l$ 层神经元 $i$ 对第 $l+1$ 层神经元 $j$ 的加权激活， $z_{j}$ 为第 $l$ 层所有神经元对第 $l+1$ 层神经元 $j$ 的加权激活。

$\beta -rule$ 如下：

$R_{i\leftarrow j}^{\left ( l,l+1 \right )}=\left ( \left ( 1+\beta \right )\frac{z_{ij}^{+}}{z_{j}^{+}}-\beta \frac{z_{ij}^{-}}{z_{j}^{-}} \right )R_{j}^{\left ( l+1 \right )}$

式中“+”与“- $_$ ”分别表示正值部分与负值部分，即上述公式将正负加权激活分开进行处理。

$R_{i\leftarrow j}^{\left ( l,l+1 \right )}$ 含义如下：

若第 $l$ 层某个神经元 $i$ 对第 $l+1$ 层神经元的一个神经元 $j$ 做出了主要贡献，那么第 $l$ 层神经元 $i$ 应该占第 $l+1$ 层神经元 $j$ 的相关性 $R_{j}^{\left ( l+1 \right )}$ 的较大份额，即神经元 $i$ 收集它对后一层所连接的神经元 $j$ 的贡献。

$R_{i\leftarrow j}^{\left ( l,l+1 \right )}$ 的两种计算方法 $\varepsilon -rule$ 与 $\beta -rule$ 实际上都是将第 $l+1$ 层神经元 $j$ 的相关性 $R_{j}^{\left ( l+1 \right )}$ 按照比例分配给第 $l$ 层神经元 $i$ 从而求得相关系数 $R_{i\leftarrow j}^{\left ( l,l+1 \right )}$ ，因此在LRP中，存在以下的结构：

$R_{i\leftarrow j}^{\left ( l,l+1 \right )}=v_{ij}R_{j}^{\left ( l+1 \right )}$ with $\sum_{i}^{ }v_{ij}=1$

式中 $v_{ij}=\frac{z_{ij}}{z_{j}+\varepsilon \cdot sign\left ( z_{j} \right )}$ 或 $v_{ij}=\left ( \left ( 1+\beta \right )\frac{z_{ij}^{+}}{z_{j}^{+}} -\beta \frac{z_{ij}^{-}}{z_{j}^{-}}\right )$ ，对于 $v_{ij}=\frac{z_{ij}}{z_{j}+\varepsilon \cdot sign\left ( z_{j} \right )}$ ，笔者认为应该是 $\sum_{i}^{ }v_{ij}\approx 1$ ，因为式中的 $\varepsilon$ 是一个较小的实数。

将LRP运用到非线性神经网络

先考虑一种情况：神经元 $j$ 的输出无法用等式 $x_{j}=g\left ( \sum_{i=1}^{ } w_{ij}x_{i}+b \right )$ 表示，设神经元 $j$ 的输出为 $x_{j}=g\left ( x_{h1},x_{h2},...,x_{hn} \right )$ ，式中 $x_{hi}, i=1,...n$ 表示神经元 $j$ 前一层神经元对神经元 $j$ 的输入，现将 $x_{j}$ 在参考点 $\left ( \tilde{x}_{h1},\tilde{x}_{h2},...,\tilde{x}_{hn} \right )$ 处进行一阶泰勒展开得如下式子：

$x_{j}\approx g\left ( \tilde{x}_{h1},\tilde{x}_{h2},...,\tilde{x}_{hn} \right )+\sum_{i\leftarrow j}^{ }\frac{\partial g}{\partial x_{hi}}\left ( \tilde{x}_{h1},\tilde{x}_{h2},...,\tilde{x}_{hn} \right )\left ( x_{hi}-\tilde{x}_{hi} \right )$

前一层神经元 $i$ 对后一层神经元 $j$ 的加权激活如下：

$\forall _{i\leftarrow j}:z_{ij}=\frac{1}{n}g\left ( \tilde{x}_{h1},\tilde{x}_{h2},...,\tilde{x}_{hn} \right )+\frac{\partial g}{\partial x_{hi}}\left ( \tilde{x}_{h1},\tilde{x}_{h2},...,\tilde{x}_{hn} \right )\left ( x_{hi}-\tilde{x}_{hi} \right )$

上式可理解为，将 $x_{j}$ 泰勒分解中的零阶项平均分配后，再加上前一层对应神经元 $i$ 输入的偏导值，即为前一层神经元 $i$ 对后一层神经元 $j$ 的加权激活。按照泰勒分解求得 $z_{ij}$ 后，可利用本文上述所介绍的 $\varepsilon -rule$ 或者 $\beta -rule$ 进行逐层相关性的求解，最终可计算出 $R_{p}^{\left ( 1 \right )}$ (pixel-wise relevance score)。

将LRP运用到Local Renormalization Layers

因Local Renormalization Layers在深度神经网络中表现出了良好的性能，所以在这里介绍将LRP运用到Local Renormalization Layers中，使其具有可解释性。

将神经网络中某一层设置为Local Renormalization Layers，该层中神经元定义如下：

$y_{k}\left ( x_{1},x_{2},...,x_{n} \right )=\frac{x_{k}}{\left ( 1+b\sum_{i=1}^{n}x_{i}^{2} \right )^{c}}$

显然，Local Renormalization Layers为非线性，可将LRP运用到非线性神经网络的方法应用到此处。

将 $y_{k}\left ( x_{1},x_{2},...,x_{n} \right )$ 在参考点 $\left ( \tilde{x}_{h1},\tilde{x}_{h2},...,\tilde{x}_{hn} \right )$ 处进行泰勒展开可得如下式子：

$y_{k}\approx y_{k}\left ( \tilde{x}_{h1},\tilde{x}_{h2},...,\tilde{x}_{hn} \right )+\sum_{i}^{ }\frac{\partial y_{k}}{\partial x_{hi}}\left ( \tilde{x}_{h1},\tilde{x}_{h2},...,\tilde{x}_{hn} \right )\left ( x_{hi}-\tilde{x}_{hi} \right )$

对 $y_{k}$ 求偏导，如下：

$\frac{\partial y_{k}}{\partial x_{j}}=-\frac{2bcx_{j}x_{k}}{\left ( 1+b \sum_{i=1}^{n}x_{i}^{2}\right )^{c+1}}$ ，此处 $j\neq k$

$\frac{\partial y_{k}}{\partial x_{j}}=\frac{1}{\left ( 1+b\sum_{i=1}^{n}x_{i}^{2} \right )^{c}}-\frac{2bcx_{j}x_{k}}{\left ( 1+b \sum_{i=1}^{n}x_{i}^{2}\right )^{c+1}}$ ，此处 $j=k$

将上面两个式中，稍作整理可得，

$\frac{\partial y_{k}}{\partial x_{j}}=\frac{\delta_{jk}}{\left ( 1+b\sum_{i=1}^{n}x_{i}^{2} \right )^{c}}-\frac{2bcx_{j}x_{k}}{\left ( 1+b \sum_{i=1}^{n}x_{i}^{2}\right )^{c+1}}$

对于输出为 $y_{k}$ 的神经元来说，其输入应该是 $z_{1}=\left ( x_{1},x_{2},...,x_{n} \right )$ ，若只有输出为 $x_{k}$ 的神经元触发输出为 $y_{k}$ 的神经元时，其输入应该是 $z_{2}=\left ( 0,0,...,x_{k},...,0 \right )$ ，即对于输出为 $y_{k}$ 的神经元，我们选择在只有输出为 $x_{k}$ 的神经元触发输出为 $y_{k}$ 的神经元时候展开，即在点 $z_{2}$ 展开，如下：

$y_{k}\left ( z_{1} \right )\approx y_{k}\left ( z_{2} \right )+0=\frac{x_{k}}{\left ( 1+bx_{k}^{2} \right )^{c}}$

上式则意味着 $y_{k}$ 的泰勒一阶展开式中一阶项对于 $y_{k}$ 的近似没有贡献值，这是我们不希望看到的，故稍作修改，如下：

$y_{k}\left ( z_{2} \right )\approx y_{k}\left ( z_{1} \right )+\bigtriangledown y_{k}\left ( z_{1} \right )\left ( z_{2}-z_{1} \right )$

$\Rightarrow y_{k}\left ( z_{1} \right )\approx y_{k}\left ( z_{2} \right )+\bigtriangledown y_{k}\left ( z_{1} \right )\left ( z_{1}-z_{2} \right )$

$\Rightarrow y_{k}\left ( z_{1} \right )\approx \frac{x_{k}}{\left ( 1+bx_{k}^{2} \right )^{c}}-2bc\sum_{j,j\neq k}^{ }\frac{x_{k}x_{j}^{2}}{\left ( 1+b\sum_{i=1}^{n}x_{i}^{2} \right )^{c+1}}$

然后根据求得的 $y_{k}\left ( z_{1} \right )$ 可通过如下式子计算前一层神经元 $i$ 对后一层神经元 $j$ 的加权激活 $z_{ij}$ ，

最后可利用本文在最前面所介绍的 $\varepsilon -rule$ 或者 $\beta -rule$ 进行逐层相关性的求解，最终可计算出 $R_{p}^{\left ( 1 \right )}$ (pixel-wise relevance score)。

笔者水平有限，难免存在理解不当之处，欢迎批评指正，联系邮箱：changhao1997@foxmail.com

参考文献

Layer-Wise Relevance Propagation for Neural Networks with Local Renormalization Layers
赵新杰. 深度神经网络的可视化理解方法研究[D].哈尔滨工程大学,2018.
陈珂锐,孟小峰.机器学习的可解释性[J].计算机研究与发展,2020,57(09):1971-1986.