总体和样本均值的符号:
- n = 样本容量
- u = 总体均值
- x = 样本均值
- σ = 总体标准差
- s = 样本标准差
样本均值分布的特征:
对于任何样本均值的分布:
- 样本容量越大,样本均值的分布越接近正态分布
- 总体中所有样本均值的平均值与总体均值相等
- 总体中所有样本均值的标准差的表达式为 :
总体成数和样本成数符号:
- n = 样本容量
- p = 总体成数
 = 样本成数
= 样本成数
样本成数的分布:
样本成数的抽样分布是指给定容量时,源自所有可能样本的成数( )的分布
)的分布
注意:
样本容量越大,样本成数的分布越接近正态分布;
样本成数分布的平均值与总体成数相等
样本成数分布的标准差的表达式为 : 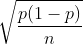 。
。
用样本均值估计总体均值:
假设计算出样本均值x,它来自于总体的一个样本。接下来估计总体均值:
- 因为只有一个样本均值,我们把它当作总体均值最佳(唯一)的估计量;
- 基于样本容量和样本标准差(s),计算误差的范围,并用它建立一个置信区间,然后可以陈述估计总体均值的质量有多高。
样本均值的误差幅度 = 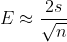
总体均值的置信区间:
95%的置信区间范围:( - 误差幅度) 到 (
- 误差幅度) 到 ( + 误差幅度)
+ 误差幅度)
最大误差幅度E的总体均值,样本容量至少为: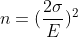
σ = 总体标准差
95%的置信区间的误差幅度是: E ≈ 2 根号 p^(1-p^)/n = 样本成数
= 样本成数
样本成数的置信区间:
95%的置信区间范围:( - 误差幅度) 到 (
- 误差幅度) 到 ( + 误差幅度)
+ 误差幅度)
选择正确的样本容量:
为了在95%的置信水平和特定的误差幅度E条件下估计总体成数,样本容量至少应该为:
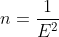

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








