- 基本概念
- 决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
- 三种结点:
- 根结点:没有入边,但有零条或者多条出边
- 内部结点:恰有一条入边和两条或多条出边
- 叶结点:恰有一条入边,但没有出边
- 种类:
- 分类树:对离散变量做决策树
- 回归树:对连续变量做决策树
- 相关数学知识
- 信息熵(entropy):
信息熵就是平均而言发生一个事件我们得到的信息量大小。所以数学上,信息熵其实是信息量的期望。(参见知乎:https://www.zhihu.com/question/22178202)
理解:
熵:表示随机变量的不确定性。
条件熵:在一个条件下,随机变量的不确定性。
信息增益:熵- 条件熵,在一个条件下,信息不确定性减少的程度。
通俗地讲,X(明天下雨)是一个随机变量,X的熵可以算出来,Y(明天阴天)也是随机变量,在阴天情况下下雨的信息熵我们如果也知道的话(此处需要知道其联合概率分布或是通过数据估计)即是条件熵。两者相减就是信息增益!原来明天下雨例如信息熵是2,条件熵是0.01(因为如果是阴天就下雨的概率很大,信息就少了),这样相减后为1.99,在获得阴天这个信息后,下雨信息不确定性减少了1.99,是很多的,所以信息增益大。也就是说,阴天这个信息对下雨来说是很重要的!
所以在特征选择的时候常常用信息增益,如果IG(信息增益大)的话那么这个特征对于分类来说很关键,决策树就是这样来找特征的。
(参见知乎:








 本文介绍了决策树的基本概念,包括分类树和回归树,并深入讲解了信息熵、条件熵和信息增益等核心概念,用于特征选择。此外,还探讨了基尼指数在决策树中的应用,以及ID3、C4.5和CART算法的差异。最后,通过sklearn库展示了如何在Python中实现决策树,并提供了参数调优的建议。
本文介绍了决策树的基本概念,包括分类树和回归树,并深入讲解了信息熵、条件熵和信息增益等核心概念,用于特征选择。此外,还探讨了基尼指数在决策树中的应用,以及ID3、C4.5和CART算法的差异。最后,通过sklearn库展示了如何在Python中实现决策树,并提供了参数调优的建议。
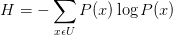
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 927
927

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








