一.原理
1.常微分方程的离散化
下面主要讨论一阶常微分方程的初值问题，其一般形式为
由常微分方程理论，初值问题（1）的解必定存在唯一
所谓数值解法，就是球（1）的解y(x)在若干点
a = x0 < x1 < x2<...<xn=b
处的近似值yn的方法。h=xn+1-xn称为补偿，取步长h为常量
1.1 用差商近似倒数
1.2 数值积分方法
1.3 Taylor多项式近似
以上三种方法都是将微分方程离散化的常用方法，每一类方法又可导出不同形式的计算公式。其中的 Taylor 展开法，不仅可以得到求数值解的公式，而且容易估计截断误差。
2.Euler方法
2.1 Euler方法
2.2 Euler方法的误差估计
3.改进的Euler方法
3.1 梯形公式
3.2 改进Euler方法
4.Runge-Kutta方法
5.线性多步法
以上所介绍的各种数值解法都是单步法，这是因为它们在计算yn+1时，都只用到前一步的值 yn，单步法的一般形式是
6.一阶微分方程组的数值解法
6.1 一阶微分方程组的初值问题
6.2 高阶微分方程组的数值解法
二.初值问题的Matlab解法和符号解
2.1 Matlab数值解
2.1.1非刚性常微分方程的解法
Matlab 的工具箱提供了几个解非刚性常微分方程的功能函数，如 ode45，ode23， ode113，其中 ode45 采用四五阶 RK 方法，是解非刚性常微分方程的首选方法，ode23 采用二三阶 RK 方法，ode113 采用的是多步法，效率一般比 ode45 高。 Matlab 的工具箱中没有 Euler 方法的功能函数。
首先编写改进的Euler方法函数eulerpro.m
function [x, y] = eulerpro(fun, x0, xfinal, y0, n);
if nargin < 5, n=50;end
h = (xfinal - x0) / n;
x(1) = x0;
y(1) = y0;
for i = 1:n
x(i + 1) = x(i) + h;
y1 = y(i) + h * feval(fun,x(i), y(i));
y2 = y(i) + h * feval(fun, x(i + 1), y1);
y(i + 1) = (y1 + y2) / 2;
end1.nargin：nargin 针对当前正在执行的函数，返回函数调用中给定函数输入参数的数目。该语法仅可在函数体内使用；nargin(fun) 返回 fun 函数定义中出现的输入参数的数目。如果该函数定义中包含 varargin，那么 nargin 返回输入数目的负数。
参考：Matlab nargin_勉为其难免免的博客-CSDN博客_matlab nargin
2.n:表示x区间分割次数。如果没有输入n的值，默认取50
3.feval函数：feval()函数执行指定的函数。也就是说，将想要执行的函数以及相应的参数一起作为feval()的参数，feval()的输出等于想要执行的函数的输出。参考：MATLAB中feval函数的用法_「已注销」的博客-CSDN博客_matlab feval函数
编写函数文件doty.m如下：
function f = doty(x, y)
f = -2 * y + 2 * x^2 + 2 * x;
在Matlab命令窗口输入：
[x, y]=eulerpro('doty', 0, 0.5, 1, 10)即可的数值解：
在命令窗口输入：
[x, y] = ode45('doty', [0, 0.5], 1)即可求数值解
2.1.2 刚性常微分方程的解法
Matlab的工具箱提供了几个解刚性常微分方程的功能函数，如ode15s，ode23s， ode23t，ode23tb，这些函数的使用同上述非刚性微分方程的功能函数。
2.1.3 高阶微分方程的解法
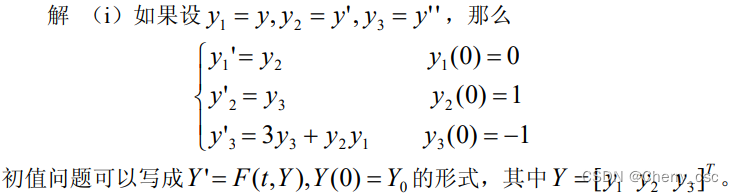
function dy = F(t, y)
dy = [y(2); y(3); 3 * y(3) + y(2) * y(1)];注意：尽管不一定用到参数t和y，M文件必须接受此两参数。这里dy必须是列向量
（Ⅲ）用matlab解决此问题的函数形式为：
[T,Y]=solver('F',tspan,y0)
这里 solver 为 ode45、ode23、ode113，输入参数 F 是用 M 文件定义的常微分方程组， tspan=[t0 tfinal]是求解区间，y0 是初值列向量。
不同求解器对比如下表：
| 求解器 | 问题类型 | 精度 | 何时使用 |
|---|---|---|---|
| ode45 | 非刚性 | 中 | 大多数情况下，您应当首先尝试求解器 |
| ode23 | 低 | 对于容差较宽松的问题或在刚度适中的情况下， | |
| ode113 | 低到高 | 对于具有严格误差容限的问题或在 ODE 函数需要大量计算开销的情况下， | |
| ode78 | 高 | 对于具有高准确度要求的平滑解的问题， | |
| ode89 | 高 | 对于非常平滑的问题，当在较长的时间区间内进行积分时，或当容差特别严格时， | |
| ode15s | 刚性 | 低到中 | 若 |
| ode23s | 低 | 对于误差容限较宽松的问题，
如果存在质量矩阵，则它必须为常量矩阵。 | |
| ode23t | 低 | 对于仅仅是刚度适中的问题，并且您需要没有数值阻尼的解，请使用
| |
| ode23tb | 低 | 与 | |
| ode15i | 完全隐式 | 低 | 对于完全隐式问题 f(t,y,y’) = 0 和微分指数为 1 的微分代数方程 (DAE)，请使用 |
参考：选择 ODE 求解器- MATLAB & Simulink- MathWorks 中国
在命令窗口输入
[T, Y] = ode45('F', [0 1], [0; 1; -1])就得到上述常微分方程的数值解：
T =
0
0.0001
0.0001
0.0002
0.0002
0.0005
0.0007
0.0010
0.0012
0.0025
0.0037
0.0050
0.0062
0.0125
0.0188
0.0251
0.0313
0.0563
0.0813
0.1063
0.1313
0.1563
0.1813
0.2063
0.2313
0.2563
0.2813
0.3063
0.3313
0.3563
0.3813
0.4063
0.4313
0.4563
0.4813
0.5063
0.5313
0.5563
0.5813
0.6063
0.6313
0.6563
0.6813
0.7063
0.7313
0.7563
0.7813
0.8063
0.8313
0.8563
0.8813
0.9063
0.9313
0.9485
0.9657
0.9828
1.0000
Y =
0 1.0000 -1.0000
0.0001 0.9999 -1.0002
0.0001 0.9999 -1.0003
0.0002 0.9998 -1.0005
0.0002 0.9998 -1.0006
0.0005 0.9995 -1.0014
0.0007 0.9993 -1.0021
0.0010 0.9990 -1.0029
0.0012 0.9988 -1.0036
0.0025 0.9975 -1.0074
0.0037 0.9963 -1.0112
0.0050 0.9950 -1.0150
0.0062 0.9937 -1.0188
0.0124 0.9873 -1.0382
0.0186 0.9807 -1.0578
0.0247 0.9740 -1.0778
0.0308 0.9671 -1.0981
0.0547 0.9386 -1.1826
0.0778 0.9080 -1.2731
0.1000 0.8749 -1.3702
0.1215 0.8394 -1.4745
0.1420 0.8011 -1.5865
0.1615 0.7600 -1.7070
0.1800 0.7157 -1.8367
0.1973 0.6681 -1.9763
0.2133 0.6168 -2.1268
0.2281 0.5616 -2.2891
0.2414 0.5022 -2.4641
0.2532 0.4383 -2.6530
0.2633 0.3695 -2.8569
0.2716 0.2953 -3.0771
0.2780 0.2155 -3.3150
0.2823 0.1294 -3.5719
0.2844 0.0367 -3.8495
0.2841 -0.0632 -4.1494
0.2812 -0.1710 -4.4734
0.2755 -0.2871 -4.8234
0.2667 -0.4124 -5.2015
0.2548 -0.5475 -5.6099
0.2393 -0.6931 -6.0508
0.2200 -0.8503 -6.5266
0.1967 -1.0198 -7.0400
0.1689 -1.2026 -7.5936
0.1364 -1.3998 -8.1902
0.0988 -1.6125 -8.8326
0.0556 -1.8419 -9.5240
0.0065 -2.0891 -10.2674
-0.0490 -2.3557 -11.0659
-0.1114 -2.6429 -11.9226
-0.1813 -2.9523 -12.8406
-0.2592 -3.2855 -13.8229
-0.3458 -3.6440 -14.8723
-0.4417 -4.0297 -15.9915
-0.5132 -4.3110 -16.8015
-0.5897 -4.6066 -17.6459
-0.6714 -4.9170 -18.5255
-0.7586 -5.2427 -19.4404这里Y和时刻T是一一对应的。Y(:,1)是初值问题的 解，Y(:,2)是解的导数，Y(:,3)是解的二阶导数。
2.2 常微分方程的解析解
在 Matlab 中，符号运算工具箱提供了功能强大的求解常微分方程的符号运算命令 dsolve。常微分方程在 Matlab 中按如下规定重新表达：
符号 D 表示对变量的求导。Dy 表示对变量 y 求一阶导数，当需要求变量的 n 阶导 数时，用 Dn 表示，D4y 表示对变量 y 求 4 阶导数。
2.2.1 求解常微分方程的通解
无初边值条件的常微分方程的解就是该方程的通解。其使用格式为：
dsolve('diff_equation')
dsolve(' diff_equation'，'var')
式中 diff_equation 为待解的常微分方程，第 1 种格式将以变量 t 为自变量进行求解， 第 2 种格式则需定义自变量 var
（##需要Symbolic Math Toolbox##）
syms x y
diff_equ = 'x^2 + y + (x - 2 * y) * Dy = 0';
dsolve(diff_equ, 'x') 结果：
2.2.2 求解常微分方程的初边值问题
求解带有初边值条件的常微分方程的使用格式为： dsolve('diff_equation'，'condition1，condition2，…'，'var')
其中 condition1，condition2，… 即为微分方程的初边值条件。
y = dsolve('D3y - D2y=x','y(1)=8,Dy(1)=7, D2y(2)=4', 'x') 结果：
2.2.3 求解常微分方程组
求解常微分方程组的命令格式为：
dsolve('diff_equ1，diff_equ2，…'，'var')
dsolve('diff_equ1，diff_equ2，…'，'condition1，condition2，…'，'var')
第 1 种格式用于求解方程组的通解，第 2 种格式可以加上初边值条件，用于具体求解。
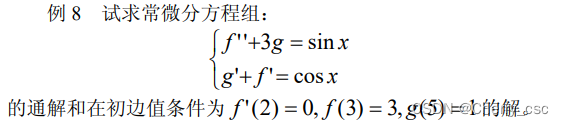
clc,clear
equ1='D2f+3*g=sin(x)';
equ2='Dg+Df=cos(x)';
[general_f,general_g]=dsolve(equ1,equ2,'x')
[f,g]=dsolve(equ1,equ2,'Df(2)=0,f(3)=3,g(5)=1','x') 其中general_f, general+g是求通解
2.2.4 求解线性常微分方程组
（1） 一阶齐次线性微分方程组
syms t
a=[2,1,3;0,2,-1;0,0,2];
x0=[1;2;1];
x=expm(a*t)*x0expm是矩阵形式的指数函数的泰勒展开，即将其中的x改为矩阵A。X'=AX的解为X=c*exp(AX)。如何定义矩阵幂的指数函数，只需将其泰勒展开即可，因此x的解析解可以通过expm函数求解。
expm函数参考：matlab expm_硫酸铝的博客-CSDN博客_matlab expm
（2） 非齐次线性方程组
clc,clear
syms t s
a=[1,0,0;2,1,-2;3,2,1];ft=[0;0;exp(t)*cos(2*t)];
x0=[0;1;1];
x=expm(a*t)*x0+int(expm(a*(t-s))*subs(ft,s),s,0,t);
x=simplify(x) int：求符号函数的定积分，其调用格式如下：
int(F,x,a,b)。
a表示定积分的下限；b表示定积分的上限；subs：符号计算函数，表示将符号表达式中的某些符号变量替换为指定的新的变量，subs(s,old,new)表示将符号表达式s中的符号变量old替换为新的值new
simplify:simplify(s), 对表达式进行化简
subs参考：【MATLAB】matlab中的subs()函数和solve()函数用法_啦啦不要熬夜啊的博客-CSDN博客_matlab subs函数
2.3 边值问题的Matlab解法
上述微分方程组可以由如下函数表示：
function yprime=drop(x,y);
yprime=[y(2);(y(1)-1)*(1+y(2)^2)^(3/2)];边界条件通过残差函数指定，边界条件通过如下函数表示：
function res=dropbc(ya,yb);
res=[ya(1);yb(1)];
function yinit=dropinit(x);
yinit=[sqrt(1-x.^2);-x./(0.1+sqrt(1-x.^2))];利用如下的程序就可以求微分方程的边值问题并画出图：
solinit=bvpinit(linspace(-1,1,20),@dropinit);
sol=bvp4c(@drop,@dropbc,solinit);
fill(sol.x,sol.y(1,:),[0.7,0.7,0.7])
axis([-1,1,0,1])
xlabel('x','FontSize',12)
ylabel('h','Rotation',0,'FontSize',12)结果：
这里调用函数bvpinit，计算区间[−1,1]上等间距的20个点的数据，然后调用函数 bvp4c，得到数值解的结构sol，填充命令fill填充 1 x − y 平面上的解曲线。
bvp4c的调用格式如下：
sol=bvp4c(@odefun,@bcfun,solinit,options,p1,p2,…);
函数odefun的格式为：
yprime=odefun(x,y,p1,p2, …);
函数bcfun的格式为：
res=bcfun(ya,yb, p1,p2, …);
初始猜测结构solinit有两个域：solinit.x提供初始猜测的 x 值，排列顺序从 左到右排列，其中solinit.x(1)和solinit.x(end)分别为 a 和b 。对应地， solinit.y(:,i)给出点solinit.x(i)处初始猜测解。 输出参数sol是包含数值解的一个结构，其中sol.x给出了计算数值解的 x 点， sol.x(i)处的数值解由sol.y(:,i)给出，类似地，sol.x(i)处数值解的一阶导数 值由sol.yp(:,i)给出。
参考：求解边界值问题- MATLAB & Simulink- MathWorks 中国
用matlab的bvpc求解器解决最优控制问题（即两点边值问题）_最爱大盘鸡的博客-CSDN博客_matlab求解最优控制问题
2424
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
