在我图与网络模型及方法(一)的文章中介绍了图论相关模型与方法的原理,这篇文章将详细介绍一些经典的应用问题。
python中有个专门处理图、网络相关问题的库:networkx,以下部分应用代码实现部分给出直接调库的代码实现方法。
一.匹配问题





代码示例:
import numpy as np
import networkx as nx
# 匹配问题 二分图
worker_n = 5 # 工人数目
work_n = 5 # 工作数目
a = np.array([[3, 5, 5, 4, 1], [2, 2, 0, 2, 2], [2, 4, 4, 1, 0],
[0, 2, 2, 1, 0], [1, 2, 1, 3, 3]])
b = np.zeros((10, 10))
b[0:worker_n, work_n:] = a
G = nx.Graph(b)
s0 = nx.max_weight_matching(G) # 返回值为(人员、工作的集合)
s = [sorted(w) for w in s0]
L1 = np.array([x[0] for x in s]) # 人员编号
L2 = np.array([x[1] for x in s]) # 工作编号
c = []
for i in range(len(L1)):
c.append(a[L1[i]][L2[i] - worker_n])
d = sum(c) # 计算总的效益
print("工作分配对应关系为:")
print("人员编号:", L1 + 1)
print("工作编号:", L2 - worker_n + 1)
print("总效益:", d)
print('-------------------------------------------------')二.Euler图和Hamilton图
2.1 基本概念
定义
经过G的每条边的迹叫做G 的 Euler 迹;闭的 Euler 迹叫做 Euler回路或E回路;含 Euler回路的图叫做Euler图。直观地讲,Euler图就是从一顶点出发每边恰通过一次能回到出发点的那种图,即不重复地行遍所有的边再回到出发点。
Euler图最初是为了解决戈尼斯堡七桥问题
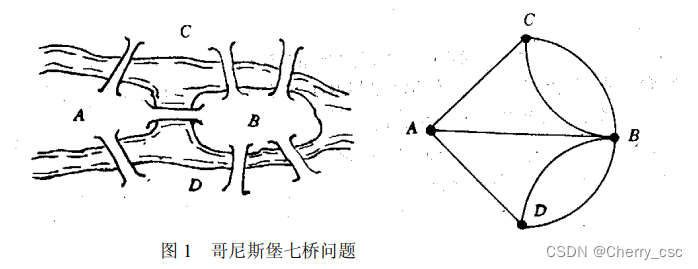

定义
包含G 的每个顶点的轨叫做 Hamilton(哈密顿)轨;闭的 Hamilton 轨叫做Hamilton 圈或 H 圈;含 Hamilton 圈的图叫做 Hamilton 图。
直观地讲,Hamilton 图就是从一顶点出发每顶点恰通过一次能回到出发点的那种图,即不重复地行遍所有的顶点再回到出发点
2.2 Euler回路的Fleury算法

python实现代码:Python实现Fleury算法_Paul_barnabas的博客-CSDN博客_fleury算法python
2.3 应用
2.3.1 邮递员问题
中国邮递员问题
一位邮递员从邮局选好邮件去投递,然后返回邮局,当然他必须经过他负责投递的每条街道至少一次,为他设计一条投递路线,使得他行程最短。
上述中国邮递员问题的数学模型是:在一个赋权连通图上求一个含所有边的回路,且使此回路的权最小。
显然,若此连通赋权图是 Euler 图,则可用 Fleury 算法求 Euler 回路,此回路即为所求。
对于非 Euler 图,1973 年,Edmonds 和 Johnson 给出下面的解法

多邮递员问题(kpp)
邮局有 k(k ≥ 2) 位投递员,同时投递信件,全城街道都要投递,完成任务返回邮 局,如何分配投递路线,使得完成投递任务的时间最早?


参考:中国邮递员问题的深入剖析与算法实现(附例题及MATLAB、LINGO代码)_第二号的博客-CSDN博客_中国邮递员问题例题
2.3.2 旅行商问题TSP
旅行商问题TSP
一名推销员准备前往若干城市推销产品,然后回到他的出发地。如何为他设计一条最短的旅行路线(从驻地出发,经过每个城市恰好一次,最后返回驻地)?这个问题称为旅行商问题。用图论的术语说,就是在一个赋权完全图中,找出一个有最小权的 Hamilton 圈。称这种圈为最优圈。
与最短路问题及连线问题相反,目前还没有求解旅行 商问题的有效算法。所以希望有一个方法以获得相当好(但不一定最优)的解。

function main
clc,clear
global a
a=zeros(6);
a(1,2)=56;a(1,3)=35;a(1,4)=21;a(1,5)=51;a(1,6)=60;
a(2,3)=21;a(2,4)=57;a(2,5)=78;a(2,6)=70;
a(3,4)=36;a(3,5)=68;a(3,6)=68; a(4,5)=51;a(4,6)=61;
a(5,6)=13; a=a+a'; L=size(a,1);
c1=[5 1:4 6];
[circle,long]=modifycircle(c1,L);
c2=[5 6 1:4];%改变初始圈,该算法的最后一个顶点不动
[circle2,long2]=modifycircle(c2,L);
if long2<long
long=long2;
circle=circle2;
end
circle,long
%*******************************************
%修改圈的子函数
%*******************************************
function [circle,long]=modifycircle(c1,L);
global a
flag=1;
while flag>0
flag=0;
for m=1:L-3
for n=m+2:L-1
if a(c1(m),c1(n))+a(c1(m+1),c1(n+1))<... a(c1(m),c1(m+1))+a(c1(n),c1(n+1))
flag=1;
c1(m+1:n)=c1(n:-1:m+1);
end
end
end
end
long=a(c1(1),c1(L));
for i=1:L-1
long=long+a(c1(i),c1(i+1));
end
circle=c1;其他求解方式有模拟退火、遗传算法等现代智能算法,如
import random
import math
import numpy as np
import matplotlib.pyplot as plt
# 随机初始化城市坐标
number_of_citys = 100
citys = []
for i in range(number_of_citys):
citys.append([random.randint(1, 100), random.randint(1, 100)])
citys = np.array(citys)
# 由城市的坐标计算距离矩阵
distance = np.zeros((number_of_citys, number_of_citys))
for i in range(number_of_citys):
for j in range(number_of_citys):
distance[i][j] = math.sqrt((citys[i][0] - citys[j][0])**2 +
(citys[i][1] - citys[j][1])**2)
# 初始化参数
iter1 = 2000 # 外循环迭代次数
T0 = 100000 # 初始温度
Tf = 1 # 截止温度
T_now = T0 # 当前温度
alpha = 0.95 # 温度更新因子
iter2 = 10 # 内循环迭代次数
fbest = 0 # 最佳距离
# 初始化初解
x = []
for i in range(number_of_citys):
x.append(i)
np.random.shuffle(x)
x = np.array(x)
fbest = float('inf')
xbest = x.copy()
f_now = fbest
x_now = xbest.copy()
for m in range(iter1):
for k in range(iter2):
# 生成新解
x1 = [0 for q in range(number_of_citys)]
n1 = random.randint(0, number_of_citys - 1)
n2 = random.randint(0, number_of_citys - 1) # 对路径进行“微扰”
n = [n1, n2]
n.sort()
n1, n2 = n
# n1 == 0 单独写
if n1 > 0:
x1[0:n1] = x_now[0:n1]
x1[n1:n2 + 1] = x_now[n2:n1 - 1:-1]
x1[n2 + 1:number_of_citys] = x_now[n2 + 1:number_of_citys]
else:
x1[0:n1] = x_now[0:n1]
x1[n1:n2 + 1] = x_now[n2::-1]
x1[n2 + 1:number_of_citys] = x_now[n2 + 1:number_of_citys]
s = 0
for j in range(len(x1) - 1):
s = s + distance[x1[j]][x1[j + 1]]
s += distance[x1[-1]][x1[0]]
# 判断是否有更新解
if s <= f_now:
f_now = s
x_now = x1.copy()
else:
if random.random() < math.exp((f_now - s) / T_now):
f_now = s
x_now = x1.copy()
if s < fbest: # 历史最优解
fbest = s
xbest = x1.copy()
T_now = T_now * alpha
print("最佳路线:", xbest)
print("最佳距离:", fbest)
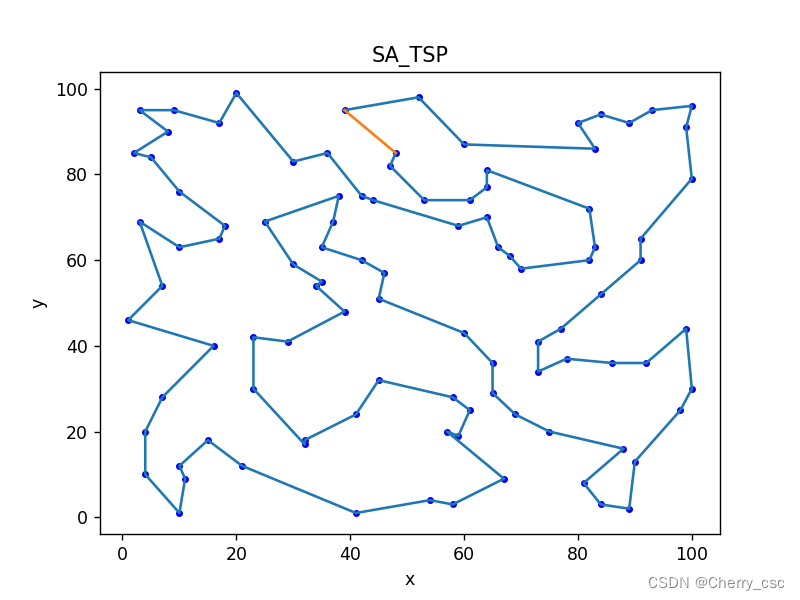
plt.title('SA_TSP')
plt.xlabel('x')
plt.ylabel('y')
plt.plot(citys[..., 0], citys[..., 1], 'ob', ms=3)
citys_x = []
citys_y = []
for i in xbest:
citys_x.append(citys[i][0])
citys_y.append(citys[i][1])
plt.plot(citys_x, citys_y)
plt.plot([citys[xbest[-1]][0], citys[xbest[0]][0]],
[citys[xbest[-1]][1], citys[xbest[0]][1]],
ms=2)
plt.show()结果:
三.最大流问题
3.1 最大流问题的数学描述
3.1.1 网络中的流
定义
在以V 为节点集, A 为弧集的有向图G = (V, A) 上定义如下的权函数:
(i) L : A → R 为孤上的权函数,弧 (i, j)∈ A 对应的权 L(i, j) 记为lij ,称为孤 (i, j) 的容量下界(lower bound);
(ii)U : A → R 为弧上的权函数,弧(i, j)∈ A对应的权U(i, j) 记为uij ,称为孤 (i, j) 的容量上界,或直接称为容量(capacity);
(iii) D :V → R 为顶点上的权函数,节点i ∈V 对应的权 D(i) 记为 di ,称为顶点i 的供需量(supply/demand);
此时所构成的网络称为流网络,可以记为
N = (V, A,L,U,D)

定义
3.1.2 最大流问题

定义
如果一个矩阵 A 的任何子方阵的行列式的值都等于0,1或 −1,则称 A 是全幺模的(totally unimodular TU,又译为全单位模的),或称A是全幺模矩阵。
定理
(整流定理) 最大流问题所对应的约束矩阵是全幺模矩阵。若所有弧容量均为正整数,则问题的最优解为整数解
最大流问题是一个特殊的线性规划问题。我们将会看到利用图的特点,解决这个问 题的方法较之线性规划的一般方法要方便、直观得多。
3.1.3 单源和单汇运输网络

3.2 最大流和最小割关系


3.3 最大流的一种算法——标号法




clc,clear
u(1,2)=1;u(1,3)=1;u(1,4)=2;u(2,3)=1;u(2,5)=2;
u(3,5)=1;u(4,3)=3;u(4,5)=3;
f(1,2)=1;f(1,3)=0;f(1,4)=1;f(2,3)=0;f(2,5)=1;
f(3,5)=1;f(4,3)=1;f(4,5)=0;
n=length(u);list=[];maxf(n)=1;
while maxf(n)>0
maxf=zeros(1,n);pred=zeros(1,n);
list=1;record=list;maxf(1)=inf;
%list是未检查邻接点的标号点,record是已标号点
while (~isempty(list))&(maxf(n)==0)
flag=list(1);list(1)=[];
label1= find(u(flag,:)-f(flag,:));
label1=setdiff(label1,record);
list=union(list,label1);
pred(label1)=flag;
maxf(label1)=min(maxf(flag),u(flag,label1)... -f(flag,label1));
record=union(record,label1);
label2=find(f(:,flag));
label2=label2';
label2=setdiff(label2,record);
list=union(list,label2);
pred(label2)=-flag;
record=union(record,label2);
end
if maxf(n)>0
v2=n; v1=pred(v2);
while v2~=1
if v1>0
f(v1,v2)=f(v1,v2)+maxf(n);
else
v1=abs(v1);
f(v2,v1)=f(v2,v1)-maxf(n);
end
v2=v1; v1=pred(v2);
end
end
end
f
或者通过使用networkx中maximum_flow函数直接求解最大流问题
import networkx as nx
# 最大流问题
L = [(1, 2, 5), (1, 3, 3), (2, 4, 2), (3, 2, 1), (3, 5, 4), (4, 3, 1),
(4, 5, 3), (5, 6, 5)]
G = nx.DiGraph()
for k in range(len(L)):
G.add_edge(L[k][0] - 1, L[k][1] - 1, capacity=L[k][2])
value, flow_dict = nx.maximum_flow(G, 0, 5)
print("最大流的流量为:", value)
print("最大流为:", flow_dict) # 最大流情形下, 每条边实际流量四.最小费用流及其求法
4.1 最小费用流
上面我们介绍了一个网络上最短路以及最大流的算法,但是还没有考虑到网络上流的费用问题,在许多实际问题中,费用的因素很重要。例如,在运输问题中,人们总是希望在完成运输任务的同时,寻求一个使总的运输费用最小的运输方案。这就是下面要 介绍的最小费用流问题。

4.2 求最小费用流的一种方法——迭代法



matlab代码如下:
function mainexample19
clear;clc;
global M num
c=zeros(6);u=zeros(6);
c(1,2)=2;c(1,4)=8;c(2,3)=2;c(2,4)=5;
c(3,4)=1;c(3,6)=6;c(4,5)=3;c(5,3)=4;c(5,6)=7;
u(1,2)=8;u(1,4)=7;u(2,3)=9;u(2,4)=5;
u(3,4)=2;u(3,6)=5;u(4,5)=9;u(5,3)=6;u(5,6)=10;
num=size(u,1);M=sum(sum(u))*num^2;
[f,val]=mincostmaxflow(u,c)
%求最短路径函数
function path=floydpath(w);
global M num
w=w+((w==0)-eye(num))*M;
p=zeros(num);
for k=1:num
for i=1:num
for j=1:num
if w(i,j)>w(i,k)+w(k,j)
w(i,j)=w(i,k)+w(k,j);
p(i,j)=k;
end
end
end
end
if w(1,num) ==M
path=[];
else
path=zeros(num);
s=1;t=num;m=p(s,t);
while ~isempty(m)
if m(1)
s=[s,m(1)];t=[t,t(1)];t(1)=m(1);
m(1)=[];m=[p(s(1),t(1)),m,p(s(end),t(end))];
else
path(s(1),t(1))=1;s(1)=[];m(1)=[];t(1)=[];
end
end
end
%最小费用最大流函数
function [flow,val]=mincostmaxflow(rongliang,cost,flowvalue);
%第一个参数:容量矩阵;第二个参数:费用矩阵;
%前两个参数必须在不通路处置零
%第三个参数:指定容量值(可以不写,表示求最小费用最大流)
%返回值 flow 为可行流矩阵,val 为最小费用值
global M
flow=zeros(size(rongliang));allflow=sum(flow(1,:));
if nargin<3
flowvalue=M;
end
while allflow<flowvalue
w=(flow<rongliang).*cost-((flow>0).*cost)';
path=floydpath(w);%调用 floydpath 函数
if isempty(path)
val=sum(sum(flow.*cost));
return;
end
theta=min(min(path.*(rongliang-flow)+(path.*(rongliang-flow)==0).*M));
theta=min([min(path'.*flow+(path'.*flow==0).*M),theta]);
flow=flow+(rongliang>0).*(path-path').*theta;
allflow=sum(flow(1,:));
end
val=sum(sum(flow.*cost));调用python库函数方法:
# 最小费用流
L = [(1, 2, 5, 3), (1, 3, 3, 6), (2, 4, 2, 8), (3, 2, 1, 2), (3, 5, 4, 2),
(4, 3, 1, 1), (4, 5, 3, 4), (4, 6, 2, 10), (5, 6, 5, 2)]
G = nx.DiGraph()
for k in range(len(L)):
G.add_edge(L[k][0] - 1, L[k][1] - 1, capacity=L[k][2], weight=L[k][3])
mincostFlow = nx.max_flow_min_cost(G, 0, 5)
print("所求流为:", mincostFlow)
mincost = nx.cost_of_flow(G, mincostFlow)
print("最小费用为:", mincost)






















 8万+
8万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








