[UVa 1394]And Then There Was One

Problem Description

Let’s play a stone removing game.
Initially, n stones are arranged on a circle and numbered 1,…, n clockwise (Figure 1). You are also given two numbers k and m . From this state, remove stones one by one following the rules explained below, until only one remains. In step 1, remove stone m . In step 2, locate the k -th next stone clockwise from m and remove it. In subsequent steps, start from the slot of the stone removed in the last step, make k hops clockwise on the remaining stones and remove the one you reach. In other words, skip (k - 1) remaining stones clockwise and remove the next one. Repeat this until only one stone is left and answer its number.
For example, the answer for the case n = 8 , k = 5 , m = 3 is 1, as shown in Figure 1.

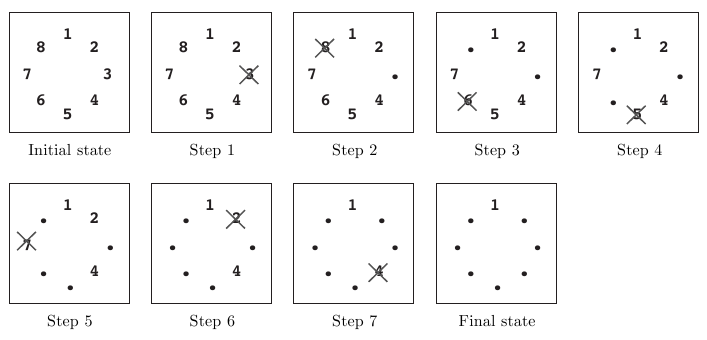
Figure 1: An example game

Initial state:

Eight stones are arranged on a circle.

Step 1:

Stone 3 is removed since m = 3 .

Step 2:

You start from the slot that was occupied by stone 3. You skip four
stones 4, 5, 6 and 7 (since k = 5 ), and remove the next one, which is
8.

Step 3:

You skip stones 1, 2, 4 and 5, and thus remove 6. Note that you only
count stones that are still on the circle and ignore those already
removed. Stone 3 is ignored in this case.

Steps 4-7:

You continue until only one stone is left. Notice that in later steps
when only a few stones remain, the same stone may be skipped multiple
times. For example, stones 1 and 4 are skipped twice in step 7.

Final State:

Finally, only one stone, 1, is on the circle. This is the final state,
so the answer is 1.

Input

The input consists of multiple datasets each of which is formatted as follows.

n k m

The last dataset is followed by a line containing three zeros. Numbers in a line are separated by a single space. A dataset satisfies the following conditions.

2 <=n<=10000, 1<=k<=10000, 1<=m<=n

The number of datasets is less than 100.

Output

For each dataset, output a line containing the stone number left in the final state. No extra characters such as spaces should appear in the output.

Sample Input

8 5 3
100 9999 98
10000 10000 10000
0 0 0

Sample Output

1
93
2019

My Problem Report

一开始拿到这道题很迷茫，能够猜到是由终态，但是一直没法实现状态的转移。后来上网看了题解之后才知道这是著名的Joseph problem（约瑟夫环），在这里总结一下。
这道题其实难并不难在状态转移，而是在于建立状态，或者严格来说是每状态转移过后，对状态的更新。我们以n=8,k=5,m=3为例

n=8时

1 2 3 4 5 6 7 8
1 2 * 4 5 6 7 8

我们对状态进行更新，将每个数减去3，若为负则加上n

-2 -1 0 1 2 3 4 5
6 7 0 1 2 3 4 5

这样我们就把长度为n的约瑟夫环转换为了一个新的长度为n-1的约瑟夫环

1 2 3 4 5 6 7

这时候我们可以发现，原本环中的3转化为了1。我们按这个思路继续往下推，发现到最后新生成的约瑟夫环只剩下一个1。虽然这个1并不代表它在n=8时的标号，但显然我们可以通过从后往前递推得到它原来的标号。
从n=1的状态推导至n=2的状态，设最终剩下的点标号为ans

ans=1
ans=(ans+k%2)%2，若ans为0，ans=2

这样我们就得到了状态在n=2下的x
我们来把这个问题再一般化，设我们将从i-1状态推导至i状态

ans=(ans+k%i)%i，若ans为0，ans=i

这样就求出了我们的递推公式。特别需要注意的是最后一次推导时，k应当取m。

My Source Code

//  Created by Chlerry in 2015.
//  Copyright (c) 2015 Chlerry. All rights reserved.
//

#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <sstream>
#include <cstring>
#include <climits>
#include <string>
#include <vector>
#include <cmath>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <unordered_map>
using namespace std;
#define Size 100000
#define ll long long
#define mk make_pair
#define pb push_back
#define mem(array, x) memset(array,x,sizeof(array))
typedef pair<int,int> P;

int main()
{
    int n,k,m;
while(cin>>n>>k>>m && n+m+k)
{
    int ans=1;
    for(int i=2;i<n;i++)
    {
        ans=(ans+k%i)%i;
        if(!ans) 
            ans=i;
    }
    ans=(ans+m)%n;
    if(!ans) ans=n;
    cout<<ans<<endl;
}

    return 0;
}