趣味三角——第14章——sin(x)=2：虚三角

ComputerInBook

已于 2023-03-06 20:22:04 修改

阅读量910

点赞数 1

分类专栏：数学与应用数学文章标签：复数三角学复三角复三角学三角学三角

于 2023-03-06 20:21:30 首次发布

本文链接：https://blog.csdn.net/ComputerInBook/article/details/129368651

版权

数学与应用数学专栏收录该内容

102 篇文章 13 订阅

订阅专栏

1. 虚数三角学

2. Edmund Landau: 严谨的大师(Edmund Landau: The Master Rigorist)

第14章 sin x = 2: 虚数三角学

(sinx = 2: Imaginary Trigonometry)

De Moivre’s theorem was the key to a whole new world

of imaginary or complex trigonometry。

(De Moivre 定理是通往虚数或复数三角学的全新世界的关键。)

——Herbert Mc Kay, <<The World of Numbers>>(数的世界)

(1946年)，第157页

1. 虚数三角学

设想一下，您刚买了一款全新的手持计算器，当您尝试从4中减去5时，您会发现一个错误信号，这让您很沮丧(dismay)。而这恰恰是一年级的学生，如果老师让他们从四个苹果中拿走五个苹果，他们会发现自己的处境：“做不到！” 将是班级的可预测回应。

数学史上充满了打破“不可能”的障碍的尝试。这些尝试中有许多都以失败告终：两千多年来，数学家们试图仅使用直尺(straightedge)和圆规(compass)来找到一种可将任意角等三等分(trisect)——直到大约在19世纪中叶得到证明，要得出这种结构是不可能的。无数次“化圆为方(square the circle)”的尝试——再次仅用直尺和圆规构建一个面积等于给定圆的正方形——同样被证明是徒劳的(futile),但这并不妨碍业余爱好者提交用于出版的数百个建议的“解决方案”，令数学期刊的编辑们感到沮丧)。

但也有辉煌的成功：负数在数学中的接受使算术从减法的解释中解放出来，作为一种“拿走”的行为，结果是可以考虑一系列全新的问题——从金融问题开始(贷方和借方)求解一般线性方程组。打破禁忌——深深植根于我们的数学本能——反对处理负数的平方根，却为虚数和复数代数铺平了道路，最终形成了强大的复变量函数理论。我们的数字系统的这些扩展的故事，以及它们的许多错误转向和最终的胜利，已经在其他地方讲述过；[1] 这里我们主要关注它对三角学的影响。

我们在三角学学习中首先学习的内容之一便是函数y = sin x 的域是整个实数，范围是区间-1≤ y≤ 1；相应地，如果你试图求得一个角度的正弦值，使其大于1,比如说，等于2，在你使用计算按下arcsin(或者sin-1,或者inv sin),则计算器将会提示一个错误符号——正如在大多数计算器上求

$\sqrt{-1}$ 所出现的错误提示一样。然而,在18世纪初，有人尝试将函数概念扩展到自变量的虚数甚至复数；这些尝试将证明非常成功；其中，它们使我们能够在 y 具有任何给定值(实数、虚数或复数)时求解方程 sin x = y。

Roger Cotes(1682-1716年)便是这方面最早的先驱者之一。在1714年，他发表了这个公式

iΦ = log(cos Φ + isin Φ)

其中， $i=\sqrt{-1}$ ，“log”指自然对数；这在他唯一的主要著作<<Harmonia mensurarum>> 中得以重印，该著作是他去世后于1722年出版的论文汇编。Cotes研究了数学和天文学中的广泛问题(见第82页)，并担任牛顿的“Principia(原理)”的第二版的编辑，但他在34岁那年突然去世，过早地结束了他前途无量的事业；牛顿这样评价他：“如果Cotes还活着，我们可能会知道更多的一些事情(Had Cotes lived we might have known something)。”[2]

毫无疑问，由于Cotes早逝，他从未因发现这一开创性的公式而获得应有的荣誉；它以Euler的名字命名并倒写，

$e^{i\Phi} = cos(\Phi) + i sin (\Phi) ------------------------(1)$

以这种形式，它出现在Euler的伟大著作<<Analysin infinitorum>>(1748年)(无穷小分析)中,与之伴随的还有以下公式

$e^{-i\Phi} = cos(-\Phi) + i sin (-\Phi) = cos(\Phi) - i sin(\Phi)$ 。

通过加减以上这些公式，Euler获得了cos(Φ)和sin(Φ)的如下表达式：

$cos(\Phi) =\frac{e^{i\Phi}+e^{-i\Phi}}{2} , sin(\Phi) = \frac{e^{i\Phi}-e^{-i\Phi}}{2i}-----------(2)$

以上这两个公式是现代解析三角学的基础。

重新发现Cotes公式而给予Euler的荣誉并非完全不值得：Cotes(以及与他同时代的De Moivre)仍然将复数仅仅视为一种方便的(如果说是神秘的话)缩短代数计算的方法，正是Euler将这些数完全纳入“函数(functions)”的代数。他的思想是，假设函数的输出也是复数的话，则复数可以视作函数的输入。

例如，以函数w = sin z为例，其中w和z是复变量。写作z = x + iy，w = u + iv ，继续执行下去，似乎普通的三角学定律仍然成立，我们得到

w = u + iv = sin(x + iy) = sin(x)cos(iy) + cos(x)sin(iy) 。-----------------(3)

但是，cos(iy)和sin(iy)是什么样子，再次以纯粹的公式方式执行下去，我们在等式(2)中，以iy替代Φ:

$cos(iy) = \frac{e^{(i(iy))}+e^{-i(iy)}}{2} = \frac{e^y+e^{(-y)}}{2}$ ,

$sin(iy) = \frac{e^{i(iy)}-e^{-i(iy)}}{2i} = \frac{e^{-y}-e^{y}}{2i} = \frac{i(e^{y}-e^{-y})}{2}$ 。

因此，碰巧的是，表达式 $\frac{e^y+e^{-y}}{2}$ 和 $\frac{i(e^{y}-e^{-y})}{2}$ 分别表现出与函数cos(y)和sin(y)具有许多形式上的相似性,接下来用cosh(y)和sinh(y)表示(读作y的“双曲余弦(hyperbolic cosine)”和“双曲正弦(hyperbolic sine)”):

$cosh(y) = \frac{e^{y}+e^{-y}}{2} , sinh(y) = \frac{e^{y}-e^{-y}}{2}$ 。------------------------------------------------(4)

例如，我们对这两个表达式施行平方，并将结果相减，我们得到恒等式

$cosh^2 (y) - sinh^2 (y) = 1 ,------------------------(5)$

类比于三角恒等式 $cos^2 (y) + sin^2 (y) = 1$ (然而，注意第二项的减法符号)。我们也有cosh(0) = 1 ，sinh(0) = 0，cosh(-y) = cosh(y), sinh(-y) = -sinh(y)，cosh(x±y)= cosh(x )cosh(y )±sinh(x)sinh(y)，sinh(x±y)= sinh(x )cosh(y )±cosh(x)sinh(y),以及d(cosh(y ))/ dy = sinh(y)，d(sinh(y ))/ dy = cosh(y)。事实证明，大多数熟悉的三角函数公式都有对应的双曲函数，其中一项的符号可能会发生变化。[3]

现在我们可以将等式(3)写为

z = sin(x )cosh(y ) + icos(x)sinh(y) --------------------------------------(6)

其中，还是z = x + iy 。以完全相同的方式，我们可以求得cos(z)的表达式：

cos(z) = cos(x )cosh(y ) - isin(x)sinh(y) ---------------------------------(7)

下面举一个例子，让我们求复数的z = 3 + 4i的正弦。所有的单位都采用弧度，我们有sin(3 ) = 0.141, cos(3 ) = -0.990以及sinh(4) = 27.290(所有数值都四舍五入到小数点后三位精度)，因此sin(z)= sin(3)cosh(4 )+ i cos(3) sinh(4) = 3.854 – 27.017 i。

当然，我们刚刚所做的事情有一个严重的缺陷(flaw)：假设当应用于复数时，我们所熟悉的实数代数和三角学定律仍然成立。但确实没有先验(priori)可以确保这些定律对复数也成立。事实上，这些定律有时会在扩展到其原始域之外时失效：例如，对于定律 $\sqrt{a}.\sqrt{a}=\sqrt{ab}$ ,当和是负数时这个定律则不成立，对于其它情况，我们会有 $i^2 = \sqrt{-1}. \sqrt{-1} = \sqrt{(-1)(-1)} = \sqrt{1} = 1$ ，而不是 -1。但这些微妙之处并没有阻止Euler发挥他的新想法：

他生活在一个无忧无虑地操纵符号仍然被接受的时代，并且他充分利用了它。他只是相信他的公式，通常他是对的。他大胆而富有想象力的探索产生了许多新的关系式，其严格的证明必须等待后代去完成。

当然，信念(faith)行为在科学上并不总是可靠指南，尤其是在数学中。复变量函数理论，简称函数论(theory of functions)，正如其简称之意，其创立在某种程度上是为了将Euler的数学思想作为一个坚实的数学基础。我们以这样一种方式来定义一个函数w = f(z):对于函数 y = f(x),当x和y分别被复变量w和z替代时，保留其所有真值(real-valued)的所有性质。此外，当自变量z是实数(即，z = x + 0i )时，作为“新函数”的特例，我们应当总是能回到“旧函数”f(x)。

我们用正弦和余弦函数来例释这几个概念。我们采用等式(6)和等式(7)作为sin(z)和cos(z)的定义，我们可以展示 $sin^{2}(z) + cos^{2} (z) = 1$ ，周其2π(即，对于所有的z,有sin(z+2π) = sin(z)，cos(z)也是类似)，以及我们熟悉的加法公式这几个性质仍然成立。在某种条件下，我们还可以微分复数值函数f(z)；[4] 在这种情况下，我们有d(sin(z))/d z = cos(z), d(cos(z))/d z = -sin(z)，完全与实数情况一样。

但是，您可能会问，如果将实值函数扩展到复数域只是再现了它的旧性质，为什么要这么麻烦呢？如果不是因为这个扩展赋予了函数一些复杂域独有的新性质，那么这肯定是不值得的。其中最重要的一个便是从一个平面映射到另一个平面的概念。

要看到这一点，我们必须首先重新审视应用于复杂变量的函数概念。实值函数 y = f(x) 分配给其域中的每个实数x (“输入”或“自变量”)，并且在其值域中仅分配一个实数 y (“输出”或“因变量”)；因此，它是从x轴到y轴的“映射”。描述此映射的一种简便方法是在xy坐标平面中绘制函数图——本质上是生成一个逞现图形，让我们从字面上看这两个变量相互依赖的行为。

然而，当我们试图将这个想法扩展到复变量时——即将实值函数y = f(x)替换为复值函数 w = f(z)——我们立即遇到了困难。绘制单个复数 x + iy 需要一个二维坐标系——一个坐标表示实部x，另一个坐标表示虚部y。但是现在我们要处理两个复杂变量z和w，每个变量都需要自己的二维坐标系。因此，我们不能像绘制函数y = f(x)一样，“绘制”函数w = f(z)的图像；为了用几何方式描述它，我们需要把它看作是“从一个平面到另一个平面的映射”。

我们用函数 $w = z^2$ 来证明这一点，其中 z = x + yi ，w = u + iv。我们有

$w = u + iv = (x+iy)^{2} = x^2 + 2xyi + (iy)^2 = (x^2 - y^2) + (2xy)i$ 。

使其实部和虚部相等，我们得到

$u = (x^2 - y^2), v = 2xy--------------------(8)$

等式(8)告诉了我们，u和v是两个独立自变量x和y的函数。我们不妨将xy平面称为“z平面”，将uv平面称为“w平面”。则函数 $w = z^2$ 将z平面上的每一个点P(x,y)映射到w平面上对应的点P’(u,v),即P(x,y)的象(image)；例如，点P(3,4)代入公式得 $(3+4i)^2 = -7 + 24i$ ，由此得映射点为P’(-7,24)。现在，设想P描述z平面上的某种曲线；则P’ 描述w平面上的“象曲线(image curve)”。例如，假如P沿着等表达式为 $x^2 - y^2 =$ 常量的等边双曲线(equilateral hyperbola)移动，则P’点将沿着曲线 u = 常量移动, 这是w平面上的一条垂线。类似地，假如P绘制了等边双曲线2xy = 常量的图形，它的象将绘制垂线v = 常量的图形。通过赋予常量不同的值，我们得到了z平面上的两个双曲族；它们的象(images)构成了w平面上的一个矩形网格。(图88)

------------------图88 通过函数 $w = z^2$ 实现的映射-------------------------------------------------

在函数论中，最优雅的结果之一说的是，由函数y = f(z)实现的映射在所有具有非零导数的z点是共形的(保向的(direction reserving))。也就是说，假如z平面上的两条曲线在某一个角(它们在交点处的切线之间的角度)相交，假如d f(z)/d z 存在且在相交点不等于0，则它们在w平面的象曲线也相交于同一个角。对于w = z2 这种情况, 很明显： $x^2 - y^2 =$ 常量和 2xy = 常量这两个双曲线族是正交的(orthogonal)——一个族的每条双曲线都与另一个族的每条双曲线以直角相交——与它们的图像曲线一样，在w平面中,他们的水平线和垂直线也是如此(很显然，互相垂直相交，即以直角相交)。

可以以类似的方式探索由函数w = sin(z)实现的映射。我们以z平面上的水平线 y = c = 常量开始。则等式(6)告诉了我们

u = sin(x )cosh(c )，v = cos(x)sinh(c) ---------------------------------(9)

等式(9)可以视作w平面上描述一条曲线的一对参数方程，参数为x。为了得到这条曲线的矩形方程，我们必须消除这两个等式之间的x。我们可以用cosh(c )除第一个等式，用sinh(c)除第二个等式，将两者平方后再相加；鉴于恒等式 $sin^2x + cos^2x = 1$ ，我们得到

$\frac{u^2}{cosh^2 c} + \frac{v^2}{sinh^2 c} = 1$ 。----------------------------------------------------(10)

等式(10)具有 $\frac{u^2}{a^2} + \frac{v^2}{b^2} = 1$ 的形式，其表示圆心位于w平面坐标原点的椭圆(ellipse),其半长轴(semimajor)a = cosh(c )和半短轴(semiminor) b = |sinh(c )|(因为cosh(y )总是比sinh(y )大——可以从等式(4)推断出来，主轴总是沿着u轴)。然而，请注意，采用一对直线 y = ±c 产生整个椭圆，上半部分对应y = c(其中c > 0),下半部分y = -c (这可以从参数方程中最好地看出[9])。从解析几何我们知道，椭圆的两个焦点(foci)位于点(±f,0),其中， $f^2 = a^2 - b^2$ 。但 $a^2 - b^2 = cosh^2 c - sinh^2 c = 1,$ 因此，我们有f = ±1；因此，对于c取不同的值，无论c取多少，我们都得到一个具有公共焦点对(±1,0)的椭圆族。随着c ->0，cosh(c )->1而sinh(c )-> 0，因此，这个椭圆逐渐变窄，直到它们退化成(degenerate)沿着u轴且位于-1≤u≤1之间的线段。这些特征见图89所示。

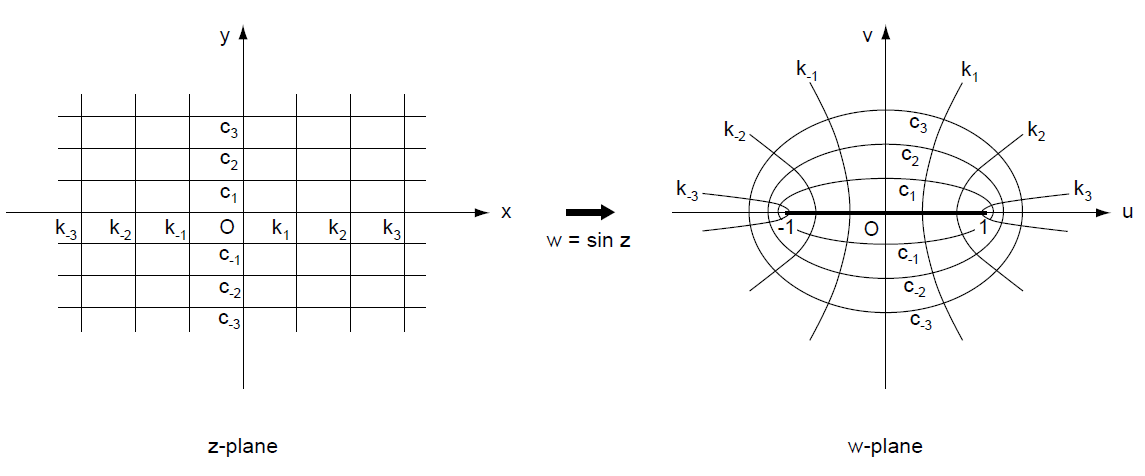
------------------图89 通过函数w = sin(z)实现的映射-------------------------

下一个考虑z平面上的垂线x = k = 常量。等式(9)给到我们

u = sin(k )cosh(y )，v = cos(k)sinh(y) 。---------------------------------(11)

这次我们使用cosh(y)除第一个等式，用sinh(y)除第二个等式,再将结果平方后相减，以消除参数y；鉴于恒等式 $cosh^2 (y) - sinh^2 (y) = 1$ ，我们得到

$\frac{u^2}{sin^2 k}) - \frac{v^2}{cos^2 c} = 1$ 。----------------------------------------------(12)

等式(12)具有 $\frac{u^2}{a^2} - \frac{v^2}{b^2} = 1$ 的形式，其图像是一个中心位于坐标原点，半贯轴(semi-transverse)a = |sin k|以及半共轭轴(semi-conjugate) a = |cos k|的双曲线(hyperbola)；它的渐近线(asymptotes)是直线对 $y = \pm \frac{cos(k)}{sin(k)} x = \pm (cot(k))x$ 。与椭圆一样，它以直线对x = ±k来产生整个双曲线，右分支对应x = k(其中k > 0),左分支x = -k 。双曲线的两个焦点(foci)位于点(±f,0),其中， $f^2 = a^2 + b^2 = sin^2k + cos^2k = 1$ ；因此，改变k的值就产生具有公共焦点对(±1,0)的一族双曲线(见图89)。随着k ->0,对曲线向上张开，且对于k = 0(对应于z平面上的x轴),它们退化成直线z = 0(在w平面上的v轴)。在另一方面，随着| k|递增，双曲线收窄，当 $k =\pm \frac{\pi}{2}$

时，退化成u ≥ 1和u ≤ -1 的一对射线。我们也注意到，按π的幅度递增的任意k都不会改变sin2k或cos2k的值，因此，输出相同的对曲线。当然，这仅仅表明映射不是一对一的，正如我们已经从 sin z 的周期性中知道的那样。最后，椭圆和双曲线形成正交族，正如从复值函数的共形性质推断的那样。[6]

作为更多的一个例子，我们考察函数w = ez，所以我们不妨将复数记为 z = x + iy 并假设实数的代数定律仍然有效：

$e^z = e^{(x + iy)}= e^x. e^{iy}$ 但是， $e^{iy} = cos(y) + i sin(y)$ ,因此，我们有

$e^z = e^x (cos (y) + i sin(y) )$ 。----------------------------------------------(13)

现在，我们将等式(13)作为对 $e^z$ 的“定义”。我们注意到，首先，这不是一个一对一的函数：y按2π递增不会改变 $e^z$ 的值，因此，我们有 $e^{(z + 2\pi i)} = e^z$ 。其次是，复值指数函数ez 具有虚周期(imaginary period)2πi。显然,这与实值函数 $e^x$ 形成了鲜明的对比。写成 $w = e^z = u + iv$ ，等式(13)意味着 $u = e^{x} cos(y), v = e^{x} sin(y)$ 。---------------------------------------(14)

在这些等式中置y = c = 常量，并消除参数x，我们就得到v = tan(c)u，这是从w平面的原点发出的斜率为tan c的射线的方程；置x = k = 常量，并消除参数y，我们得到 $u^2 + v^2 = e^{2k}$ ，这表示中心在原点半径为 $e^{k}$ 的圆。因此，z平面上的矩形坐标网格被映射到w平面上的极坐标网格(polar grid)，呈指数间距的圆圈(图90)。再次地，这两个网格系统处处正交。

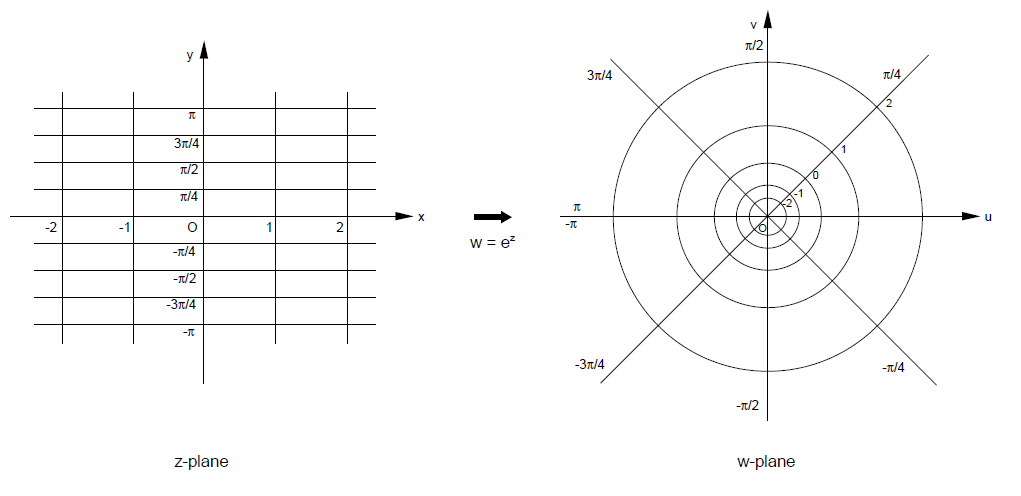
------------------图90 通过函数 $w=e^z$ 实现的映射-------------------------

我们可能会发现这里与上一章讨论的地图投影有意想不到的联系。要在w平面中生成一个极坐标网格，其中圆圈呈线性(而不是指数)间隔，我们必须以对数方式增加k；也就是说，z平面中的垂直线必须间隔为ln k。实现的这个复值函数是函数 $w = e^z$ 的反函数，即 w = ln z 。这种映射，当应用于立体投影的极坐标网格时，给我们的正是Mercator网格——只是水平线和垂直线的角色颠倒了。但是这种反转可以通过将坐标系旋转 90°，即乘以 i 来校正。因此，我们可以从地球开始，将其立体投影到z平面上，然后通过函数 w = i ln z 将该平面映射到w平面上：最终产品是Mercator投影。由于每个组件映射都是共形的，因此它们的产品也是如此。正如我们所记得的，正是这个目标——制作一个基于矩形网格的保形(保向)世界地图——导致Mercator得出他著名的投影。

本章开始时，我们观察到不存在正弦为2的实角。但是既然我们已经将函数sin(x)和 cos(x)扩展到复数域，让我们再试一次。我们希望找到一个“角度”z = x + iy 使得sin(z) = 2。从等式(6)可以得出

sin(x)cosh(y)= 2；cos(x)sinh(y) = 0 。

这些等式中的第二个指的是 sinh(y) = 0 或 cos(x) = 0 ；即，y = 0或 x = (n + 1/2) π，n = 0，±1，±2，... 。在第一个等式中置y = 0得到 sin(x)cosh(0) = sin(x) = 2,因为x是实数，因此这个方程无解。在第一个等式中置 x = (n + 1/2) π，我们得到 $sin[(n + 1/2) \pi]cosh(y)= (-1)^{n} cosh(y) = 2$ ，因此，cosh(y)=±2。但是，cosh(y)的取值范围是[1,∞],与从定义的等式 $cosh(y) = \frac{e^y-e^{(-y)}}{2}$ 所推断的一样；这些可以从具有双曲线功能的表或计算器求得：我们求得y = ±1.317，四舍五入到小数点后三位精度。因此，方程sin(z) = 2 无穷多的解z = (n + 1/2) π ± 1.317i ，n = 0，±1，±2，... 。这些解无一是实数解。

所有这些看起来都非常抽象，与普通的三角学相去甚远；谈论虚角和它们的正弦肯定很奇怪。然而陌生感是一个相对的概念。有了足够的熟悉之后，昨天的“陌生”就变成了今天的司空见惯。当负数开始出现在数学界时，它们最初被认为是奇怪的、人为的创造(“一个人怎么能从四个中减去五个对象呢？”)。类似的反应等待着虚数，正如“虚数”这个名字所证明的那样。当Euler率先将普通函数扩展到复数域时，他的大胆结论既奇怪又充满争议；例如，他是第一个根据虚数定义负数对数的人——这是在虚数的存在还没有被完全接受的时候做出的定义。

权威的高斯(Gauss)将复数完全纳入代数；1799 年，他在21岁的博士论文(doctoral dissertation)中做到了这一点，在论文中，他首次严格证明了代数基本定理(fundamental theorem of algebra)：n 次多项式在复数系统中恰好有n个(不一定互异)根。[7] 当 William Rowan Hamilton爵士(Sir)(1805-1865)在1835年将他对复数的定义优雅地表示为遵守一套正式规则的实数对时，关于这些数“存在性”的任何挥之不去的疑虑都被搁置了。[8] 现在,通向扩展复变量分析的方法的大门已经打开，最终形成函数论(theory of functions)，它在几乎所有数学分支或应用数学分支中都有大量应用。昨天“奇怪”的事，在今天,确实成了家常便饭的事。

注释和资料来源：

1. 关于负数的历史，请参见David Eugene Smith的<<History of Mathematics>>(数学史)( 1925年初版; New York: Dover, 1958年重印)，卷2，第257-260页；关于虚数和复数的历史，同见261-268页。

2. 有关Cotes生活和工作的更多信息，请参阅Stuart Hollingdale的著作<<Makers of Mathematics>>(数学创造者)( Harmondsworth,U.K.: Penguin Books, 1989年出版)第245-252页。

3. 然而，请注意，双曲函数“不是”周期函数，它们的范围是1≤ cosh(y) <∞ 以及-∞≤ sinh(y) <∞ 。“双曲(hyperbolic)”这个名字来自这样一种事实——假如我们写成x = cosh(t),y = sinh(t)(其中，t是实参数),则恒等式 $cosh^2 t - sinh^2 t = 1$ 指的是具有坐标(x,y)的点位于等边双曲线(equilateral hyperbola) $x^2 - y^2 = 1$ 上，就正如坐标为 x = cos(t)，y = sin(t)的一点位于(lies on)单位圆 $x^2 + y^2 = 1$ 上一样。关于双曲函数的故事，请参见我的另一本书 <<e: The Story of a Number>>( e: 一个数的故事)( Princeton, N.J.: Princeton University Press, 1994年出版)第140-150页以及208-210页。

4. 然而，复值函数导数的概念涉及某些不能在实数域中表示的微妙之处。一种折中的方法应归功于德国数学家Karl Weierstrass(1815–1897),他提出，通过采用幂级数来定义函数，对sin(z)而言，定义这个级数为 $z - \frac{z^3}{3!} + \frac{z^5}{5!} + - ...$ 。更多细节，可参见任何关于函数论的书籍。

5. 这是一个影响深远的结果，我们在此仅作了简要说明；有关完整的定理，请参阅任何有关函数论的书籍。

6. 关于映射 w = sin(z)的更多细节的讨论，参见Erwing Kreiszig的著作<<Advanced Engineering Mathematics>>(高等工程数学)( New York: John Wiley,1979)第619-620页。

7. 例如，多项式 $f(z) = z^{3} - 1$ 有3个根，1， $\frac{-1-i\sqrt{3}}{2}$ 和 $\frac{-1+i\sqrt{3}}{2}$ ，正如所见到的那样，因式分解 $f(z) = (z - 1)( z^2 + z + 1)$ ，再置每一个因式为零，再解方程得出其根。这些“单位的立方根(cubic roots of unity)”可以用三角的形式写成cis(0), $cis(\frac{2\pi}{3})$ ，以及 $cis(\frac{4\pi}{3})$

，其中cis代表cos + i sin。学生们总是惊讶地发现数字1有三个立方根，其中两个是复数。

8. 参见Maor的著作<<e: The Story of a Number>>( e: 一个数的故事)第166-168页。

2. Edmund Landau: 严谨的大师(Edmund Landau: The Master Rigorist)

Edmund Yehezkel Landau 1877年出生于柏林；他的父亲是著名的妇科医生(gynecologist)Leopold Landau。他在柏林的法国中学(高中)开始接受教育，此后不久就全身心投入到数学中。Ferdinand Lindemann( 1852–1939)是他的老师之一，他在1882年证明了π的超越性(transcendence)——不能是具有整数系数的多项式方程的根这一事实——从而解决了“化圆为方(squaring the circle)”的这一古老问题(见第181页)。从一开始，Landau就对解析数论(analytic number theory)感兴趣——将解析方法应用于整数研究。 1903年，他给出了一个简化的质数定理(Prime Number Theorem)的证明，该定理在击败 19世纪一些最伟大的思想家之后于七年前首次得到证明。[1] 1909年，年仅31岁的Landau被任命为哥廷根(Göttingen，全称Georg-August-Universität Göttingen)大学数学教授，这里直到二战前都是世界著名的数学研究中心；他接替了Hermann Minkowski(1864-1909 年)，后者以对爱因斯坦相对论的四维解释而闻名，在45岁时去世。Landau发布了超过250篇论文，写了几部关于他自己研究领域的著作，其中就包括 <<Handbook of the Theory and Distribution of the Prime Numbers>>(素数理论与分布手册)(2卷，1909年出版)和<<Lectures on Number Theory>>(数论讲座, 3卷, 1927年出版)。

Landau是应邀在1925年耶路撒冷希伯来大学的落成典礼上发表演讲的八位杰出学者之一。从俯瞰圣城的斯科普斯山顶上，他谈到了“初等数论中已解决和未解决的问题”——对于这样一个喜庆的场合出现的一个相当不寻常的主题。他接受了大学的邀请，担任第一任数学教授，并专门为此自学了希伯来语。他于1927年加入大学，但不久后返回德国继续履行在哥廷根的职责。然而，他辉煌的职业生涯很快就走到了尽头：当纳粹于1933年上台时，他与德国大学的所有犹太教授一起被迫辞去职务。他 1938 年的突然去世使他免于等待德国犹太社区的命运。

Landau体现了纯数学家的终极形象。他蔑视数学的任何实际应用，并避免提及它们，将它们视为Schmieröl(grease(润滑油))；在“实际应用”中是几何学，他完全避开了(shunned from)他的阐述。在他的讲座和书面作品中，定义、定理和证明会接踵而至，丝毫没有暗示其背后的动机。他的目标是绝对且毫不妥协的严谨(rigor)。他的助手总是参与到他的讲课中，他被指示，如果教授遗漏了最细微的细节，他就必须打断并提醒他。[2]

对于高等数学的学生来说，Landau以他的两本教科书而闻名，一本是<<Grundlagen der Analysis>>(Foundations of analysis,分析学基础,1930年出版)，另一本是<<Differential and Integral Calculus>>(微积分,1934年出版)。前者以两篇序言开头，一篇是给学生的，另一篇是给老师的。

给学生的序言是这样开始的：

1. Please don’t read the preface for the teacher.

对于教师，请阅读这则序言。

2. I will ask of you only the ability to read English and to think logically—no high school mathematics, and certainly no higher mathematics.

我只要求你具备阅读英语和逻辑思维的能力——无需高中数学的知识，当然无需具备高等数学的知识。

3. Please forget everything you have learned in school; for you haven’t learned it.

请忘掉你在学校学习的一切；因为你还没有学习它。

4. The multiplication table will not occur in this book, not even the theorem,

本书中不会出现乘法表，甚至连定理也没有，

2.2 = 4;

but I would recommend, as an exercise, that you define

但我推荐，作为练习，你去定义

2 = 1 + 1;

4 = (((1 + 1) + 1) + 1);

and then prove the theorem.

然后去证明定理。

给老师的序言是以这些话结束：

My book is written, as befits such easy material, in merciless telegram style (“Axiom,” “Definition,” “Theorem,” “Proof,”’ occasionally “Preliminary Remark”) : : : : I hope that I have written this book in such a way that a normal student can read it in two days. And then (since he already knows the formal rules from school) he may forget its contents.

我的书是用无情的电报风格(“公理”、“定义”、“定理”、“证明”，偶尔还有“初步评论”)写成的，因为它适合这种简单的材料。: : : 我希望我已经以普通学生两天就能读完的方式写了这本书。然后(因为他已经从学校了解了正式的法则)他可能会忘记它的内容。

然而，不清楚Landau可能会认为谁是“普通学生”，但很难相信普通学生，甚至是数学教授，能够在两天内掌握这本书的301个定理，该定理几乎以象形文字的形式写在这本书的 134页中(图91）。

------------图91 摘自Edmund Landau分析学基础(1930年)一书中的一页-----------

(显然，这是幂级数 $x - \frac{x^3}{3!} + \frac{x^5}{5!} - + ...$ )。这是由定义

定义 59

$sin(x) = \sum_{m=0}^{\infty}\frac{(-1)^{m}}{(2m+1)!}x^{2m+1}$

“sin”读作“sine。” 所推导出的。

在以类似方式定义 cos(x)之后，有几个定理建立了这些函数的熟悉性质。然后

定理258

$sin^2 x + cos^2 x = 1$ 。

证明

$1 = cos(0) = cos(x - x) = cos(x) cos(- x )- sin(x) sin(- x ) = sin^2 x + cos^2 x$

因此，出乎意料且未提及任何名称，引入了最著名的数学定理：毕达哥拉斯定理。

今天，当教科书彼此激烈竞争并且必须畅销才能证明其出版合理时，Landau的教科书能否找到广泛的读者值得怀疑。然而，在战前的欧洲大学中，高等教育是极少数人的特权。此外，教授有权按照他选择的方式教授他的课程，包括选择教材。大多数教授根本遵循任何教材，而是根据自己的讲义(notes)授课，学生可以用其他材料补充这些讲义。在这种氛围下，Landau的教材受到高度评价，因为它为严肃的学生提供了真正的智力挑战。

注释和资料来源：

1. 这个定理说素数的平均密度——给定整数x以下的素数除以x，随着x->∞，这个数趋近于 $\frac{1}{ln(x)}$ ，该定理最早由Gauss于1792年猜想出来，当时他才15岁。它于1896年由法国的Jacques Salomon Hadamard (1865–1963)和比利时的de la Vall´ee-Poussin (1866–1962)独立工作首次证明。

2. 参见Constance Reid所著 <<Courant in Göttingen and New York: The Story of an Improbable Mathematician>>(哥廷根和纽约的Courant：一个不可思议的数学家的故事)( New York: Springer-Verlag, 1976)第25-26页，以及第126-127页。也可参见<<Edmund Landau: Collected Works>>( Edmund Landau作品集)中的文章“In Memory of Edmund Landau: Glimpses from the Panorama of Number Theory and Analysis (缅怀Edmund Landau：从数论与分析的全景中窥见一斑)”，编辑L. Mirsky et al.( Essen: Thales Verlag, 1985)第25-50页。

3. 这两部作品均由Chelsea出版公司翻译成英文：<<Foundations of Analysis: The Arithmetic of Whole, Rational, Irrational and Complex Numbers>>(分析基础：整数、比率数、非比率数和复数的算术)( F. Steinhardt译，1951年)，以及<<Differential and Integral Calculus>>(微积分)( Melvin Hausner和Martin Davis译，1950年)。上面给出的摘录(excerpts)来自英文翻译本。

4. 在他的序言中，Landau为这种方法辩护：“一些数学家可能认为在导数的定义之后给出第二个定理是不正统的(unorthodox)，魏尔斯特拉斯(Weierstrass)定理……, 对他们来说，我要说的是，虽然有一些非常优秀的数学家从未学习过该定理的任何证明，但从他的课本中学习迄今为止最简单的证明对初学者来说并没有什么坏处。”

5. 作为方程cos(x) = 0的最小正解，数π在其下方几行后被引入。然后这个“通用常数”用π表示；没有提到这个常数的数值，也没有提到它与圆的关系。

内容来源：

<<Trigonometric Delights>> 作者：Eli Maor