Fourier分析入门——第14章——Fourier光学

ComputerInBook

已于 2023-06-03 09:22:05 修改

阅读量1.3k

点赞数 1

分类专栏：数学与应用数学文章标签：傅里叶傅立叶光学傅里叶不学

于 2023-06-02 22:57:13 首次发布

本文链接：https://blog.csdn.net/ComputerInBook/article/details/131014098

版权

数学与应用数学专栏收录该内容

102 篇文章 13 订阅

订阅专栏

第14章 Fourier光学

14.1 引言

14.2 物理光学和图像形成(Physical optics and images formation)

14.3 Fourier光学域(The Fourier optics domain)

14.4 图像形成的线性系统描述(Linear Systems Description of Image Formation)

第14章 Fourier光学

14.1 引言

Fourier分析在光学(optics)、光科学(the science of light)和图像(images)科学中起着重要作用。继 20 世纪初期Fourier分析在通信理论和实践中的成功应用之后，光学科学家和工程师在 1950 年代开始采用类似的方法来研究光学系统。在这种新方法中，Fourier分析扮演着几个重要角色。根据图像形成的物理光学理论，由于物平面中的点光源，Fourier变换提供了系统入射光光瞳(entrance pupil)中光的数学分布。同样，Fourier变换也将出射光光瞳中的光分布与像平面中的光分布联系起来，即所谓的点扩散函数(PSF-point spread function)。 Fourier分析也是通信理论方法的核心，在该方法中，光学成像系统被视为线性滤波器，根据物体与系统脉冲响应(PSF)之间的卷积数学运算，线性滤波器将输入信号(物体)转换为输出信号(图像)。模拟这种卷积运算的典型数字计算机程序是采用快速Fourier变换 (FFT) 算法来计算物体的图像。Fourier变换还用于将PSF 转换为称为光学传输函数(OTF-optical transfer function)滤波器作用的空间频域进行描述。要理解为什么Fourier分析在这种现代光学系统方法中发挥如此重要的作用，有必要简要回顾一下图像形成的物理理论。

14.2 物理光学和图像形成(Physical optics and images formation)

图 14.1 所示的图像形成的基本说明是基于几何光学概念，即光沿称为射线(rays)的直线传播。由有限尺寸的物理透镜(lens)捕获的点光源发出的所有光线都会发生折射(refracted)(即它们的传播方向发生变化)。光线(light)的强度(intensity)是由射线(ray)密度(density)决定的，所以光线在密度高的区域会聚就是成像的几何概念。按这种解释，在镜头前引入孔径(aperture)的唯一作用(effect)是限制进入镜头的光线的空间分布。在光圈的边缘，透射光线定义了光影之间的清晰边界，如虚线所示。事实上，正如Newton(1670) 在 17 世纪首次观察到的那样，光确实能穿透阴影。为了考虑这一自然事实，我们必须用更完整的光传播(propagation)和图像形成表述来代替几何光学。

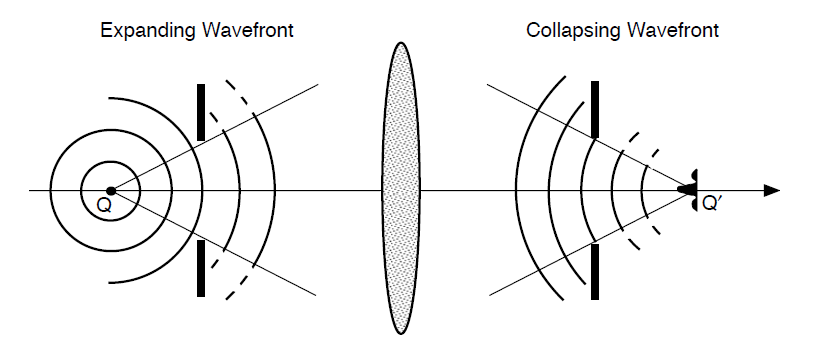
------------------------------图 14.1 孔径的衍射导致光传播到虚线指示的几何阴影中。结果是波阵面失真，即使是完美的镜头也无法形成完美的点阵图像。--------------------

根据物理光学理论，光以垂直于几何光学射线的波的形式传播。波阵面(wavefront或wave front)定义为光从点光源发射后振荡相同时间的轨迹(locus)组成的面(译注：时变波场的波阵面是所有具有相同相位的点的集合(轨迹))。随着每次振荡，光传播一个波长的距离，因此波阵面的等效定义是与点光源具有相同光学距离的点的位置的点组成的面。因此，单点光源发出球面波阵面。与物理上离散的射线不同，波阵面是空间上连续的表面，可能会随着光的传播而扭曲。例如，波阵面通过孔径后，其传播方向在孔径边缘附近略有变化，导致光“泄漏”到光线直线传播预测的阴影区域。这种由孔径阻挡部分波阵面而引起的传播方向和波阵面形状的变化称为衍射(diffraction)(或称“绕射”)。 由于孔径的衍射会扭曲波阵面，因此即使镜头在光学上是完美的，镜头产生的图像也会扭曲。图像中出现这种衍射缺陷的根本原因是，从透镜出现的波阵面只是形成完美点阵图像所需的球面波阵面的一部分。逻辑论证很简单：如果一个单点光源产生一个完整的、扩展的球面波阵面，那么通过反转时间箭头，我们一定推断出——一个完整的、坍缩的球面波阵面需要产生一个单点图像。由于孔径仅传输部分波阵面，因此图像不可能是单点。

------------------------------图 14.2 Huygen的波阵面传播理论--------------------------------------

图 14.2 说明了定量思考传播波衍射的框架。为理解膨胀波(expanding wave)或坍(tān)缩波(collapsing wave)如何传播， Huygens(1678)建议，如果波阵面上的每个点都是新的次级扰动的中心，该次级扰动沿传播方向发出球形子波，则随后任何时刻的波阵面都将是这些次级小波的包络。Fresnel (1818) 通过结合 Young (1801) 对干涉现象的发现提出了现在称为光传播的 Huygens-Fresnel 原理的定量理论，从而改进了 Huygens 的直觉概念。根据这一原理，Huygens的次级小波是定向的(即振幅在垂直于初级波阵面的方向上最强)并且它们相互干涉以重建前进波阵面。因此，当波阵面遇到不透明孔径时，障碍物附近波阵面上的点不再被丢失的Huygens小波抵消，因此光能够在孔径后面传播而不受干扰。随后，Kirchoff (1882)证明Fresnel所做的关键假设(包括Huygens小波的非各向同性性质)是光的波动性质的有效结果。 Sommerfeld (1894) 后来从关于光圈处光的边界值的相互不一致的假设中拯救了 Kirchoff的理论。在这样做的过程中，Sommerfeld将标量衍射理论置于其现代形式中，通过确定衍射现象可以通过线性添加位于孔径本身内的Huygens小波无穷大的振幅来准确解释。在数学上，这种核算采用叠加积分的形式，称为Rayleigh-Sommerfeld衍射公式(Goodman (1968)，方程式 3-26，第 45 页)。如需更全面地了解光的波动理论的历史，请参阅 Goodman，1968，第32页或 Born & Wolf，1970，第xxi-xxviii页。

---------图 14.3 用于计算 S 点Huygens小波对 R 点光源振幅贡献的几何----------

要表达衍射公式，需要对Huygens小波进行数学描述，并需要一种在孔径外的观察点 R 处对它们求和的方法，如图 14.3 所示。尽管严格的理论将光描述为具有根据Maxwell方程耦合的电和磁分量的矢量场，但使用更简单的理论就足够了，该理论将光视为标量现象，其强度随时间呈正弦变化。因此，对于单色波，场强可以写成

u(R ,t) = U(R)cos[2πvt + Φ(R)]--------------------------------------[14.1]

其中，U(R) 和Φ(R) 分别是波在位置 R 时的幅度和相位，而 v 是光学的时间频率。出于数学原因，将三角函数表示为复数指数的实部(见图 2.2)更为方便，方法是将等式[14.1]改写成

$u(R ,t) = Re[U(R)e^{-i2\pi vt} ]$ ---------------------------------------[14.2]

其中， $i=\sqrt{-1}$ , U(R)只是位置的复数值函数，

$U(R) = U(R) e^{-i\Phi(R)}$ -----------------------------------------------[14.3]

场的时间振荡对于衍射问题不是必不可少的，因此我们将相量 U(R) 作为波阵面的数学描述。因此，我们寻求Huygens小波的这种相量描述。单位振幅波阵面任意点 S 所需的函数为

$\mathsf{H}(S ,R) = \frac{1}{i\lambda } \frac{e^{-ikr}}{r} cos(\theta)$ ----------------------------------------[14.4]

其中，

H = 由于 S 处的Huygens小波而引起光在R 处的复振幅

r = 从源点 S 到观察点 R 的辐射距离

k = 2π/λ ，波数，将 r 转换为以弧度为单位的相移

λ = 光的波长

θ = RS 线与 S 处波阵面法线(normal,始终垂直于平面的虚线)之间的夹角

等式 [14.4] 右侧的三个因素中的每一个都与Huygens小波的一个基本特征有关。中间因子是点源引起的球面波阵面的标准表达式。该因子的分子(numerator)说明了小波从 S 传播到 R 时产生的相移，分母(denominator)说明了随着波阵面扩展而保持总能量恒定所需的振幅损失。这个球面小波由第一个因子修正，即二次源的振幅比一次波小 1/λ 倍，二次源的相位超前一次波的相位 90°。等式[14.4]中的第三个因素是倾斜因子，它表示次级小波的振幅随 S 处波前法线与观察点 R 相对于 S 的方向之间的角度 θ 的余弦而变化。

等式[14.4]描述了由单位幅度的初级波阵面产生的次级小波。将实际波阵面振幅 U(S) 作为加权因子，S 点的小波为 U(S)H(S,R) 的乘积。然后通过将孔径 A 内的所有次级小波引起的场线性叠加来找到点 R 处的总场。结果是孔径上的叠加积分

$U(R) = \iint \limits_{aperture}\mathsf{U}(S)\mathsf{H}(S,R)dAU(R)$ --------------------------------------[14.5]

这就是 Rayleigh-Sommerfeld 衍射积分，(Goodman,1968, 45页, 方程 3-28)。

14.3 Fourier光学域(The Fourier optics domain)

在某些受限情况下，等式 [14.5] 的叠加积分简化为卷积积分。这立即表明Fourier分析的卷积定理(Bracewell，1969）的应用，它将给定的量 U 和 H 转换为对应的一对新量，从而提供衍射和光学图像形成的互补视图。这是Fourier光学的领域。

首先，竖立一个以图 14.3 所示的孔径为中心的坐标参考系，𝗑、𝗒 平面与孔径平面重合。R 处的观察点坐标为 ( 𝗑, 𝗒, 𝗓 )，孔径平面中的任意点坐标为 (𝗑', 𝗒', 0 )。最初的简化假设是源远离孔径，因此波前几乎是平面的，观察点 R 也远离孔径并靠近 𝗓 轴，在这种情况下，方程[14.4]中的倾斜因子 cos(θ)大约为 1。在这些假设下，等式分母中的距离 r 。 [14.4] 可以用 𝗓 代替。但是，这不是分子中的有效替换，因为此近似值中的任何误差都会乘以一个大数 k 。为了解决这个问题，我们需要更详细地研究 r 如何依赖于 S 和 R 的坐标。根据Pythagoras定理，

$r = \sqrt{(x'-x)^{2}+(y'-y)^{2}+z^{2}}$ ---------------------------------------------------[14.6]

使用多项式展开的前面两项，上式可以近似为

$r = z + \frac{(x'-x)^{2}+(y'-y)^{2}}{2z}$ --------------------------------------------------------------------[14.7]

将这些近似应用到等式[14.4]产生如下针对Rayleigh-Sommerfeld的近似公式

$H( x ',y ', x, y, z ) = \frac{1}{i\lambda z}\mathsf{exp}\{ik[z + \frac{(x'-x)^{2}+(y'-y)^{2}}{2z}]\}$ ---------------------------[14.8]

(译注： exp 表示以 e为底的指数函数记法。)

关于这个公式需要注意的重点是，虽然 H 是观察点的 (𝗑, 𝗒) 坐标和源点的 (𝗑', 𝗒') 坐标的函数，但这种依赖性仅取决于两者坐标之间的差异(difference)，而不是取决于它们的绝对值。因此，Huygens小波在光瞳平面(pupil plane)中的绝对位置并不重要。这是必须将等式[14.5]的Rayleigh-Sommerfeld叠加积分解释为卷积积分的特殊情况。潜在的简化假设称为Fresnel(近场)近似。

为了进一步简化卷积积分，我们将等式[14.7]展开，并将每个项按物理意义的方式分组。

$r = z+\frac{x'^{2}+y'^{2}}{2z}+\frac{x^{2}+y^{2}}{2z}+\frac{xx'+yy'}{z}$ ----------------------------------------------[14.9]

如果我们假设孔径不仅比观察距离 z 小，而且比 z/k 小，那么等式 [14.9] 中的第二项可以省略。这个假设被称为 Fraunhofer(远场)近似，并且它显然是一个严格的假设，因为 k是一个非常大的数，对于可见光来说大约为 $10^{7}m^{-1}$ 。例如，对于 1mm 的孔径半径，观察距离 z 必须在 5m 或更远的数量级。在这种情况下，从光圈到远距离观察点 R 的光程长度的最大差异约为 0.1 微米(约为可见光波长的 1/6 )，表示光的时间振荡的相对相移约为 1 弧度。在这些限制条件下，Rayleigh-Sommerfeld 衍射积分简化为

$\mathsf{U}(x , y) = C \iint \limits_{aperture}\mathsf{U}(x',y')\mathsf{exp}\{-\frac{ik}{z}(xx'+yy')dx'dy' \mathsf{U}(R)\}$ ----------[14.10]

为了使这个结果用起来更方便，我们将(𝗑, 𝗒)坐标规范化，引入变量替换 $\hat{x}=x/\lambda z$ , $\hat{y}=y/\lambda z$ 。我们也可以引入光瞳函数P(𝗑', 𝗒'),其在孔径内有一个值为1，在孔径外有一个值为0。使用这个光瞳函数作为被积函数中的倍增因子，我们可以定义整个孔径平面上的积分，在这种情况下，等式[14.10]变成了

$\mathsf{U}(\hat{x} ,\hat{y}) = C \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \mathsf{P}(x',y')\mathsf{U}(x',y')\mathsf{exp}[-2 \pi idx'(\hat{x}x'+\hat{y}y')dx'dy' \mathsf{U}(R)]$ -----------------[14.11]

假如最后一个积分看起来不熟悉，将 𝗑', 𝗒' 看成是光瞳平面上的空间频率变量，且将 𝗑, 𝗒 看成是图像平面上的空间变量。现在，除了前面的尺度常量C ，Fraunhofer 衍射图案被认为是入射波阵面U被光瞳函数 P 截断时的二维Fourier逆变换。当入射波阵面是均匀平面波时，这个看似不可思议的(miraculous)结果又产生了另一个惊人的观察结果。在这种情况下，场振幅 U(𝗑', 𝗒') 在孔径上是恒定的，因此衍射图案 $\mathsf{U} (\hat{x} ,\hat{y})$ 和孔径 P(𝗑', 𝗒') 通过Fourier变换相关联 . 此Fourier变换操作的紧凑符号使用箭头指示正向Fourier变换的方向

$\mathsf{U}(\hat{x},\hat{y})= \begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}P( x', y')$ ---------------------------------------------------------[14.13]

换句话说，等式 [14.13] 表示，由于孔径对单色平面波的衍射，远平面中光分布的振幅 U 与孔径的光瞳函数 P 的Fourier逆变换成正比。相反，孔径的光瞳函数 P 与远场光分布 U 的正向Fourier变换成正比。

等式 [14.12] 在 20 世纪下半叶对包括视觉光学在内的光学科学和工程产生了重大影响，因为它带来了强大的线性系统理论及其主要计算工具Fourier变换(Goodman， 1968 年；Bracewell，1969 年；Gaskill，1978 年；Williams & Becklund，1989 年)。尽管使用衍射图样的语言，等式[14.12] 很容易应用于成像系统，方法是将光瞳函数的概念概括为包括透镜的聚焦特性。通过将光瞳函数视为二维滤波器，它会衰减振幅并在出现的波阵面的每个点引入相移，复数值的光瞳函数 P( 𝗑', 𝗒')可以构造为两个因子的乘积，

P( 𝗑', 𝗒') = D ( 𝗑', 𝗒') exp{ikW ( 𝗑', 𝗒')}-----------------------------------------------[14.14]

其中 D ( 𝗑', 𝗒') 是衰减因子，W ( 𝗑', 𝗒') 是称为波像差函数(wave aberration function)的相位因子，它直接归因于系统的聚焦像差。这种推广光瞳函数的操作捕捉了光学系统的效果，而没有违背导致等式[14.13]发展的论点。因此，对于远点光源，包括衍射和干涉效应在内的像差光学系统像平面中的复数值振幅扩展函数 A(𝗑, 𝗒) 等于系统光瞳函数的Fourier逆变换 ,

$\mathsf{A}(x,y)= \begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}P( x', y')$ ----------------------------------------------------------[14.15]

这种重要关系的图形描述如图 14.4 a、c 所示。

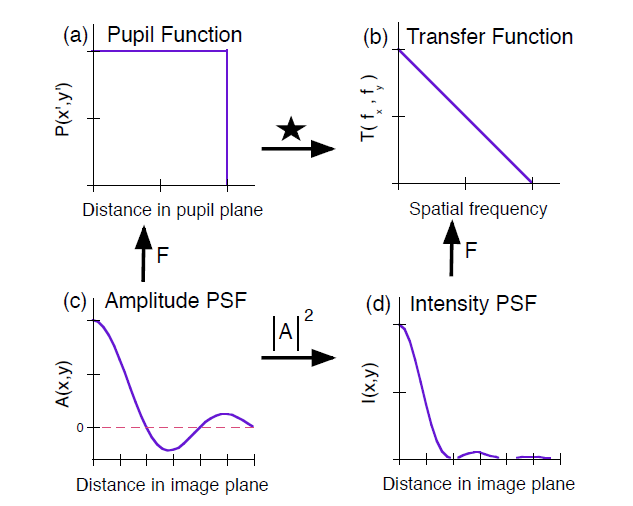
---------图 14.4 与光学成像系统相关的基本量之间的Fourier关系的示意图。实际函数是二维空间域上的表面。(a, b, c) 是复数值函数，(d) 是实数值函数。------------

光的物理探测器，包括眼睛中的视杆细胞和视锥细胞，不能足够快地响应以跟随光振幅的快速时间振荡。取而代之的是，物理传感器对光强度(intensity)做出响应，光强度是一个实数值量，定义为复振幅的平方模量的时间平均值。因此强度 PSF 由下式给出

$I(x,y) = | A(x,y)|^2 = A(x,y) A^* (x,y)$ ----------------------------------[14.16]

其中， $A^*$ 表示 A 的复数共轭，这个重要关系的图形描述见图14.4 c,d 所示。

综合起来，等式[14.15] 和 [14.16] 表示强度 PSF，它是眼睛光学系统成像能力的基本描述，是眼睛光瞳函数的Fourier逆变换的平方模。下一节显示光瞳函数也可用于推导眼睛成像系统的另一个基本描述符，即光学传输函数。正如将要展示的，这两个描述符都可以使用Fourier变换以直接的方式计算任意对象的视网膜图像。

14.4 图像形成的线性系统描述(Linear Systems Description of Image Formation)

20 世纪光学的主要范式(paradigm)转变之一是将成像系统(包括眼睛)作为空间域中由 PSF(point spread function)表征的线性系统进行处理。 (有关历史记录，请参见 Williams & Becklund，1989)。图像是聚焦良好还是模糊、衍射受限或畸变都无关紧要。关键假设很简单，PSF 对于点源的横向(即与光轴正交)平移是不变的。在线性系统理论中，这种性质称为空间不变性(space invariance)，但在光学中称为等晕现象(isoplanatism)。线性系统方法对眼睛的特殊意义在于，它使我们能够根据 PSF 的知识和物体强度的空间分布轻松计算实际的视网膜图像(外部观察者通常无法访问)。

尽管眼睛的 PSF 在整个视野中变化很大，但假设视网膜图像的小块(small patches)具有空间不变性并非不合理。在这样的小块中，图像被认为是无数(myriad) PSFs 的叠加，PSF对应于对象中的每个点，并根据对象中相应点的强度按比例缩放强度。对于普通物体，从物体上不同点发出的光波的相位之间没有固定的关系。这种光源被称为空间不相干，对于这种光源，视网膜图像中基本 PSF 的强度是线性相加的实数值量。因此，视网膜图像可以由叠加积分表示，在空间不变性的假设下，叠加积分等效于卷积积分。用❊表示卷积运算，我们可以用一个简单的数学关系来概括成像过程

spatial image = spatial object * PSF--------------------------------------------[14.17]

等式[14.17]的一个应用的例子是计算具有 4 毫米光瞳的眼睛遭受 1 屈光度散焦的预期视网膜图像，如图 14.5 所示。出于计算目的，假定本例中的大写字母对着 1/3 度的视角，对于从 57 厘米处观看的 3.3 毫米字母、从 40 厘米处观看的普通新印刷品或字母在验光师视力表的 20/80 线上。使用具有 3 mm 光瞳的眼睛查看此大小文本的计算视网膜图像的其他示例和光学像差的各种数量和组合如图 14.6 的下行所示。为了进行这些计算，使用了 van Meeteren 的波像差函数在屈光度方面的幂级数展开式(van Meeteren，1974)。 这些结果表明，光学像差的影响可能会使视网膜图像模糊(blur)、污损(blur)或加倍，具体取决于存在的像差类型及其大小。

---------图 14.5作为对象(左)与眼睛的点扩散函数(中间，放大以显示细节)的卷积的视网膜图像(右)的示例计算。------------

在线性系统Fourier分析的一般理论中，任何输入函数(例如光学对象)、输出函数(例如光学图像)或性能函数(例如光学PSF)在频域中都有对应物。 在光学中，这些分别对应于物体的频谱、图像的频谱和光学传输函数(OTF)。根据定义，OTF是空间频率的复数值函数，其大小等于图像对比度与物体对比度之比，其相位等于图像与物体之间的空间相位差。 OTF 的这两个分量分别称为调制传输函数 (MTF，modulation transfer function) 和相位传递函数 (PTF，phase transfer function)。

---------图 14.6具有与图 14.5 中相同的角度大小的单个字母的模糊示例。字母高度 = 视角的 1/3 度，光瞳直径 = 3mm，D = 散焦屈光度，DC = 散光屈光度，DSA = 球差屈光度。------------

对应的空间和频率函数对之间的联系由Fourier变换建立。例如，强度 PSF 和 OTF 是Fourier变换对，

$I(x,y)= \begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}T( x', y')$ ------------------------------------------------[14.18]

这种重要关系的图形描述如图 14.4 b、d 所示。等式[14.18]的物理基础源自这样一个事实，即在频域中，基本对象不是一个光点，而是一个正弦光栅图案。按照这种思维方式，视觉目标不是由许多光点的排列来定义的，而是由许多光栅的叠加来定义的，每个光栅具有不同的空间频率、对比度和方向。鉴于单个光点具有无限延伸的平坦Fourier光谱，构成点对象的图像相当于同时构成无限数量的光栅的图像，每个光栅具有不同的频率和方向但具有相同的对比度和相位。在这种情况下形成图像光谱与物体光谱的比率是微不足道的，因为物体光谱是恒定的。因此，每个分量光栅的图像对比度和空间相位的变化，表示为空间频率的函数，将是系统 OTF 的有效描述。因此，PSF 表示光学系统如何在图像平面中散布光，包含有关系统如何衰减对比度和移动组件光栅相位的潜在信息。根据等式[14.18]，可以通过应用Fourier变换来恢复这种潜在信息。

等式 [14.17] 的输入输出关系的频率解释需要Fourier理论的一个重要结论，称为卷积定理。该定理指出，一个域中两个函数的卷积等价于另一个域中相应函数的乘法(参见第 12.2 章节)。将该定理应用于等式[14.17]将频域中的成像过程归结为复值对象频谱和复值 OTF 的乘积，

image spectrum = object spectrum·OTF--------------------------[14.19]

鉴于上述结果，可以得出两个重要结论。第一个是PSF和光瞳函数之间的Fourier变换关系。作为初步步骤，使用卷积定理和复数共轭定理(Bracewell，1969)结合等式[14.15]

计算两个域中振幅扩展函数的平方模量。

$\mathsf{A}(x,y) \begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}\mathsf{P}( x', y')$

$\mathsf{A^*}(x,y) \begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}\mathsf{P}( -x', -y')$

$\mathsf{A}(x,y)\mathsf{A^*}(x,y) \begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}\mathsf{P}( x', y')*\mathsf{P}( -x', -y')$ --------------------------[14.20]

通常将这种卷积关系转化为自相关关系，用五角星 (★) 符号表示 (Bracewell, 1969, 第112, 122页)，使用规则

$P ( x', y')* P^* (- x', -y') = P ( x', y')\bigstar P ( x', y')$ -----------------------[14.21]

将等式 [14.16], [14.20], 和 [14,21] 结合在一起，得到

$I(x,y) \begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}\mathsf{P}( x', y')\bigstar \mathsf{P}( x', y')$ --------------------------------------------[14.22]

换句话说，等式[14.22]指的是，强度PSF是光瞳函数自相关函数的逆Fourier变换。

我们可以从前面的发展中总结出的第二个结论是，完成了图 14.4 中绘制的关系矩阵。因为 OTF(等式 14.18)和光瞳函数的自相关(等式 14.22)都是 PSF 的Fourier变换，所以它们必须彼此相等。

$I(x,y)\begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}\mathsf{T}( x', y')$

$I(x,y)\begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}\mathsf{P}( x', y')\bigstar \mathsf{P}( x', y')$

$\mathsf{T}( x', y')\begin{matrix} \overset{FT} \longrightarrow \\ \underset{FT^{-1}} \longleftarrow \end{matrix}\mathsf{P}( x', y')\bigstar \mathsf{P}( x', y')$ ----------------------------------------------[14.23]

这种重要关系的图形描述如图 14.4 a、b 所示。最后一个结果光瞳函数置于成像系统频率分析的核心，就像成像系统的空间分析一样。它也适用于极其重要的几何解释，因为光瞳函数的自相关等效于光瞳函数与其自身的移位副本的重叠区域。

实际上，要使用前面的结果，需要仔细注意光瞳平面中 (𝗑', 𝗒') 坐标参考系的比例(参见 Goodman，1968 年，第 117 页)。处理这个缩放问题的最简单方法是在制定光瞳函数的解析表达式时通过光瞳半径对光瞳坐标进行归一化。然后，在所有计算完成后，可以利用衍射设置的截止空间频率 $f_C$ 将频率尺度转换为物理单位

$f_C = d/\lambda$ (周期/弧度(光瞳中心角的角度)) --------------------------------------[14.24]

其中，d是光瞳直径，λ 是波长。按照惯例，OTF 的幅度在零空间频率下始终为一，这是通过按光瞳面积对光瞳函数的幅度进行归一化来实现的。例如，在无像差系统中，光瞳函数在光瞳内的值为 1，在光瞳外的值为 0。对于具有圆形光瞳的系统，例如眼睛，等式 [14.23] 的 OTF 只是两个圆的重叠面积作为它们重叠的函数，由圆的面积归一化。由对称性，其结果仅随着辐射空间频率 $f_r=\sqrt{f_x^2+f_y^2}$ (Goodman, 1968; 等式6-31)。

$\mathsf{T} ( f ) = \frac{2}{\pi}cos^{-1} ( f ) - f\sqrt{1-f^{2}}],....f = f_r / f_C$ ----------------------[14.25]

总之，光瞳函数(图 14.4a)、PSF(图 14.4d)和 OTF（图 14.4b）是光学系统(例如眼睛)的非相干成像特性的相互关联的表征。其中，光瞳函数是最基本的，因为它可以用来导出其他两个函数。然而，通常情况下情况并非如此，因为图 14.4 中所示的自相关运算和平方模运算缺乏可逆性，因此无法从 PSF 或 OTF 计算出唯一的光瞳函数。还应该记住，上面回顾的理论没有考虑散射光的影响，因此必然是不完整的。

内容来源：

<< Fourier Analysis for Beginners>> Larry N. Thibos