Description
Given four points ABCD, if ABCD is a tetrahedron, calculate the inscribed sphere of ABCD.
Input
Multiple test cases (test cases



 ).
).
Each test cases contains a line of 12 integers








 indicate the coordinates of four vertices of ABCD.
indicate the coordinates of four vertices of ABCD.
Input ends by EOF.



 ).
).
Each test cases contains a line of 12 integers









 indicate the coordinates of four vertices of ABCD.
indicate the coordinates of four vertices of ABCD.
Input ends by EOF.
Output
Print the coordinate of the center of the sphere and the radius, rounded to 4 decimal places.
If there is no such sphere, output "O O O O".
If there is no such sphere, output "O O O O".
Sample Input
0 0 0 2 0 0 0 0 2 0 2 0
0 0 0 2 0 0 3 0 0 4 0 0
Sample Output
0.4226 0.4226 0.4226 0.4226
O O O O
题意:
有一个以ABCD点为顶点的四面体 求 这个四面体的内接球的球心坐标和半径(取四位小数)
T_T 终于发现不学好高数的坏处,我会努力学习高数的.
首先判断 四个点是否面 如果是 直接输出"O O O O"
判断四个点是否共面 我是用了混合积
我判断是<=esp 代表他们四点共面 注意计算的时候 要算出绝对值
如果不共面的话 就开始算内接球的球心和半径
四面体的体积 是等于上面求的混合积再除以6
内接球的半径公式
V是体积 S是四面体的表面积
所以我们还要求出四面体的表面积
四个表面积用向量积求出来
然后求坐标
Si 是指 当前Pi作为顶点所对的面的面积 S是四面体的表面积
上述四面体的公式. 百度均可得到
其余的向量积,混合积,看高数课本就好
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
const double esp=1e-8;
struct point
{
double x,y,z;
point (double xx=0,double yy=0,double zz=0)
{
x=xx;
y=yy;
z=zz;
}
friend point operator -(const point &a,const point &b)
{
return point(a.x-b.x,a.y-b.y,a.z-b.z);
}
}p[4];
//算出 法向量的 坐标 然后 根号(x^2+y^2+z^2) *0.5就是这个面的面积
double cross(point p1,point p2)
{
return sqrt(pow(p1.y*p2.z-p1.z*p2.y,2)+pow(-(p1.x*p2.z-p1.z*p2.x),2)+pow(p1.x*p2.y-p1.y*p2.x,2));
}
//注意加上绝对值 会可能算出负数
double vol(point p1,point p2,point p3)
{
return fabs((p2.y*p3.z-p2.z*p3.y)*p1.x-(p2.x*p3.z-p2.z*p3.x)*p1.y+(p2.x*p3.y-p2.y*p3.x)*p1.z);
}
int main()
{
while (~scanf("%lf%lf%lf",&p[0].x,&p[0].y,&p[0].z))
{
for (int i=1 ; i<4 ; i++)
scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].z);
double V=vol(p[1]-p[0],p[2]-p[0],p[3]-p[0]);
if (V<=esp)
{
printf("O O O O\n");
continue;
}
V=V/6;
double s1=0.5*cross(p[1]-p[0],p[2]-p[0]);
double s2=0.5*cross(p[1]-p[0],p[3]-p[0]);
double s3=0.5*cross(p[2]-p[0],p[3]-p[0]);
double s4=0.5*cross(p[1]-p[2],p[3]-p[2]);
double S=s1+s2+s3+s4;
double r=V*3/S;
double x=(p[0].x*s4+p[1].x*s3+p[2].x*s2+p[3].x*s1)/S;
double y=(p[0].y*s4+p[1].y*s3+p[2].y*s2+p[3].y*s1)/S;
double z=(p[0].z*s4+p[1].z*s3+p[2].z*s2+p[3].z*s1)/S;
printf("%.4f %.4f %.4f %.4f\n",x+esp,y+esp,z+esp,r+esp);
}
return 0;
}










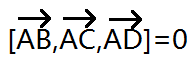
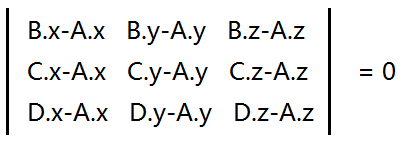
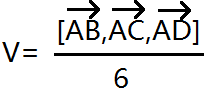


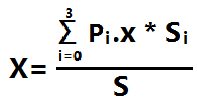
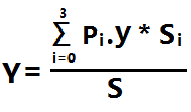
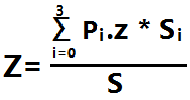
















 2663
2663

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








