LTI系统的频域分析法

一般信号应该如何分解，傅里叶级数还是傅里叶变换？基本信号作为激励时，LTI系统如何响应？一般信号作为激励时，LTI系统如何响应？频域分析法的原理、工具、步骤、优缺点是什么？这是本文致力阐述的问题。

1. 基本信号 $e^{j\omega t}$ 作用于LTI系统的响应

设LTI系统的冲激响应为 $h(t)$, 当激励是角频率 $\omega$ 的基本信号 $e^{j\omega t}$ 时，其响应（频域分析中，基本信号的定义域是在负无穷到正无穷区间内的，而在负无穷处可以认为系统的状态为0， 因此这里的响应指的是全响应，也等于零状态响应）为：
$$y(t)=h(t)\ast e^{j\omega t}$$
根据卷积定义，得：
$$y(t)={\int }_{-\infty }^{\infty }h(\tau ){\mathrm{e}}^{j\omega (t-\tau )}\mathrm{d}\tau ={\int }_{-\infty }^{\infty }h(\tau ){\mathrm{e}}^{-j\omega \tau }\mathrm{d}\tau \cdot {\mathrm{e}}^{j\omega t}$$
$h(t)$ 的傅里叶变换，记为 $H(j\omega )$ ，常称为系统的频率响应函数，也称为传输函数：
$$H(j\omega )=\mathrm{F}[h(t)]={\int }_{-\infty }^{\infty }h(\tau ){\mathrm{e}}^{-j\omega \tau }\mathrm{d}\tau$$
所以，基本信号 $e^{j\omega t}$ 作用于LTI系统的响应为：
$$y(t)=H(j\omega )\cdot e^{j\omega t}$$
显然， $H(j\omega )$ 反映了响应 $y(t)$ 的幅度和相位。

2. 一般信号 $f(t)$ 作用于LTI系统的响应

基本信号 $e^{j\omega t}$ 作用于LTI系统的响应可表示为：
$$e^{j\omega t}⟹H(j\omega )e^{j\omega t}$$
由齐次性：
$$\frac{1}{2\pi }F(j\omega )\mathrm{d}\omega e^{j\omega t}⟹\frac{1}{2\pi }F(j\omega )\mathrm{d}\omega H(j\omega )e^{j\omega t}$$
由可叠加性：
$$\frac{1}{2\pi }{\int }_{-\infty }^{\infty }F(j\omega )e^{j\omega t}\mathrm{d}\omega ⟹\frac{1}{2\pi }{\int }_{-\infty }^{\infty }H(j\omega )F(j\omega )e^{j\omega t}\mathrm{d}\omega$$
由傅里叶逆变换的公式可知，上式左侧即为 $f(t)$ ；而上式右侧为 $H(j\omega )F(j\omega )$ 的傅里叶逆变换，所以上式可以表示为：
$$f(t)⟹F^{-1}[H(j\omega )F(j\omega )]$$
因此，一般新号 $f(t)$ 作用于LTI系统的响应为：
$$y(t)=F^{-1}[H(j\omega )F(j\omega )]$$
对 $y(t)$ 进行傅里叶变换有：
$$Y(t)=H(j\omega )F(j\omega )$$
所以可以这么描述：对于一般信号 ，其作用于LTI系统的响应的傅里叶变换为该新号的傅里叶变换与系统的传输函数（频率响应函数）的乘积。这不正是 时域卷积对应频域相乘 吗？

3. 傅里叶变换分析法

从上面可知，在求一个系统的响应时，可以分为下面4个步骤来完成:

1. 求输入信号 $f(t)$ 的傅里叶变换 $F(j\omega )$ ;
2. 求系统的传输函数（频率响应函数）；
3. 求零状态响应 $y(t)$ 的傅里叶变换 $Y(j\omega )=H(j\omega )F(j\omega )$ ;
4. 求 $Y(j\omega )$ 的傅里叶逆变换 $y(t)=F^{-1}[H(j\omega )F(j\omega )]$ .

4. 傅里叶级数分析法

无论是周期信号还是非周期信号我们均可以采用傅里叶变换来进行频域分析，但是周期信号也可以用傅里叶级数来进行频域分析。因此，如果掌握了傅里叶变换分析法，按道理来说就足够了。但是也不能说傅里叶级数分析法鸡肋，因为有时候工程追求的是最优解法，所以多掌握几种方法肯定是不错的。

4.1 指数形式的傅里叶级数

周期信号 $f_T(t)$ 的指数形式的傅里叶级数可以表示为：
$$f_T(t)=\sum _{n=-\infty }^{\infty }{F}_n{\mathrm{e}}^{jn\Omega t}$$
系统的零状态响应可以表示为：
$$y(t)=h(t)\ast f_T(t)=\sum _{n=-\infty }^{\infty }{F}_n\left[h(t)\ast e^{jn\Omega t}\right]=\sum _{n=-\infty }^{\infty }{F}_{n}H(jn\Omega )e^{jn\Omega t}$$
上式中， $F_{n}H(jn\Omega )$ 即为系统的零状态响应 $y(t)$ 的傅里叶系数。

因此，傅里叶级数分析法也可以总结为以下4个步骤：

1. 求周期输入信号 $f_T(t)$ 的傅里叶系数 $F_n$ ;
2. 求系统的传输函数（频率响应函数）离散化后的取值序列 $H(jn\Omega )=H(j\omega ){|}_{\omega =n\Omega }$；
3. 求零状态响应 $y(t)$ 的傅里叶系数 $F_{n}H(jn\Omega )$ ;
4. 求傅里叶级数的展开式 $y(t)$ .

4.2 三角形式的傅里叶级数

周期信号 $f_T(t)$ 的三角形式的傅里叶级数可以表示为：
$$f_T(t)=\frac{A_0}{2}+\sum _{n=1}^{\infty }{A}_n\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathrm{n}\mathrm{\Omega }\mathrm{t}+{\phi }_{\mathrm{n}}\right)$$
系统的传输函数还可以表示为模值和相角相乘的形式：
$$H(j\omega )=|H(j\omega )|e^{j\theta (\omega )}$$
那么传输函数在傅里叶级数基频和各谐频处的离散化取值为：
$$H(jn\Omega )=|H(jn\Omega )|e^{j\theta (n\Omega )}={H(j\omega )|}_{\omega =n\Omega }$$
类比指数形式表达的零状态响应，容易得到当周期信号作为激励时，系统的零状态响应为：
$$y(t)=\frac{A_0}{2}\underset{\text{直流增益 }}{\underbrace{H(0)}}+\sum _{n=1}^{\infty }\underset{\text{幅值相乘 }}{\underbrace{A_n\mid H(jn\Omega )\mid }}\cos [n\Omega t+\underset{\text{相位相加 }}{\underbrace{{\varphi }_n+\theta (n\Omega )}}]$$

5. 实践（做题是掌握概念的有效检验方式）

若某LTI系统的幅频特性 $|H(j\omega )|$ 和相频特性 $\theta (\omega )$ 如下图所示，若激励为 $f(t)=2+4\cos (5t)+4\cos (10t)$ , 如何求系统的响应？

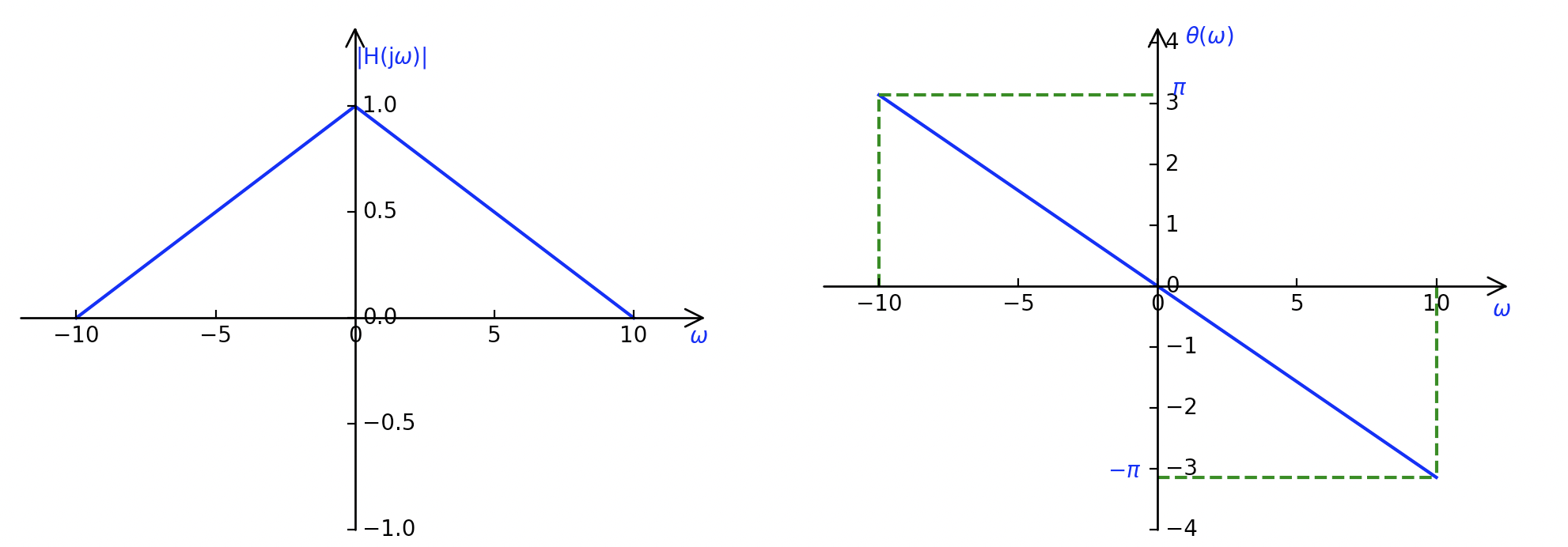
下面将分别用傅里叶级数分析法和傅里叶系数分析法来求解系统响应。

5.1 傅里叶变换分析法解答

系统的传输函数是已知的，为：
$$H(j\omega )=|H(j\omega )|e^{j\theta (\omega )}$$
激励函数 $f(t)$ 的傅里叶变换为：
$$F(j\omega )=4\pi \delta (\omega )+4\pi [\delta (\omega +5)+\delta (\omega -5)]+4\pi [\delta (\omega +10)+\delta (\omega -10)]$$
则可以求出响应的傅里叶变换为：（把下面式子中的分数都变成小数）
$$\begin{array}{rl}Y(j\omega )& =F(j\omega )H(j\omega )\\ & =4\pi \delta (\omega )+4\pi \cdot \delta (\omega +5)\cdot H(-5j)+4\pi \cdot \delta (\omega -5)\cdot H(5j)+4\pi \cdot \delta (\omega +10)\cdot H(-10j)+4\pi \cdot \delta (\omega -10)\cdot H(10j)\\ & =4\pi \delta (\omega )+4\pi \cdot 0.5\cdot e^{0.5\pi }\cdot \delta (\omega +5)+4\pi \cdot 0.5\cdot e^{-0.5\pi }\cdot \delta (\omega -5)+0+0\\ & =4\pi \delta (\omega )+j\cdot 2\pi \cdot \delta (\omega +5)-j\cdot 2\pi \cdot \delta (\omega -5)\end{array}$$
因为正弦函数 $\sin \left({\omega }_{0}t\right)$ 的傅里叶变换为：
$$\sin \left({\omega }_{0}t\right)=\frac{1}{2j}\left({\mathrm{e}}^{j{\omega }_{0}t}-{\mathrm{e}}^{-j{\omega }_{0}t}\right)⟷j\pi \left[\delta \left(\omega +{\omega }_0\right)-\delta \left(\omega -{\omega }_0\right)\right]$$
所以，对 $Y(j\omega )$ 进行傅里叶逆变换，可以得到响应为：
$$y(t)={\mathrm{F}}^{-1}[Y(j\omega )]=2+2\sin 5t$$

5.2 傅里叶级数分析法解答

激励函数的基波角频率为 $\Omega =5\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$ , 所以激励函数可以写为：
$$f(t)=2+4\cos (\Omega t)+4\cos (2\Omega t)$$
观察易得：
$$H(0)=1,H(j\Omega )=0.5{\mathrm{e}}^{-j0.5\pi },H(j2\Omega )=0$$
根据本文公式可以直接求得响应为：
$$\begin{array}{rl}y(t)& =\frac{A_0}{2}H(0)+\sum _{n=1}^{\infty }{A}_n|H(jn\Omega )|\cos \left[n\Omega t+{\varphi }_n+\theta (n\Omega )\right]\\ & =2\times 1+4\times 0.5\cos (\Omega t-0.5\pi )+4\times 0\\ & =2+2\sin 5t\end{array}$$

本文首发于微信公众号 振动信号研究所