这两天零零散散的看了一些数论方面的知识,在这里做一个小小的总结
关于取模运算的一些性质和定理
- 基本性质
- 若p|(a-b),则a≡b (% p)。例如 11 ≡ 4 (% 7), 18 ≡ 4(% 7)
- (a % p)=(b % p)意味a≡b (% p)
- 对称性:a≡b (% p)等价于b≡a (% p)
- 传递性:若a≡b (% p)且b≡c (% p) ,则a≡c (% p)
运算规则
模运算与基本四则运算有些相似,但是除法例外。其规则如下:- (a + b) % p = (a % p + b % p) % p
- (a - b) % p = (a % p - b % p) % p
- (a * b) % p = (a % p * b % p) % p
- a ^ b % p = ((a % p)^b) % p
- 结合律:
- ((a+b) % p + c) % p = (a + (b+c) % p) % p
- ((a*b) % p * c)% p = (a * (b*c) % p) % p
- 交换律:
- (a + b) % p = (b+a) % p (7)
- (a * b) % p = (b * a) % p (8)
- 分配律:
- (a+b) % p = ( a % p + b % p ) % p (9)
- ((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p
- 重要定理
- 若a≡b (% p),则对于任意的c,都有(a + c) ≡ (b + c) (%p)
- 若a≡b (% p),则对于任意的c,都有(a * c) ≡ (b * c) (%p)
- 若a≡b (% p),c≡d (% p),则 (a + c) ≡ (b + d) (%p),(a - c) ≡ (b - d) (%p)
- (a * c) ≡ (b * d) (%p),(a / c) ≡ (b / d) (%p)
- 基本性质
- 欧拉公式
- 欧拉函数计算的是小于等于n的数中与n互质的数的数目。
- 通式
φ(x)=x(1−1/p1)(1−1/p2)...(1−pn)
- 其中p1, p2……pn为x的所有质因数,x是不为0的整数。
- φ(1)=1(唯一和1互质的数(小于等于1)就是1本身)。
- 注意:每种质因数只一个。 比如12=2*2*3那么φ(12)=12*(1-1/2)*(1-1/3)=4
- 若n是质数p的k次幂,则φ(n)=p^k-p^k-1,因为除了p的倍数外,其他数都跟n互质
- 欧拉函数是积性函数——若m,n互质,φ(mn)=φ(n)*φ(m)
- 特殊性质:当n为奇数时,φ(2n)=φ(n)
- 若n为质数则φ(n)=n-1
- 代码实现
- 通式
- 欧拉函数计算的是小于等于n的数中与n互质的数的数目。
int F[MAX_N];
void Euler_function()
{
for (int i=2;i<MAX_N;i++)
{
if(F[i]==0)
{
F[i]=i-1;
for(int j=2*i;j<MAX_N;j+=i)
{
if(F[j]==0)F[j]=j;
F[j] =F[j]/i*(i-1);
}
}
}
}- 欧拉定理
- 如果a,n互素,则有
其中当n本身是素数时有a^(p-1) ≡ 1 (mod p)
应用:可以用于求m^n当m和n都很大时的尾数,例题LightOJ 1282
- 如果a,n互素,则有
- 欧几里得算法
- 作用:求a,b的最大公约数gcd(a,b)=gcd(b,a%b)
- 代码实现:
int gcd(int a,int b)
{
int t;
while(b!=0)
{
t=b;
b=a%b;
a=t;
}
return a;
}- 扩展欧几里得算法
- 作用:用于解不定方程ax+by=gcd(a,b)
- 代码实现:
int exGcd(int a,int b,int &x,int &y)//注意这里x,yx是引用下
{
if(b==0)
{
x=1;y=0;
return a;
}
int r=exGcd(b,a%b,x,y);//因为要使用到回溯后的x,y值,所以不能用循环模拟实现
int t=x;x=y;y=t-a/b*y;
return r;
}- 快速幂
- 作用:用于快速求解x^k
- 代码实现:
int Quike_pow(const int &x,int k)
{
if(k==0)return 1;
else
{
int y=Quike_pow(x,k/2);
if(k&1)
return y*y*x;
else return y*y;
}
}注:以上部分文字摘自百度百科








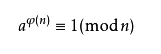
















 747
747

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








