目录
一、什么是感知机?
1958年,美国心理学家Frank Rosenblatt提出一种具有单层计算单元的神经网络,称为感知机(Perceptron)。感知机模拟人的视觉接受环境的信息,并利用神经元之间的连接进行信息传递。在感知机的研究中首次提出自组织、自学习的思想,而且对所能解决的问题存在着收敛算法,即在数学上能严格证明有效,因而对神经网络的研究起了重要的推动作用。
由于单层感知机的结构和功能都非常的简单,以至于目前在解决实际问题时很少被采用,但是由于它在神经网络研究中具有重要的意义,是研究其他深度网络的基础,所以理解单层感知机的原理是必要的。
二、单层感知机模型
单个人工神经元模型(M-P模型):
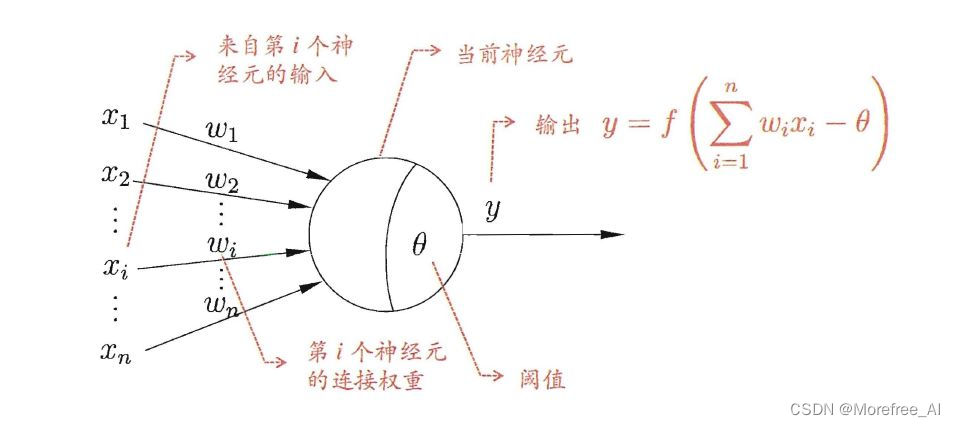
多输出节点的单层感知机:
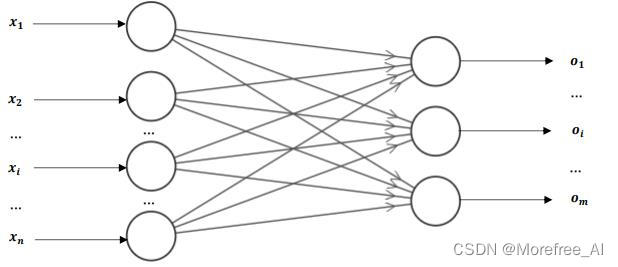
单层感知机只有一层处理单元,结构如上图所示。
图中左侧为输入层,也称为感知层,有n个神经元节点,这些节点只负责引入外部信息,自身不进行信息的处理。每个神经元节点接受一个输入信号(
=1,2,3…n),n个输入信号构成输入列向量
:
图中右侧为输出层,也称为处理层,有m个神经元节点。每个节点均具有信息处理能力,m个节点向外输出处理过的信息构成输出列向量:
对于输出层来讲,用表示输出层第
个神经元的权值列向量,其中
。
m个权值列向量又构成了感知机的权值矩阵。
其中元素为,表示输入层第
个神经元到输出层第
的神经元的权值。
(表示下一层即输出层的第
个神经元,
表示上一层即输入层的第
个神经元。)
由M-P模型可知,对于输出层的任意一神经元节点,其输入
,
为神经元
的阈值,净输入为
,激励函数为符号函数
。则输出神经元
的输出
表示为:
在计算神经元的输出时,实际为一个M-P模型,其中输入向量
,权值向量
,则
展开写成标量形式为:
这在几何意义上实则为一个n维超平面的一般方程,为超平面的法向量,
为超平面的截距。此n维超平面可以将n维空间分为两个部分,也即可以将输入的样本分为两类。
关于以上几何意义说法的简要证明:
因为过空间一点可以作而且只能作一平面垂直于一已知直线,所以当平面上一点
和它的一个法线向量
为已知时,平面
的位置就完全确定了。由此我们可以建立平面
的方程:
设是平面
上的任意一点,
为平面上已知一点,则向量
必然与平面的法线向量
垂直,即数量积等于零:
因为,
,所以有:
此方程是由平面上已知一点和该平面的法线向量
确定的,所以该方程叫做平面的点法式方程。
由上可知,平面的点法式方程是x,y,z的一次方程,而任意一平面都可以用它上面的一点及法线向量来确定,所以任一平面都可以用三元一次方程来表示。设有一般三元一次方程:
任取满足该方程的一组数,即
上述两式相减,得
方程和上面的点法式方程作比较,可知方程
即为点法式方程,而方程
又和方程
经过加减已知的
可以互相得到,所以方程
和
是同解方程。由此可知,任一三元一次方程的图形总是一个平面,而其中x,y,z的系数就是该平面的法线向量
,即
。
上述的证明限制在三维空间中,可以用三元一次方程表示。而在上述列向量所确定的n维空间中,亦可以用
的n元一次方程确定一个n维超平面:
同理,变量的系数就是该超平面的法向量。
上述的证明可以更好的从几何的意义上理解单层感知机具有分类能力,且只能解决线性的二分类问题。
三、感知机的学习策略
假设训练数据集是线性可分的,感知机的学习目标就是确定一个能够将训练集正实例点和负实例点完全分离的超平面,也就是将训练集的输入正确地分类到+1和-1两个类别中。
所以需要确定感知机的参数:权值向量和阈值
(几何意义上的超平面截距)和定义一个损失函数(loss function)并将损失函数极小化。
分类问题损失函数的确定的一个自然想法是:误分类点的个数。使误分类点的个数达到最少即完成了感知机的分类目标。但是这样的损失函数是离散的,并不是参数和
的连续可导函数,所以不易进行优化求取极小值。
另一个损失函数选择是:误分类点到超平面的总距离。(因为可能有多个被误分类的点,所以这里的“总”指的是它们的距离之和。)误分类点到超平面的总距离越小,即代表被误分类的点越少。这是感知机所采用的损失函数。
在三维空间中,点到平面
的距离表示为:
这里不再给出点到平面的距离公式证明。同理,将此距离公式推广到n维空间,则n维空间中样本点到超平面
的距离为:
这里的就等价于模型的输入向量。其中
为权值向量
的
范数,即向量的模长。
对于模型的输入,输出为:
激励函数(即符号函数)会将输入映射为两类输出标签,即输出
对于误分类数据来说,输入结果被分到-1标签,即
;输入
,结果却被分到+1标签,即
。那么有以下式子恒成立:
那么根据以上分析,误分类的样本点到超平面的距离是:
设误分类样本点集合为,且不考虑
,就得到了感知机的损失函数:
显然,损失函数是非负的。没有误分类点是损失函数是零。有误分类点时,误分类点越少,误分类点离超平面越近,损失函数的值就越小。
四、感知机的学习算法
感知机的学习问题就是求解损失函数的最优化问题,方法是随机梯度下降法。首先求出损失函数的梯度:
再随机选取一个误分类点,用
表示迭代次数,
表示学习率,对
和
进行迭代更新:
这种学习算法几何上的直观解释为:当一个样本点被误分类时,即位于超平面的错误一侧时,则根据上式迭代调整和
,使超平面向该误分类点的一侧移动,以减少误分类点和超平面的距离,直至迭代到合适的
和
使得超平面越过该误分类点使其被正确分类。
例题:有某数据集,其正实例点为,
,负实例点为
,学习率
,求感知机模型
。
解:(1)首先随机选取初值:,
(2)判断实例点是否被正确分类:
对,
,未被正确分类,迭代
(3)对于新的和
确定的新的超平面,再次判断实例点是否被正确分类:
对,
,被正确分类;
对,
,被正确分类;
对,
,未被正确分类,迭代
重复(2)(3)过程,直至三个实例点都被正确分类,得到最终迭代结果:
,
即最终所确定的感知机模型为:
分离超平面为:
例题代码:
import numpy as np
import matplotlib.pyplot as plt
train = [((3,3),1),((4,3),1),((1,1),-1)]
feature = []
label = []
xpoints=[]
ypoints=[]
for data in train:
feature.append(data[0])
label.append(data[1]) #提取特征和标签数据
xpoints.append(data[0][0])
ypoints.append(data[0][1]) #提取x,y坐标用于后面的画图
feature = np.array(feature)
label = np.array(label) #将特征和标签数据转化为numpy数组
w = np.array([0,0])
b=0
eta = 1 #初始化w,b,eta学习率设为1
flag = True #设置标记用于结束迭代
num = 0 #记录迭代次数
while flag:
count = len(feature)
for i in range(len(feature)):
if -label[i]*( np.dot(w,feature[i].T) + b) >= 0: #如果数据被误分类
w = w + eta*label[i]*feature[i].T
b = b + eta*label[i]
num = num + 1
print("第{}次迭代:w={},b={}".format(num,w,b)) #迭代并输出迭代后的w和b
else:
count = count - 1 #conut循环减1,减到0时表示所有数据都分类成功
if count == 0:
flag = False #如果所有数据都分类成功。停止循环迭代
print("共迭代{}次,最终迭代结果:w={},b={}".format(num,w,b)) #输出最终结果
x = np.linspace(-5,+5,50)
y = -(w[0]*x + b)/w[1]
plt.plot(x,y)
plt.plot(xpoints,ypoints,'o',)
plt.show() #画出示意图输出结果:
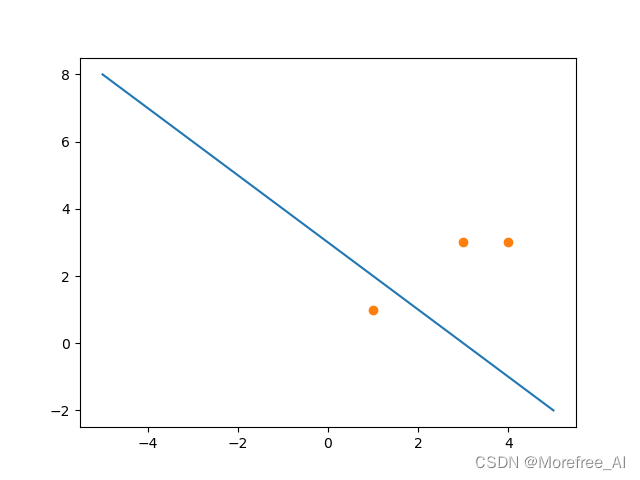
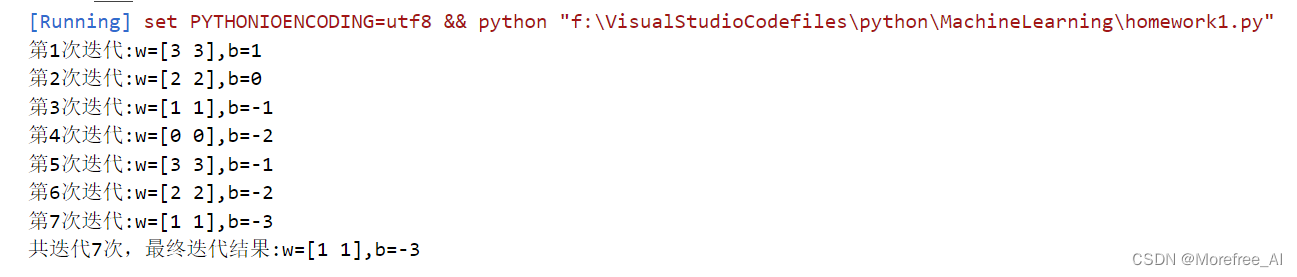
注:不同的参考书中,对于输入可能写成或
。对于
还是
的问题,由于本文章输入是由M-P模型(单个神经元模型)引入的,所以这里采取前者的写法。采取后者写法甚至更优,会使迭代公式有统一的形式,即:
而前者写法的迭代公式为:
两种写法并无本质的不同,所得最终结果也是一样的,后者写法虽然更优,但不再做更改,需要读者尤其注意正负号的问题。
参考
[1]刘若辰,慕彩虹,焦李成,刘芳,陈璞花.人工智能导论[M].北京:清华大学出版社,2021.8:195-200.
[2]李航.统计学习方法[M].北京:清华大学出版社,2019.5:35-41.
[3]同济大学数学系.高等数学[M].北京:高等教育出版社,2014.7:23-27.

























 3620
3620

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










