LeetCode：翻转二叉树

1、题目描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

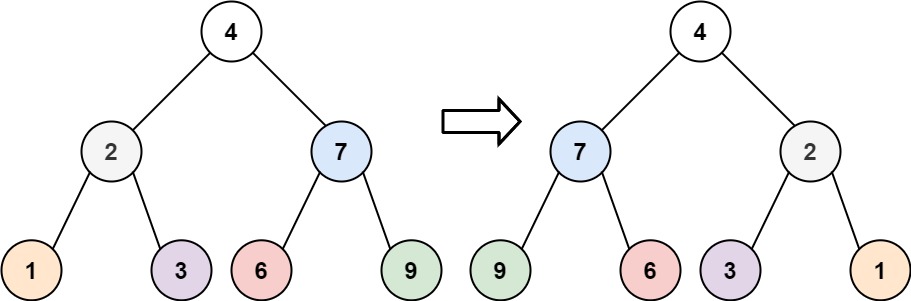
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内

• -100 <= Node.val <= 100

2、方法1：递归法

核心思想：采用分治思想，先处理子树再处理根节点

1. 递归到最左叶子节点

2. 递归到最右叶子节点

3. 从底部开始逐层交换左右子树

4. 最终返回完成翻转的根节点

public TreeNode invertTree(TreeNode root) {
    if(root == null) return null;
    invertTree(root.left);   // 递归翻转左子树
    invertTree(root.right);  // 递归翻转右子树
    swap(root);             // 交换当前节点的左右子节点
    return root;
}

复杂度分析：

• 时间复杂度：O(n) 每个节点访问一次

• 空间复杂度：O(h) 递归栈空间（h为树高）

3、方法2：迭代法（层序遍历+队列）

核心思想：广度优先遍历，逐层交换节点

1. 使用队列实现BFS（广度优先）遍历，逐层交换

2. 每访问一个节点立即交换其左右子节点

3. 子节点入队前已完成交换，保证后续正确处理

public TreeNode invertTree(TreeNode root) {
    if (root == null) return null;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()){
        TreeNode node = queue.poll();
        swap(node);  // 核心交换操作
        if (node.left != null) queue.offer(node.left);
        if (node.right != null) queue.offer(node.right);
    }
    return root;
}

复杂度分析：

• 时间复杂度：O(n)

• 空间复杂度：O(w) w为树的最大宽度

4、方法3：迭代法（后序遍历+栈）

核心思想：用栈模拟递归过程，显式控制遍历顺序

1. 维护pre指针标记已访问的右子树

2. 只有确保左右子树都访问后才执行交换

3. 严格遵循左→右→根的处理顺序

public TreeNode invertTree(TreeNode root) {
    if(root == null) return null;
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root, pre = null;
    while (cur != null || !stack.isEmpty()){
        while (cur != null){
            stack.push(cur);
            cur = cur.left;
        }
        cur = stack.pop();
        if (cur.right == pre || cur.right == null){
            swap(cur);      // 后序位置交换
            pre = cur;
            cur = null;
        } else {
            stack.push(cur);
            cur = cur.right;
        }
    }
    return root;
}

复杂度分析：

• 时间复杂度：O(n)

• 空间复杂度：O(h)