完全搞懂匈牙利算法原理

打点计时器

于 2025-03-20 16:06:23 发布

阅读量914

点赞数 14

文章标签：算法

本文链接：https://blog.csdn.net/DaDianJiShiQi/article/details/146388075

版权

匈牙利算法是计算机经典算法之一，但网上很少有讲原理的，自己看原文梳理了一遍，原文完整地展现匈牙利算法的数学推导和程序设计的思路，非常经典。整理不易希望看官们给个赞^_^。

《The Hungarian Method for the Assignment Problem》原文pdf：https://www.math.toronto.edu/mccann/1855/KuhnNRL55.pdf

1.匹配问题

“匹配问题”是指，用得分来表示n个人对n份工作的匹配程度，将这n个人分配到n个工作，如何使所获得的得分之和尽可能大。这个问题的解决思路是在两位匈牙利数学家的工作上可以衍生出来的，所以叫做“匈牙利算法”。

“匹配问题”可以看成是，在大小为n乘n的表格中，每行每列选定一个数值，使得它们的总和最大，如下图。

“匹配问题”也可以看成是，图论中二部图（Bipartite graph）的最大匹配问题。二分图被划分为两个部分（下图左、右），每个部分内的点互不相连。匹配是边的集合，任意两条边不能有共同的顶点。

2.简单匹配问题

从简单的情况开始讨论：
有四个工人(i = 1,2,3,4)可匹配四个工作(j= 1.2,3,4)，他们的匹配资格信息因资格矩阵Q表示，其中行代表个人，列代表工作，当工人i能匹配工作j时，，否则。

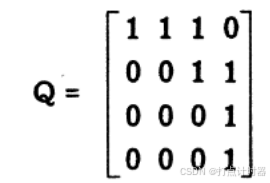
用矩阵Q来描述简单匹配问题：
在同一行或同一列不能有两个1被选中的情况下，最多能从Q中选出1的个数是多少?

先将未配对的工人安排在符合条件的未配对工作中，可以给定一个初始的匹配结果，已确定的配对用星号标记。

这个“匹配结果”，已经不能通过新增匹配（将未配对工人安排在符合条件的未配对工作中）来继续优化，此时称匹配结果是“完全的”（complete）（也叫完美匹配）。

如果一个匹配结果已经是完全的，就可以尝试通过“转移”（transfer）来改进，例如，将工人1从工作3移动到工作1。这次转移会将匹配结果从“完全匹配”变成“不完全匹配”:

接着，可以将个人3或个人4安排到未分配工作4来新增一个匹配，得到的匹配结果是最优的。

在得到“最优匹配”（ optimal assignment）后，可能还存在“转移”，例如，工人1从工作1移动到工作2，或者工人1从工作2移动到工作1 等，但是，这些转移后得到的匹配结果都还是“完全匹配”。

可以得出结论：简单匹配问题总是可以通过连续的“转移”和“新增匹配”来持续优化匹配结果，直到匹配结果不可能再优化，就得到了一个“最优匹配结果”。

最优匹配的充分条件

结合上面的结论可以得到判断最优匹配的充分条件：
定理4：给定一个“匹配结果”，如果所有可能的转移都产生“完全匹配结果”，则可以判断，这个“匹配结果”是最优的（因为已经无法通过新增匹配或转移进行改进）。此时，对于每个可能的（已确定或未确定）配对来说，或者配对人是关键的，或者配对工作是关键的，或者两者都是关键的。（证明见第6节）

关键行和关键列

将转移进行一般化的定义：

一次转移指的是，对原本r个已匹配到工作上的人 $i_1,...,i_r$ ，将移动到未配对工作中，接着按顺序将移动到中。其符号如下：

把转移中的工人，定义为关键人（essential individual），也叫关键行。

把（n个工作中）已经配对且配对人不是关键人的工作，定义为关键活（essential job），也叫关键列。

任何一个已（确定）配对只有两种情况，要么可以转移，要么不能转移。对于一个已配对里的这个人和这个工作来说，如果已配对可转移，那么，人是关键人，工作是非关键；如果已配对不能转移，那么，人是非关键人，工作是关键工作。

所以，在任何情况下都有，已配对数=关键人数+关键活数。

对偶问题的充分性质

从对偶问题的角度来看待简单匹配问题。

在对偶问题里，给每个工人、每个工作分配一个单位的预算（budget）或不分配预算。

在一个“预算（分配）结果”中，如果对每个可能的配对，它的工人或工作两者中有一个或两者被给予了预算，那么称为“预算结果”就是充分的（adequate）。

预算分配问题问到：如何花费最少的预算使得所有可能的匹配都充分。

因为每个配对中的人或工作至少有一个算进了预算，且配对总数总是不少于已配对数量，显然可知：

定理3。任何一个“充分预算结果”的预算总量不少于最大已配对总数。

这里要回顾一下定理1，给定一个“匹配结果”，如果所有可能的转移都产生“完全匹配结果”，此时“匹配结果”是最优的。此时，对于每个可能的（已确定或未确定）配对来说，或者配对人是关键的，或者配对工作是关键的，或者两者都是关键的。接着，给每个配对只分配一个单位预算（关键人、关键活两者其中一个），则它的“预算结果”是充分的，并且因为已配对数=关键人数+关键活数，所以它的预算总数等于它的已配对总数，即最大匹配总数。

所以有定理4：存在一个“充分预算结果”，它的预算总数等于它的已配对总数。

结合定理3和定理4可以得到对偶问题的充分性质：对于任何一个“充分预算结果”，赋予了预算的匹配集合一定包括了至少一个“最优匹配”的匹配集合。一个“充分预算结果”可能对应多个“最优匹配结果”。

简单匹配问题的解

结合最优匹配结果的充分条件和对偶问题的充分性质，简单匹配问题的结论如下：

对于一个给定的“匹配结果”，当且仅当在每种可能的转移下都可以得到“完全匹配结果”时，这个“匹配结果”是最优的，此时，已配对总数达到最大，且等于对偶问题“充分预算结果”的最小预算总数。

3.广义匹配问题

假设有n个工人和n份工作，给出评分矩阵，是不包括0的正整数。一个“匹配结果”是工人和工作的一对一配对。所以，在广义匹配问题的任意一个匹配结果中，所有工人和工作都是已配对，“匹配结果”可以表示为一个1到n排列的形式，一行是工人序号，一行是工作序号：

广义匹配问题问到：怎样匹配能使的值最大？

考虑对偶问题的“充分预算结果”：对于每一个已确定的配对，给予该配对的工人和工作的预算和不低于该配对的评分。令一个已配对中，给予工人的预算为，给予工作的预算为，评分为，写成符号：

广义匹配问题的对偶问题问到：在“充分预算结果”中，预算总数的最小值是多少？

和简单匹配问题同理，可以得到以下结论：

定理5。任意一个“充分预算结果”的预算总数不少于任意一个“匹配结果”的评分总数。

证明：因为在一个“充分预算结果”的“匹配结果”中，每个配对中工人和工作只计算其中一个，也就是一个配对只计算一次评分，而预算总数是每个配对中工人和工作的预算这两个评分可能都进行计算，也就是一个配对可能会计算两次评分，所以不会后者不会少于前者。用符号表示，在“充分预算结果”的条件下，有：

这些不等式相加可得：

整数排列是的一个排列。定理5得证。

由此得出，如果一个“充分预算结果”的预算总数等于它的一个“匹配结果”评分总数，那么此时它们必定同时是匹配问题和其对偶问题的解。

接下来我们将证明这个解总是存在的，并且可以通过求解一个确定的、与之相关的简单匹配问题来得到这个解。

关联简单匹配问题

对于广义匹配问题的一个“充分预算结果”，它的关联匹配问题（associated Simple Assignment Problem）的定义如下：

关联简单匹配问题。如果，则称工人i和工作j简单已配对，否则为简单未配对。（为了更好的区分，将原问题的已匹配称为广义已匹配、未匹配为广义未匹配）。

给定一个“充分预算结果”，存在两种可能的情况：

（1）如果它的关联简单匹配问题里，n个工人和n个工作全部都简单已配对，那么此时的“匹配结果”和“预算结果”是广义匹配问题的解，并且广义已配对的评分总数等于预算总数。

（2）如果它的关联简单匹配问题，不是n个工人和n个工作全部是简单已配对，则此时的“预算结果”可以通过一个步骤来继续优化，这个步骤是：关键人的预算不变、非关键人的预算减一、关键活的预算加一、非关键活的预算不变。

根据这个步骤，可以将所有评分/配对格子分为4种情况：

这个步骤的可以重复次数由非关键人非关键活的格子决定，因为要保证每个格子的预算（人的预算+活的预算）大于评分，所以这个步骤的最大下降空间是这些非关键人非关键活的格子中下降空间（预算减去评分）的最小值。

由此可以得出结论：

定理7。给定一个“充分预算结果”，对于它的关联简单匹配问题，如果最多有m<n个已确定的配对，则预算总量一定可以下降一个正整数量。

广义匹配问题的解

从任意一个“充分预算结果”开始（简单地，可以从每个人给予最大预算、每个工作不给予预算开始），如果此时不是最优，由定理6可知，那么就可以通过定理7来进行预算总量的下降优化。因为这种优化是有限次数的，所以可以得到广义匹配问题的解如下：

在广义匹配问题中，可以通过连续求解有限个关联简单匹配问题来得到最优解，此时，评分总和达到最大，并且等于任意一个“充分匹配结果”的最小预算总量。

4.匈牙利算法

本节汇总前两节的结果，并明确阐述前面论证中隐含的算法。

1）先创建一个初始覆盖：

在线性规划里，将广义匹配问题的“充分预算结果”称为“覆盖”（cover）。

如果，每行需要按列顺序检验，每行里面的头一个没有星号的1标记上星号。如果，行列互换角色进行同样的操作。

令，。

然后令，，。

2）用一个矩阵来表示关联简单匹配问题矩阵R：

在Q里面使用星号(1*)来表示简单已配对，用来区分简单未配对。

3）接着将Q输入到算法中

算法包括两个基本的程序，称为程序I（Routine I ）和程序II（Routine II ）。如图1：

程序I达到关联简单匹配最优后（Ib）进入程序II，程序II达到广义匹配最优后输出(IIb)最优解。

每执行一次Ia会增加一个已配对(即Q中的一个星号*)，每执行一次IIa会减少当前覆盖和（预算总数）。

因为已配对总数的上限是n，而覆盖和的下限是0，保证了这个算法能够终止。

算法步骤总结

1.计算行最大值、列最大值，取较小的作为它的预算，另一个预算全为0，作为初始覆盖；

2.写出关联简单匹配矩阵Q：用1标记配对，用1*标记已配对；

3.求解关联简单最优匹配，获得关键行(活)、关键列(人)；

4.在非关键行、非关键列中计算下降空间的最小值，非关键行减该值，关键列加该值；

5.检查新覆盖是否满足广义最优条件，不满足则回到2，满足则输出最优结果。

5.一个例子

下面的例子演示了算法的程序所涉及到的所有可能（除了程序II的Case 2）：

行最大值的总和 = 9 + 8 + 9 + 6 = 32。

列最大值的总和 = 8 + 7 + 9 + 9 = 33。

32<33，所以初始覆盖(即预算总数)由行最大值32给出。

下面的表格由算法一步步计算得到的覆盖（矩阵外面的数值）

下面解释每一步的覆盖和对应的匹配结果如何构建得来：

第一阶段：

左图：在初始覆盖对应的矩阵中标记1，表示

中图：检查每一行的头一个1，如果未配对则进行配对（标星号）。因为此时关联简单最优，不存在转移，所以不存在关键行（由关键人的定义可知），已匹配的列（3、4）是关键列（由定理1可知，已匹配要不是关键行要不是关键列）。

右图：将关键列和关键行划掉，在图中剩余部分（非关键行、非关键列）中计算 $d=u_i+v_j-r_{ij}$ 的最小值为9+0-8=1，非关键行 $u_1,u_2,u_3,u_4$ 减该值，关键列,加该值。则获得第二个覆盖：

第二阶段：

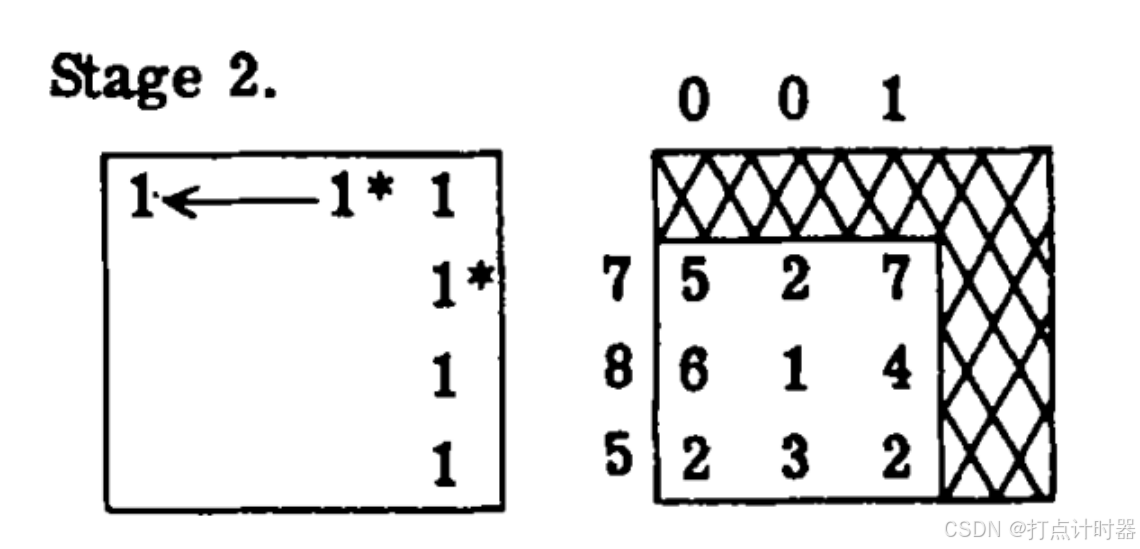
左图：覆盖的改变引入了(1,1)位置的新1。此时关联简单最优，但存在一个转移，用→来表示，所以行1是关键行。因为(2,4)已匹配，且2行是非关键行，所以列4是关键列。

右图：将关键行和关键列划掉，把图中剩余部分（非关键行、非关键列）计算的最小值为7+1-7=1，非关键行、、减该值，关键列加该值。则获得第三个覆盖：

第三阶段：

左图：覆盖的改变引入了(2,3)位置的新1，消除了(1,4)位置的旧1。

中图：这个转移会产生一个不完全匹配结果（因为(3,4)是可配对的，且3行和4列都不存在已配对），把(3,4)进行配对黑猴产生一个完全匹配结果。因为此时关联简单最优，不存在转移，所以不存在关键行，已匹配的列（1、3、4）是关键列。

右图：将关键列和关键行划掉，减少，把图中剩余部分计算的最小值为8+0-7=1，非关键行 $u_1,u_2,u_3,u_4$ 减该值，关键列、、加该值。则获得第四个覆盖：

第四阶段：

左图：覆盖的改变引入了(1,2)和(4,2)位置的新1，此时匹配结果是未完全的，通过配对(4,2)产生完全匹配结果。

右图：检查条件都已满足，此时匹配结果最优（解读：由定理6可得）。

6.证明（选读）

定理1的证明

证明定理1之前先给出几个铺垫：

引理1。给定一个“匹配结果”，在一个配对中，要么这个人是关键人，要么这份工作是关键的，而且不能是两者都是关键的，即两者中有且只有一个是关键的。

推论1。给定一个“匹配结果”，已配对的数量等于关键人和关键活的数量之和。

对引理1和推论1的解释：也就是说，任何一个配对就两种情况，要么可以转移，要么不能转移。配对可以转移的时候，人是关键人，工作是非关键；配对不可转移时，人是非关键人，工作是关键工作。所以显然的就有，配对数=关键人数+关键活数。

        下面的两个引理，用来补充解释关键性（essentiality ）。
        引理2。给定一个“匹配结果”，如果某个人已经配对，并且他有另一项资格胜任的未分配工作，那么这个人就是关键的。
        证明：因为这个人有另一项资格胜任的未配对工作，所以他一定是处于一个转移中，根据定义，他就是关键人。

引理3。给定一个“匹配结果”，如果有一个工作，在所有可能的转移下，它都是（变成或保持）配对的状态，那么这个工作是关键的。
证明。（证逆否命题）假设这份工作j不是关键的，然后需要证明至少存在一个转移使得它变成未配对的。由关键活的定义可以知道非关键活有两种情况，第一种是这个工作j还未配对，这时存在一个保持不变的转移（前面说过，保持不变也算一种转移）使得工作j保持未配对状态，第二种情况是这个工作j已经配对，因为这个工作j是非关键的，所以配对的工人必是关键的，所以必定存在可以将配对到其他工作的一个转移，这个转移使得工作j变成未配对的，这个转移的记号如下，引理3证毕。

定理1。给定一个“匹配结果”，如果所有可能的转移都产生“完全匹配结果”，则这个“匹配结果”是最优的（因为已经无法通过新增匹配或转移进行改进），此时，对于每个可能的（已确定或未确定）配对来说，或者配对人是关键的，或者配对工作是关键的，或者两者都是关键的。

下面开始证明定理1：

假设有个工人i有资格胜任工作j，进行分类讨论。

A.若工人i已配对：

a）如果工人i和工作j配对，由引理1可知，工人i、工作j两者中有一个是关键的。

b）如果工人i配对另一个工作k，并且工作j是未配对的，则由引理2可知，工人i是关键的。

c）如果工人i配对另一个工作k，并且工作j配对工人m，只需证明工人i和工作j不是同时为非关键的。设工作j非关键，则由定义知存在转移使得工作j变成未配对，此时变为b的情况，工人i是关键的，所以工人i和工作j不能同时为非关键的。

B.若工人i未配对：

如果工作j是未配对，工人i和工作j可以进行新的配对，和完全匹配结果相矛盾，所以工作j一定是配对了。接着假设，如果存在某个转移使得工作j未配对（因为转移是已配对的人换其他的工作，转移不影响未配对工人的状态，工人i依然保持未配对），则工人i和工作j可以进行新的配对，这和所有可能的转移都会产生一个完全匹配结果相矛盾，所以所有可能的转移下工作j都只能是配对状态，由引理3可知，工作j是关键的。

定理1证毕。

定理2

从任何一个“匹配结果”开始，要么在转移后得到一个完全匹配结果，要么在转移后至少可以再新增一个配对。因为至多有n个配对（不能无限新增配对），所以可以得到以下结论:

定理2。在执行所有可能的（一次或多次）转移之后可以得到一个完全匹配结果。

定理5

定理5。任意一个“充分预算结果”的预算总数不少于任意一个“匹配结果”的评分总数。

这些不等式相加可得：

整数排列是的一个排列。

定理5得证。

关联简单匹配问题优化步骤的证明

关联简单匹配问题优化步骤的证明如下：

在描述这个步骤之前，注意到一个“充分预算结果”必须给予每个人一个正预算或每个工作一个正预算，否则将存在一些人或工作的预算达不到评分。（解读：反证法，假设有一个工人i的预算为0、且有一个工作j的预算为0，则配对ij的预算为0，显然达不到配对ij的评分要求(正整数)，充分预算结果不成立，矛盾。所以，要不就是每个人都有一个正预算，要不就是每个工作都有一个正预算，或者两者全都是正预算。）

不失一般性地（因为行和列有对称性），我们假定给予每个工人的预算都是正的，

设关联简单已配对的个数是m，m<n。随机给定一个“最优匹配结果”，并令关键人为i=1,...,r，关键活为j=1,...h。由推论1可知：r+h=m。

改进总预算的步骤如下：关键人的预算不变，非关键人的预算减一；关键活的预算加一，非关键活的预算不变

（依然是非负的，因为是正整数。）我们必须检查：

（a）新的“预算结果”是充分的，并且

（b）预算总量下降了。

预算充分性（a）由不等式（1）来检查，对一个广义已配对，只有当下降且保持不变时才会不满足充分性，这意味着工人i和工作j都是非关键的。

由定理1可知（简单已配对中至少有一个是关键的），工人i和工作j是简单未配对的，等号不成立，则有：

因为所有的数值都是正整数，则有：

说明新的“预算结果”也是充分的。(a)成立。

因为总预算下降了n-r 、上升了h，于是总共下降了n - (r+h)= n-m > 0。所以(b)成立。

7.程序设计思路（选读）

程序I

程序I以以下方式与第2节关联：给定一个匹配结果，我们需要列举所有可能的转移。转移是从合适列（没有1和没有1*的列）开始的，所以如果没有合适列，则不存在转移，这个匹配结果是完全的。支路la的发生意味着找到了一个转移，这个转移可以减少一个包含未分配的1的列。在这种情况下，我们执行转移来配对：

如果找到的转移（已经无法继续增加元素），产生了完全匹配结果，则转移的最后一行ik-1被记录为关键行，然后继续枚举转移。如果转移的枚举已完成，没有发生分支la，则进入到分支lb，此时有一个匹配结果，在所有可能的转移下都产生完全匹配结果。

程序I的输入是，一个覆盖的关联矩阵Q，包括在Q上已配对标记（星号*）。

程序I在分支Ib的输出是Q的一个最优匹配结果、以及一系列的关键行。Q中的每个1要不在一个关键行里，要不在关键行1*所在的列里。

程序开始，按顺序搜索矩阵Q的每一列，并试图找到头一个1*。

如果在某一列里找到1*，程序跳到下一列，如果是最后一列，则（走Ib分支）进入程序II。

如果在一列里没有找到一个1*，则这一列被称为合适列(eligible)，然后在这一列搜索1。

（解读：eligible有个意思是合适婚配的，也就是未婚配的意思，因为这个列还没配对后面需要把它配对上，所以叫合适列，搜索1就是在给它找配对者。）

如果没有找到1，则跳到下一列，如果是最后一列，则（走Ib分支）进入程序II。

如果在找到了1（在位置），就开始一个构建序列的子程序，会将、记录下来构建成这样一个序列（解读：该序列用来找可能的转移）：

解读：1可以看做是转移中的箭头，1*看着做是原有的配对。下面我将转移图中的 $i_k$ 称为行元素、 $j_k$ 称为列元素。

下面解释这个序列是如何构建的：

Case1：找到了1（在位置），就在第行搜索1*。

如果在第行没找到1*，则把序列中所有的1改为1*、1*改为1，（进入支路Ia）重新执行程序I。（解读：从1开始，循环找1*和1，到1结束，所以1的个数比1*多一个，反转1和1*的结果就是调整了已匹配和未匹配、使得已匹配总数加一）

Case2：找到了1*（在位置），就在第列中搜索1。

如果没找到1，则第行被记录为关键行（解读：就是找到的这个转移中的最后一个关键人），记录中删除、（最后一个红框），接着从列的行继续搜索1。（解读：思路是从转移的尾部向头部遍历搜索、标记关键人）。

如果（解读：搜索到转移的头部了），则回到合适列列中从行继续搜索1。

如果找到了1（在位置），我们检验 $i_{k+1}$ 是否已在行元素中：

如果 $i_{k+1}$ 还未出现在行元素中，保留 $i_{k+1}$ ，记录、（↙箭头），然后继续在行搜索1*（Case1搜索）。

如果 $i_{k+1}$ 已在行元素中，放弃 $i_{k+1}$ ，回到列从行继续搜索1。

程序I的流程图如图2，有如下记号： tally：计数

程序II

程序II实现了第3节的改进总预算的步骤：关键人的预算不变，非关键人的预算减一；关键活的预算加一，非关键活的预算不变。

程序II的输入是一个覆盖、关键行（关键人）、关键列（关键活）。

如果一个列包含了非关键行1*，这个列称为关键列（也就是关键活的定义：已匹配的人不是关键人）。

首先计算 $d=u_i+v_j-r_{ij}$ ，其中i是非关键行、j是非关键列。

（解读：在第3节中，工人i和工作j都是非关键的才能满足充分性，每次减1的操作需要满足 $u_i+v_j-1 \ge r_{ij}$ ，将多次减1的操作进行合并，使其刚好满足 $u_i+v_j-d=r_{ij}$ ）

如果不存在这样的，则Q中的一系列1*组成了广义匹配问题的解（定理6）。

若d>0，还需要考虑两个互斥的情况：

Case1：对所有非关键行i，。

计算，i为非关键行。然后

对所有非关键行i：，

对所有关键列j：，

（解读：因为要满足充分性，变换后的 $u_i$ 是不能小于0的，所以m只能取 $u_i$ 和d的较小者，超过其中任何一个就不满足充分性了）

Case2：存在一些非关键行i，（解读：前面讲过，行预算里有0则列预算里一定没有0。接着根据行列的对称性，按列来进行预算的下降优化）。

计算，j为非关键列。然后

对所有关键行i： $u_i\rightarrow u_i+m$ ，

对所有非关键列j： $v_j\rightarrow v_j-m$ ，

通过这些操作改变覆盖，进入分支IIa回到程序I。