第四章 二元关系和函数 4.1 集合的笛卡尔与二元关系

4.1 集合的笛卡尔与二元关系

有序对（序偶）

注意：
这里用圆括号和尖括号都可。

我们可以将二元概念推广到$n$元。

接下来，我们进入笛卡尔积的概念：

笛卡尔积中的一些性质：


即：

• 笛卡尔积不适合交换律
• 笛卡尔积不适合结合律
• 笛卡尔积适合分配律
• $A$ X $B$ $=$ $B$ X $A$ 不一定 $B=A$。因为$A$有可能为∅

我们来道证题：

上诉操作方法我们在证明有关积运算的集合恒等式中经常用。
注意$x$与$y$这两个块之间是用$\wedge$连接的。

我们也可以将笛卡尔积推向$n$阶

二元关系：

注意：
二元关系也是一个集合。

二元关系可以是两个集合之间的，也可以是一个集合内部的关系。

大部分关系是没有实际意义的，但是，对于任意集合$A$都有3种特使的关系：

二元关系的个数：

$A$ X $B$的子集每一个都是一个关系。分别是0~n阶，关系逐渐复杂。所以其子集个数也是其关系个数。

例：

我们也可以推广到$n$元关系：

上诉都是以集合的形式来表示关系，我们也可以用关系矩阵和关系图来表示关系，如下：

矩阵表示：

关系图表示：

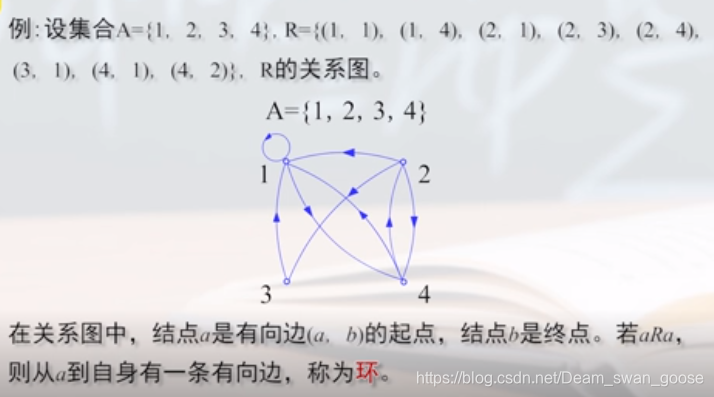
练习：
1.设X为集合，|X|=n，在X上有()种不同的关系？

• $n^2$
• $2^n$
• $2^{2n}$
• $2^{n^2}$ ✔