二元关系和函数

目录

1. 二元关系

1.1 二元关系的概念

2. 关系的运算

2.1 二元关系的域

2.2 逆运算

2.3 复合运算

3. 关系的性质

3.1 性质的定义

4. 关系的闭包

4.1 闭包的定义

5. 等价关系与偏序关系

5.1 等价关系

5.2 划分

5.3 偏序关系

5.4 哈斯图

5.5 特殊元

---

1. 二元关系

1.1 二元关系的概念

（1）设 A、B为两个集合，笛卡儿积为A×B。

（2）设A、B是集合，A×B的任一子集R称为A到B的一个二元关系。

例：设A={a，b}，B={3，4}

A×B = {<a，3>，<a，4>，<b，3>，<b，4>}

（3）恒等关系IA与全域关系EA

例：设A={1，2}

IA = {<1，1>，<1，2>，<2，1>，<2，2>}

EA = {<1，1>，<2，2>}

2. 关系的运算

2.1 二元关系的域

设R是二元关系

（1）R中所有有序对的第一个元素构成的集合，称为R的定义域，记作dom(R)。

（2）R中所有有序对的第二个元素构成的集合，称为R的值域，记作ran(R)。

（3）R的定义域和值域的并集dom(R)∪ran(R)，称为R的域，记作fld(R)。

例：设R={<1，1>，<1，4>，<2，2>，<3，3>}

dom(R) = {1，2，3}，ran(R) = {1，2，3，4}，fld(R) = {1，2，3，4}

2.2 逆运算

（1）称R-1为R的逆关系，即 把所有有序对的第一个元素和第二个元素交换位置。

例：设R={<1，1>，<1，4>，<2，3>，<3，4>}

R-1 = {<1，1>，<4，1>，<3，2>，<4，3>}

2.3 复合运算

（1）设F，G为二元关系，G对F的右复合记作F◦G。一般F◦G不一定等于G◦F。

例：设F={<3，3>，<6，2>}，G={<2，3>}

F◦F = {<3，3>}，G◦G = Æ，F◦G = {<6，3>}，G◦F = {<2，3>}

3. 关系的性质

3.1 性质的定义

假设R为集合A上的关系

（1）自反关系：每个元素都有自调，称R在A上是自反的，在关系图中每个顶点都有环。

（2）反自反关系：不存在任一元素的自调，称R在A上是反自反的，在关系图中每个顶点都没有环。

例：判断下列图形的自反和反自反关系。

图1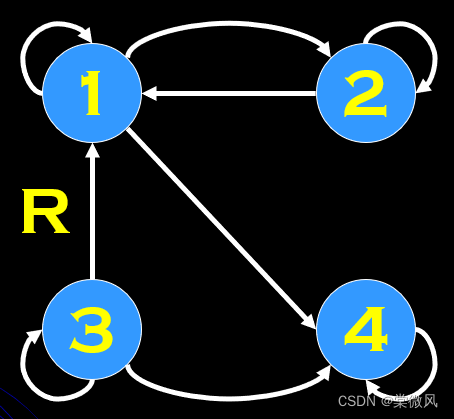 图2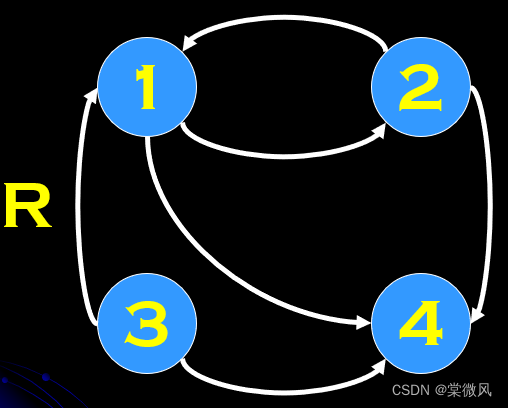

解：图1每个点都有环，所以是自反。

图2每个点都没有环，所以是反自反。

（3）对称关系：在关系图中，两点之间的线都是循环双向的，称为对称关系。

（4）反对称关系：在关系图中，两点之间的线都是单向单线的，称为反对称关系。

如果两点之间的线既有循环双向，又有单向单线，则既不是对称，也不是反对称。

例：判断下列图形的对称和反对称关系。

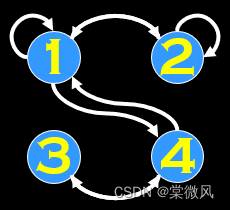图1 图2  图3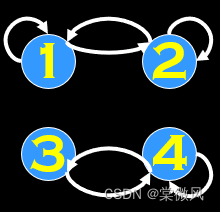

解：图1全是单向单线，所以是反对称。

图2都是循环双向，所以是对称。

图3都是循环双线，所以是对称。

（5）传递关系：在关系图中，如果两点之间有可以间接连通的线，则必须有可以直接连通的线，称为传递关系。注意：只有一个有序对，也是传递关系。

例：判断下列图形的传递关系。

图1 图2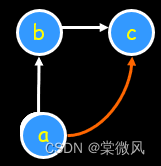

解：图1是传递，图2是传递

（6）关系表

表示	性质
	自反	反自反	对称	反对称	传递
关系图	每个顶点都有环	每个顶点都没有环	全双边	全单边	凡两点能间接到达，则必能直接到达

4. 关系的闭包

4.1 闭包的定义

（1）自反闭包：关系图中每个顶点都有环，记作r(R)。

例：

原图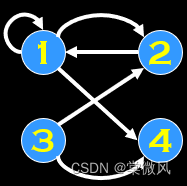：  改为自反闭包：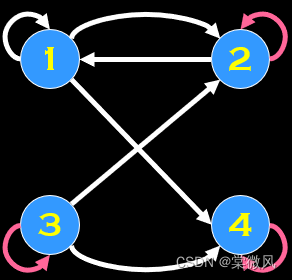

（2）对称闭包：关系图中全是双边，记作s(R)。

例：

原图：  改为对称闭包：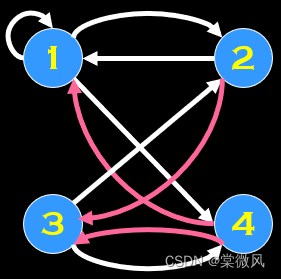

（3）传递闭包：关系图中凡两点能间接到达，则必能直接到达，记作t(R)。如果两点之间是循环双线，则传递闭包中需要给两点加自反环。

例1：

原图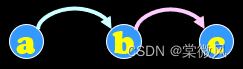：  改为传递闭包：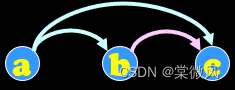

例2：

原图：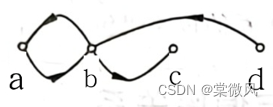

r(R)关系图：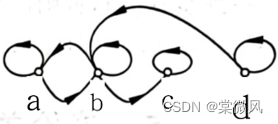

s(R)关系图：

t(R)关系图：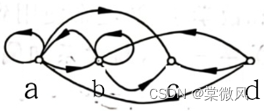

例3：已知R = {<a，b>，<b，a>，<b，c>，<c，d>}，求r(R)，s(R)，t(R)。

r(R)关系图：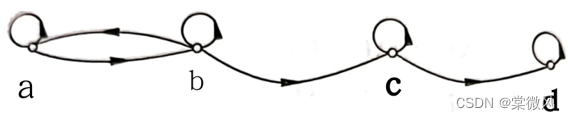

s(R)关系图：

t(R)关系图：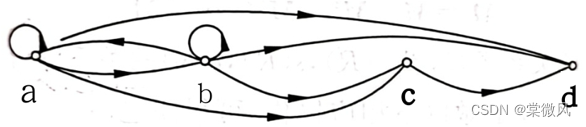

5. 等价关系与偏序关系

5.1 等价关系

如果R是自反、对称和传递的，则称R是A上的等价关系。

5.2 划分

如果集合A的子集族Π满足以下条件：

（1）任意两个子集间没有交集。 （2）所有子集的并集为集合A。

则称Π是A上的一个划分。

例：设A = {1，2，3，4，5}，给定Π1，Π2，Π3，Π4，Π5，判断划分。

Π1 = {{1，2，3}，{3，4，5}}

Π2 = {{1}，{2，3}，{4，5}}

Π3 = {Æ，{1，2，3}，{4，5}}

Π4 = {{1，2，3}，{5}}

Π5 = {{1}，{2}，{3}，{4}，{5}}

解：Π2，Π5是划分，Π1，Π3，Π4不是划分。

Π1有交集3；Π3的空集不是原集合的元素；Π4缺少4。

5.3 偏序关系

如果R是自反、反对称和传递的，则称R是集合A上的偏序关系，记为。集合A和A上的偏序关系一起称作偏序集，记作<A，>。

5.4 哈斯图

偏序关系的关系图就是哈斯图。

例：画出偏序集<{1，2，3，4，5，6，7，8，9，10，11，12，24}，R整除>的哈斯图。

解：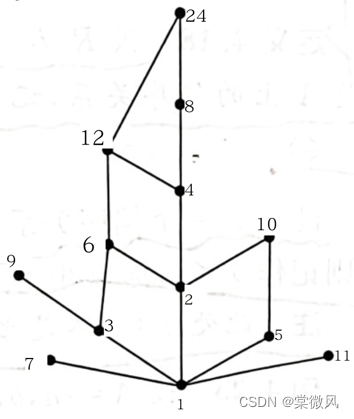

5.5 特殊元

（1）极大元：位于哈斯图的顶层，没有元素可以盖住它。

（2）极小元：位于哈斯图的底层，不能盖住任何元素。

（3）最大元：当极大元只有唯一一个时，那个极大元就是最大元。

（4）最小元：当极小元只有唯一一个时，那个极小元就是最小元。

例：以上题为例，求极大元，极小元，最大元，最小元。

解：极大元为7，9，10，11，24；极小元为1；无最大元；最小元为1。