高等数学笔记-苏德矿
第十章 曲线积分和曲面积分
第四节 第二类曲线积分
第二类曲线积分也称向量值函数的曲线积分。
一、第二类曲线积分的概念
01 解决问题前的基本概念

02 由问题引入积分的定义
问题:求一个质点 M M M 在变力 F ⃗ \vec{F} F (设 F ⃗ \vec{F} F 的分量为连续)作用下,沿着有界**光滑**曲线 Γ A B \Gamma_{AB} ΓAB 由 A A A 点移动到 B B B 点所做的功 W W W 。

分析:微元法的前提:总功等于部分功之和。
由所做的功为 W W W, W W W 分布在曲线 Γ A B \Gamma_{AB} ΓAB 上, ∀ d s ⊂ Γ A B \forall\ ds\subset\Gamma_{AB} ∀ ds⊂ΓAB, d s ds ds 的弧长仍记为 d s ds ds ,在这个弧段上所做的功 Δ W \Delta W ΔW ,求出 Δ W \Delta W ΔW 的等价量 d W dW dW 。
把这个弧上的力看作恒力。 ∀ P ⊂ d s \forall\ P\subset ds ∀ P⊂ds,看成在 P P P 点的力 F ⃗ ( P ) \vec{F}(P) F(P) 。把有向弧看成有向的质线段(向量),大小为 d s ds ds 。
取 P P P 点在切线的单位向量 F 0 ⃗ ( P ) \vec{F^0}(P) F0(P) 。且与指定的方向(由 A A A 到 B B B )一致。
有向弧看成一个向量 d s ⃗ = T 0 ⃗ d s = T 0 ⃗ ( P ) d s d\vec{s}=\vec{T^0}ds=\vec{T^0}(P)ds ds=T0ds=T0(P)ds 。 ( Δ W ≈ ) d W = F ⃗ ( P ) ⋅ T 0 ⃗ ( P ) d s , P ∈ Γ A B (\Delta W\approx)dW=\vec{F}(P)\cdot\vec{T^0}(P)ds\ , \ P\in\Gamma_{AB} (ΔW≈)dW=F(P)⋅T0(P)ds , P∈ΓAB ,
W = ∫ Γ A B F ⃗ ( P ) ⋅ T 0 ⃗ ( P ) d s = ∫ Γ A B [ F ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ] d s = ∫ Γ A B ( F ⃗ ⋅ T 0 ⃗ ) d s W=\int_{\Gamma_{AB}}\vec{F}(P)\cdot\vec{T^0}(P)ds=\int_{\Gamma_{AB}}[\vec{F}(P)\cdot\vec{T^0}(P)]ds=\int_{\Gamma_{AB}}(\vec{F}\cdot\vec{T^0})ds W=∫ΓABF(P)⋅T0(P)ds=∫ΓAB[F(P)⋅T0(P)]ds=∫ΓAB(F⋅T0)ds (特殊的第一类曲线积分)。
称为向量 F ⃗ \vec{F} F 沿着曲线 Γ A B \Gamma_{AB} ΓAB 由 A A A 到 B B B 的第二类曲线积分。
03 给出第二类曲线积分的定义
设向量 A ⃗ ( P ) \vec{A}(P) A(P) 在有界光滑曲线 Γ A B \Gamma_{AB} ΓAB 上有定义,且有界( A ⃗ ( P ) \vec{A}(P) A(P) 的分量是有界函数),
T 0 ⃗ ( P ) \vec{T^0}(P) T0(P) 表示曲线 Γ A B \Gamma_{AB} ΓAB 上点 P P P 处的切线的单位向量且与指定的方向(由 A A A 到 B B B )一致。
若第一类曲线积分 ∫ Γ A B ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s \int_{\Gamma_{AB}}(\vec{A}(P)\cdot\vec{T^0}(P))ds ∫ΓAB(A(P)⋅T0(P))ds 存在,该积分的值称为向量 A ⃗ ( P ) \vec{A}(P) A(P) 沿曲线 Γ A B \Gamma_{AB} ΓAB 由 A A A 到 B B B 的第二类曲线积分,又称向量值函数曲线积分。
二、第二类曲线积分的定理和性质
01 第二类曲线积分的意义
( 物理意义 ) 求一个质点在变力:求一个质点 M M M 在变力 F ⃗ \vec{F} F (设 F ⃗ \vec{F} F 的分量为连续)作用下,
沿着有界光滑曲线 Γ A B \Gamma_{AB} ΓAB 由 A A A 点移动到 B B B 点所做的功 W W W, W = ∫ Γ A B ( F ⃗ ⋅ T 0 ⃗ ) d s W=\int_{\Gamma_{AB}}(\vec{F}\cdot\vec{T^0})ds W=∫ΓAB(F⋅T0)ds 。
02 第二类曲线积分的性质
积分如果把被积函数看成一个整体,它是第一类曲线,此时,具有第一类曲线积分的所有性质。
作为第二类曲线积分具有下面两个独特的性质:
性质1: ∫ Γ A B ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s = − ∫ Γ B A ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s \int_{\Gamma_{AB}}(\vec{A}(P)\cdot\vec{T^0}(P))ds=-\int_{\Gamma_{BA}}(\vec{A}(P)\cdot\vec{T^0}(P))ds ∫ΓAB(A(P)⋅T0(P))ds=−∫ΓBA(A(P)⋅T0(P))ds
与第一类曲线积分不同,第二类曲线积分与曲线方向有关。
性质2: ∫ Γ A B ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s = ∫ Γ A C ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s + ∫ Γ C B ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s \int_{\Gamma_{AB}}(\vec{A}(P)\cdot\vec{T^0}(P))ds=\int_{\Gamma_{AC}}(\vec{A}(P)\cdot\vec{T^0}(P))ds+\int_{\Gamma_{CB}}(\vec{A}(P)\cdot\vec{T^0}(P))ds ∫ΓAB(A(P)⋅T0(P))ds=∫ΓAC(A(P)⋅T0(P))ds+∫ΓCB(A(P)⋅T0(P))ds

注意两点:
(1) 两种曲线积分形式的不同。
(2) Q = 0 或 P = 0 Q=0 \ 或 \ P=0 Q=0 或 P=0, ∫ C P d x 或 ∫ C Q d y \int\limits_{C} P d x \ 或 \ \int \limits_{C} Q d y C∫Pdx 或 C∫Qdy 仍是第二类。
三、第二类曲线积分的分类与计算
分析的准备工作
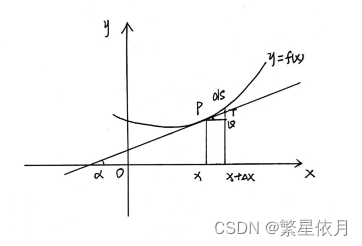
d s ⋅ cos α = ∣ P T ∣ cos α = ∣ P Q ∣ = d x ds\cdot\cos\alpha=|PT|\cos\alpha=|PQ|=dx ds⋅cosα=∣PT∣cosα=∣PQ∣=dx, d s = tan 2 α + 1 ⋅ d x ds=\sqrt{\tan^2\alpha+1}\cdot dx ds=tan2α+1⋅dx
a ⃗ = { x 1 , y 1 , z 1 } \vec{a}=\{x_1,y_1,z_1\} a={x1,y1,z1}, x 1 = a ⃗ ⋅ i ⃗ = ∣ a ⃗ ∣ cos α x_1=\vec{a}\cdot\vec{i}=|\vec{a}|\cos\alpha x1=a⋅i=∣a∣cosα,
y 1 = a ⃗ ⋅ j ⃗ = ∣ a ⃗ ∣ cos β y_1=\vec{a}\cdot\vec{j}=|\vec{a}|\cos\beta y1=a⋅j=∣a∣cosβ, z 1 = a ⃗ ⋅ k ⃗ = ∣ a ⃗ ∣ cos γ z_1=\vec{a}\cdot\vec{k}=|\vec{a}|\cos\gamma z1=a⋅k=∣a∣cosγ
若空间曲线 Γ \Gamma Γ 上点 ( x , y , z ) (x,y,z) (x,y,z) 处,切线的单位向量 T 0 ⃗ = { cos α , cos β , cos γ } \vec{T^0}=\{\cos\alpha,\cos\beta,\cos\gamma\} T0={cosα,cosβ,cosγ} 与指定的方向一致。
T 0 → ⋅ d s = △ d s ⃗ = { cos α , cos β , cos γ } = { d x , d y , d z } \overrightarrow{T_0}\cdot ds\stackrel{\triangle}{=}d\vec{s}=\{\cos\alpha,\cos\beta,\cos\gamma\}=\{dx,dy,dz\} T0⋅ds=△ds={cosα,cosβ,cosγ}={dx,dy,dz}
空间曲线第二类曲线积分的计算
一般形式: ∫ Γ A B ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s = ∫ Γ A B ( A ⃗ ⋅ T 0 ⃗ ) d s \int_{\Gamma_{AB}}(\vec{A}(P)\cdot\vec{T^0}(P))ds=\int_{\Gamma_{AB}}(\vec{A}\cdot\vec{T^0})ds ∫ΓAB(A(P)⋅T0(P))ds=∫ΓAB(A⋅T0)ds
若 Γ A B ⊂ R 3 \Gamma_{AB}\subset\mathrm{R}^3 ΓAB⊂R3, P ( x , y , z ) ∈ Γ A B P(x,y,z)\in\Gamma_{AB} P(x,y,z)∈ΓAB, T ⃗ \vec{T} T 在空间曲线 Γ \Gamma Γ 上点 ( x , y , z ) (x,y,z) (x,y,z) 处,切线的单位向量 T 0 ⃗ \vec{T^0} T0 与指定的方向一致。
T 0 ⃗ = { cos α , cos β , cos γ } \vec{T^0}=\{\cos\alpha,\cos\beta,\cos\gamma\} T0={cosα,cosβ,cosγ} , T 0 → ⋅ d s = △ d s ⃗ = { cos α , cos β , cos γ } = { d x , d y , d z } \overrightarrow{T_0}\cdot ds\stackrel{\triangle}{=}d\vec{s}=\{\cos\alpha,\cos\beta,\cos\gamma\}=\{dx,dy,dz\} T0⋅ds=△ds={cosα,cosβ,cosγ}={dx,dy,dz}
A
⃗
(
x
,
y
,
z
)
=
{
P
(
x
,
y
,
z
)
,
Q
(
x
,
y
,
z
)
,
R
(
x
,
y
,
z
)
}
\vec{A}(x,y,z)=\{P(x,y,z),Q(x,y,z),R(x,y,z)\}
A(x,y,z)={P(x,y,z),Q(x,y,z),R(x,y,z)}
①
∫
Γ
A
B
(
A
⃗
⋅
T
0
⃗
)
d
s
②
=
∫
Γ
A
B
A
⃗
⋅
d
s
⃗
③
=
∫
Γ
A
B
(
P
(
x
,
y
,
z
)
cos
α
+
Q
(
x
,
y
,
z
)
cos
β
+
R
(
x
,
y
,
z
)
cos
γ
)
d
s
=
∫
Γ
A
B
(
P
cos
α
+
Q
cos
β
+
R
cos
γ
)
d
s
④
=
∫
Γ
A
B
[
P
(
x
,
y
,
z
)
d
x
+
Q
(
x
,
y
,
z
)
d
y
+
R
(
x
,
y
,
z
)
d
z
]
=
∫
Γ
A
B
P
d
x
+
Q
d
y
+
R
d
z
(
用
得
较
多
)
⑤
=
∫
Γ
A
B
P
(
x
,
y
,
z
)
d
x
+
∫
Γ
A
B
Q
(
x
,
y
,
z
)
d
y
+
∫
Γ
A
B
R
(
x
,
y
,
z
)
d
z
(
其
实
是
由
第
③
类
一
曲
线
积
分
性
质
得
到
的
,
二
曲
线
积
分
不
能
直
接
用
和
的
积
分
等
于
积
分
的
和
)
\begin{aligned} ①& \ \ \int_{\Gamma_{AB}}(\vec{A}\cdot\vec{T^0})ds\\ ②& \ \ =\int_{\Gamma_{AB}}\vec{A}\cdot d\vec{s}\\ ③& \ \ =\int_{\Gamma_{AB}}(P(x,y,z)\cos\alpha+Q(x,y,z)\cos\beta+R(x,y,z)\cos\gamma)ds\\ & \ \ =\int_{\Gamma_{AB}}(P\cos\alpha+Q\cos\beta+R\cos\gamma)ds\\ ④& \ \ =\int_{\Gamma_{AB}}[P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz]\\ & \ \ =\int_{\Gamma_{AB}}Pdx+Qdy+Rdz\ \ \ (用得较多)\\ ⑤& \ \ =\int_{\Gamma_{AB}}P(x,y,z)dx+\int_{\Gamma_{AB}}Q(x,y,z)dy+\int_{\Gamma_{AB}}R(x,y,z)dz\\ &\quad\quad(其实是由第③类一曲线积分性质得到的,二曲线积分不能直接用和的积分等于积分的和) \end{aligned}
①②③④⑤ ∫ΓAB(A⋅T0)ds =∫ΓABA⋅ds =∫ΓAB(P(x,y,z)cosα+Q(x,y,z)cosβ+R(x,y,z)cosγ)ds =∫ΓAB(Pcosα+Qcosβ+Rcosγ)ds =∫ΓAB[P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz] =∫ΓABPdx+Qdy+Rdz (用得较多) =∫ΓABP(x,y,z)dx+∫ΓABQ(x,y,z)dy+∫ΓABR(x,y,z)dz(其实是由第③类一曲线积分性质得到的,二曲线积分不能直接用和的积分等于积分的和)
如果直接计算二曲线积分,要化成哪一种?
如果直接计算第二类曲线积分,不管给哪一种形式都要化成第④种,把曲线 Γ A B \Gamma_{AB} ΓAB 表示为参数方程:
Γ
A
B
:
{
x
=
x
(
t
)
y
=
y
(
t
)
z
=
z
(
t
)
\Gamma_{AB}:\ \begin{cases}\ x=x(t) \\ \ y=y(t) \\ \ z=z(t)\end{cases}
ΓAB: ⎩⎪⎨⎪⎧ x=x(t) y=y(t) z=z(t) 找出起点
A
A
A 对应的参数
t
A
t_A
tA,找出终点
B
B
B 对应的参数
t
B
t_B
tB 。
∫
Γ
A
B
P
d
x
+
Q
d
y
+
R
d
z
=
∫
t
A
t
B
[
P
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
x
′
(
t
)
+
Q
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
y
′
(
t
)
+
R
(
x
(
t
)
,
y
(
t
)
,
z
(
t
)
)
z
′
(
t
)
]
d
t
\begin{aligned} & \int_{\Gamma_{AB}}Pdx+Qdy+Rdz=\\ & \quad\quad\int_{t_A}^{t_B}[P(x(t),y(t),z(t))x'(t)+Q(x(t),y(t),z(t))y'(t)+R(x(t),y(t),z(t))z'(t)]dt \end{aligned}
∫ΓABPdx+Qdy+Rdz=∫tAtB[P(x(t),y(t),z(t))x′(t)+Q(x(t),y(t),z(t))y′(t)+R(x(t),y(t),z(t))z′(t)]dt
平面曲线第二类曲线积分的计算
一般形式: ∫ Γ A B ( A ⃗ ( P ) ⋅ T 0 ⃗ ( P ) ) d s = ∫ Γ A B ( A ⃗ ⋅ T 0 ⃗ ) d s \int_{\Gamma_{AB}}(\vec{A}(P)\cdot\vec{T^0}(P))ds=\int_{\Gamma_{AB}}(\vec{A}\cdot\vec{T^0})ds ∫ΓAB(A(P)⋅T0(P))ds=∫ΓAB(A⋅T0)ds
若 Γ A B ⊂ R 2 \Gamma_{AB}\subset\mathrm{R}^2 ΓAB⊂R2, P ( x , y ) ∈ Γ A B P(x,y)\in\Gamma_{AB} P(x,y)∈ΓAB, T ⃗ \vec{T} T 在平面曲线 Γ \Gamma Γ 上点 ( x , y ) (x,y) (x,y) 处,切线的单位向量 T 0 ⃗ \vec{T^0} T0 与指定的方向一致。
T 0 ⃗ = { cos α , cos β } \vec{T^0}=\{\cos\alpha,\cos\beta\} T0={cosα,cosβ} , T 0 → ⋅ d s = △ d s ⃗ = { cos α , cos β } = { d x , d y } \overrightarrow{T_0}\cdot ds\stackrel{\triangle}{=}d\vec{s}=\{\cos\alpha,\cos\beta\}=\{dx,dy\} T0⋅ds=△ds={cosα,cosβ}={dx,dy}
A
⃗
(
x
,
y
)
=
{
P
(
x
,
y
)
,
Q
(
x
,
y
)
}
\vec{A}(x,y)=\{P(x,y),Q(x,y)\}
A(x,y)={P(x,y),Q(x,y)}
①
∫
Γ
A
B
(
A
⃗
⋅
T
0
⃗
)
d
s
②
=
∫
Γ
A
B
A
⃗
⋅
d
s
⃗
③
=
∫
Γ
A
B
(
P
(
x
,
y
)
cos
α
+
Q
(
x
,
y
)
cos
β
)
d
s
=
∫
Γ
A
B
(
P
cos
α
+
Q
cos
β
)
d
s
④
=
∫
Γ
A
B
P
(
x
,
y
)
d
x
+
Q
(
x
,
y
)
d
y
=
∫
Γ
A
B
P
d
x
+
Q
d
y
(
用
得
较
多
)
⑤
=
∫
Γ
A
B
P
(
x
,
y
)
d
x
+
∫
Γ
A
B
Q
(
x
,
y
)
d
y
\begin{aligned} ①& \ \ \int_{\Gamma_{AB}}(\vec{A}\cdot\vec{T^0})ds\\ ②& \ \ =\int_{\Gamma_{AB}}\vec{A}\cdot d\vec{s}\\ ③& \ \ =\int_{\Gamma_{AB}}(P(x,y)\cos\alpha+Q(x,y)\cos\beta)ds\\ & \ \ =\int_{\Gamma_{AB}}(P\cos\alpha+Q\cos\beta)ds\\ ④& \ \ =\int_{\Gamma_{AB}}P(x,y)dx+Q(x,y)dy\\ & \ \ =\int_{\Gamma_{AB}}Pdx+Qdy\ \ \ (用得较多)\\ ⑤& \ \ =\int_{\Gamma_{AB}}P(x,y)dx+\int_{\Gamma_{AB}}Q(x,y)dy \end{aligned}
①②③④⑤ ∫ΓAB(A⋅T0)ds =∫ΓABA⋅ds =∫ΓAB(P(x,y)cosα+Q(x,y)cosβ)ds =∫ΓAB(Pcosα+Qcosβ)ds =∫ΓABP(x,y)dx+Q(x,y)dy =∫ΓABPdx+Qdy (用得较多) =∫ΓABP(x,y)dx+∫ΓABQ(x,y)dy
如果直接计算二曲线积分,要化成哪一种?
如果直接计算第二类曲线积分,不管给哪一种形式都要化成第④种,把曲线 Γ A B \Gamma_{AB} ΓAB 表示为参数方程:
Γ
A
B
:
{
x
=
x
(
t
)
y
=
y
(
t
)
\Gamma_{AB}:\ \begin{cases}\ x=x(t) \\ \ y=y(t) \end{cases}
ΓAB: { x=x(t) y=y(t) 找出起点
A
A
A 对应的参数
t
A
t_A
tA,找出终点
B
B
B 对应的参数
t
B
t_B
tB 。
∫
Γ
A
B
P
d
x
+
Q
d
y
=
∫
t
A
t
B
[
P
(
x
(
t
)
,
y
(
t
)
)
x
′
(
t
)
+
Q
(
x
(
t
)
,
y
(
t
)
)
y
′
(
t
)
]
d
t
\begin{aligned} & \int_{\Gamma_{AB}}Pdx+Qdy=\int_{t_A}^{t_B}[P(x(t),y(t))x'(t)+Q(x(t),y(t))y'(t)]dt \end{aligned}
∫ΓABPdx+Qdy=∫tAtB[P(x(t),y(t))x′(t)+Q(x(t),y(t))y′(t)]dt
对于平面曲线
Γ
A
B
\Gamma_{AB}
ΓAB,在五种“平二曲线积分“的基础上,曲线的方程又有以下几种情况。
① Γ A B : y = φ ( x ) , x ∈ [ a , b ] \Gamma_{AB}:y=\varphi(x),x\in[a,b] ΓAB:y=φ(x),x∈[a,b],( x = x x=x x=x ) 特殊的参数方程
② Γ A B : y = a ( 常 数 ) \Gamma_{AB}:y=a\ (常数) ΓAB:y=a (常数), ( x = x x=x x=x ) 特殊的参数方程
③ Γ A B : x = ψ ( y ) , y ∈ [ c , d ] , ψ ’ ( x ) \Gamma_{AB}:x=\psi(y)\ , \ y\in[c,d]\ , \ \psi’(x) ΓAB:x=ψ(y) , y∈[c,d] , ψ’(x) 连续 ( y = y y=y y=y ) 特殊的参数方程
④ Γ A B : x = a ( 常 数 ) , y ∈ [ c , d ] , ψ ’ ( x ) \Gamma_{AB}:x=a\ (常数)\ , \ y\in[c,d]\ , \ \psi’(x) ΓAB:x=a (常数) , y∈[c,d] , ψ’(x) 连续 ( y = y y=y y=y ) 特殊的参数方程
⑤ Γ A B : r = r ( θ ) , θ ∈ [ α , β ] , r ′ ( θ ) \Gamma_{AB}:r=r(\theta)\ , \ \theta\in[\alpha,\beta]\ , \ r'(\theta) ΓAB:r=r(θ) , θ∈[α,β] , r′(θ) 连续
⇒ { x = r ( θ ) cos θ y = r ( θ ) sin θ θ ∈ [ α , β ] \Rightarrow\ \begin{cases}\ x=r(\theta)\cos\theta \\ \ y=r(\theta)\sin\theta\end{cases}\quad\theta\in[\alpha,\beta] ⇒ { x=r(θ)cosθ y=r(θ)sinθθ∈[α,β] , x ′ 2 ( θ ) + y ′ 2 ( θ ) = r 2 ( θ ) + r ′ 2 ( θ ) x'^2(\theta)+y'^2(\theta)=r^2(\theta)+r'^2(\theta) x′2(θ)+y′2(θ)=r2(θ)+r′2(θ)
⑥ Γ A B : θ = θ ( r ) , r ∈ [ a , b ] , θ ′ ( r ) \Gamma_{AB}:\theta=\theta(r)\ , \ r\in[a,b]\ , \ \theta'(r) ΓAB:θ=θ(r) , r∈[a,b] , θ′(r) 连续
⇒ { x = r cos θ ( r ) y = r sin θ ( r ) r ∈ [ a , b ] \Rightarrow\ \begin{cases}\ x=r\cos\theta(r) \\ \ y=r\sin\theta(r)\end{cases}\quad r\in[a,b] ⇒ { x=rcosθ(r) y=rsinθ(r)r∈[a,b]
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








