FAN: Fourier Analysis Networks 翻译

Doc2X：科研翻译与解析工具
提供 批量PDF处理、公式解析、多栏识别，以及 GPT 翻译 与 深度语料提取功能。
Doc2X: Research Translation and Parsing Tool
Offers batch PDF processing, formula parsing, multi-column recognition, along with GPT translation and corpus extraction.
👉 立即使用 Doc2X | Use Doc2X Now

原文链接：https://arxiv.org/pdf/2410.02675

FAN: Fourier Analysis Networks

FAN: 傅里叶分析网络

Yihong Dong ${}^{1\ast }$ ,Ge Li ${}^{1\ast }$ ,Yongding Tao ${}^1$ ,Xue Jiang ${}^1$ ,Kechi Zhang ${}^1$ ,Jia Li ${}^{-1}$ , Jing ${\mathrm{Su}}^2$ ,Jun Zhang ${}^2$ ,Jingjing Xu ${}^2$

Yihong Dong ${}^{1\ast }$ ,Ge Li ${}^{1\ast }$ ,Yongding Tao ${}^1$ ,Xue Jiang ${}^1$ ,Kechi Zhang ${}^1$ ,Jia Li ${}^{-1}$ , Jing ${\mathrm{Su}}^2$ ,Jun Zhang ${}^2$ ,Jingjing Xu ${}^2$

${}^1$ School of Computer Science,Peking University ${}^2$ ByteDance

${}^1$ 北京大学计算机科学学院 ${}^2$ 字节跳动

dongyh@stu.pku.edu.cn, lige@pku.edu.cn

dongyh@stu.pku.edu.cn, lige@pku.edu.cn

Abstract

摘要

Despite the remarkable success achieved by neural networks, particularly those represented by MLP and Transformer, we reveal that they exhibit potential flaws in the modeling and reasoning of periodicity, i.e., they tend to memorize the periodic data rather than genuinely understanding the underlying principles of periodicity. However, periodicity is a crucial trait in various forms of reasoning and generalization, underpinning predictability across natural and engineered systems through recurring patterns in observations. In this paper, we propose FAN, a novel network architecture based on Fourier Analysis, which empowers the ability to efficiently model and reason about periodic phenomena. By introducing Fourier Series, the periodicity is naturally integrated into the structure and computational processes of the neural network, thus achieving a more accurate expression and prediction of periodic patterns. As a promising substitute to multi-layer perceptron (MLP), FAN can seamlessly replace MLP in various models with fewer parameters and FLOPs. Through extensive experiments, we demonstrate the effectiveness of FAN in modeling and reasoning about periodic functions, and the superiority and generalizability of FAN across a range of real-world tasks, including symbolic formula representation, time series forecasting, and language modeling.

尽管神经网络，特别是多层感知器（MLP）和变换器（Transformer），取得了显著成功，但我们揭示它们在周期性建模和推理方面存在潜在缺陷，即它们倾向于记忆周期性数据，而不是对周期性的基本原理进行真正理解。然而，周期性是各种推理和泛化形式中的一个关键特征，通过观察中的重复模式支撑着自然和工程系统的可预测性。在本文中，我们提出了FAN，一种基于傅里叶分析的新型网络架构，它增强了有效建模和推理周期现象的能力。通过引入傅里叶级数，周期性自然地融入了神经网络的结构和计算过程，从而实现了对周期模式的更准确表达和预测。作为多层感知器（MLP）的有前景替代品，FAN可以在各种模型中无缝替代MLP，并且参数和FLOPs更少。通过广泛的实验，我们证明了FAN在建模和推理周期函数方面的有效性，以及FAN在包括符号公式表示、时间序列预测和语言建模等一系列现实任务中的优越性和泛化能力。

1 Introduction

1 引言

The flourishing of modern machine learning and artificial intelligence is inextricably linked to the revolutionary advancements in the foundational architecture of neural networks. For instance, multilayer perceptron (MLP) (Rosenblatt, 1958, Haykin, 1998) plays a pivotal role in laying the groundwork for current deep learning models, with its expressive power guaranteed by the universal approximation theorem (Hornik et al. 1989). Recent claims about the impressive performance of large models on various tasks are typically supported by Transformer architecture (Vaswani et al. 2017; Touvron et al. 2023, OpenAI, 2023). In this context, the community’s enthusiasm for research on neural networks has never diminished. Some emerged neural networks demonstrate notable capabilities in specific fields (Gu & Dao, 2023; Liu et al., 2024), sparking widespread discussion within the community.

现代机器学习和人工智能的蓬勃发展与神经网络基础架构的革命性进展密不可分。例如，多层感知器（MLP）（Rosenblatt, 1958; Haykin, 1998）在当前深度学习模型的基础奠定中发挥了关键作用，其表达能力得到了通用逼近定理（Hornik et al. 1989）的保证。关于大型模型在各种任务上表现出色的最新说法通常得到了Transformer架构（Vaswani et al. 2017; Touvron et al. 2023, OpenAI, 2023）的支持。在这种背景下，社区对神经网络研究的热情从未减退。一些新兴的神经网络在特定领域表现出显著能力（Gu & Dao, 2023; Liu et al., 2024），引发了社区内的广泛讨论。

Beneath the surface of apparent prosperity, we uncover a critical issue that remains in existing neural networks: they struggle to model the periodicity from data. We showcase this issue through an empirical study as illustrated in Figure 1. The results indicate that existing neural networks, including MLP (Rosenblatt, 1958), KAN (Liu et al., 2024), and Transformer (Vaswani et al., 2017), face difficulties in fitting periodic functions, even on a simple sine function. Although they demonstrate

在表面繁荣之下，我们揭示了现有神经网络中存在的一个关键问题：它们难以从数据中建模周期性。我们通过实证研究展示了这一问题，如图1所示。结果表明，现有的神经网络，包括MLP（Rosenblatt, 1958）、KAN（Liu et al., 2024）和Transformer（Vaswani et al., 2017），在拟合周期函数时面临困难，即使是在简单的正弦函数上。

---

*Equal Contribution

*同等贡献

${}^{†}$ This work was supported by a cooperation project between Peking University and ByteDance Company. During this time, Yihong was also an intern at ByteDance.

${}^{†}$ 本研究得到了北京大学与字节跳动公司合作项目的支持。在此期间，Yihong 也在字节跳动实习。

${}^{‡}$ The code is available at https://github.com/YihongDong/FAN

${}^{‡}$ 代码可在 https://github.com/YihongDong/FAN 获取

---

Figure 1: The performance of different neural networks within and outside the domain of their training data for the sine function,where $x$ is a scalar variable.

图1：不同神经网络在其训练数据域内外对正弦函数的性能，其中 $x$ 是一个标量变量。

proficiency in interpolation within the domain of training data, they tend to falter when faced with extrapolation challenges of test data, especially in the out-of-domain (OOD) scenarios. Therefore, their generalization capacity is primarily dictated by the scale and diversity of the training data, rather than by the learned principles of periodicity to perform reasoning. We argue that periodicity is an essential characteristic in various forms of reasoning and generalization, as it provides a basis for predictability in many natural and engineered systems by leveraging recurring patterns in observations.

在训练数据领域内的插值能力方面，它们在面对测试数据的外推挑战时往往会出现问题，尤其是在域外（OOD）场景中。因此，它们的泛化能力主要受到训练数据的规模和多样性的影响，而不是通过学习的周期性原则来进行推理。我们认为，周期性是各种推理和泛化形式中的一个重要特征，因为它通过利用观察中的重复模式，为许多自然和工程系统提供了可预测性的基础。

In this paper, we investigate a key research problem: How to enable neural networks to model periodicity? One core reason existing neural networks fail to model periodicity is that they heavily rely on data-driven optimization without explicit mechanisms to understand the underlying principles in the data. To this end, we propose a Fourier Analysis Network (FAN), a novel neural network framework based on Fourier Analysis. By leveraging the power of Fourier Series, we explicitly encode periodic patterns within the neural network, offering a way to model the general principles from the data. FAN holds great potential as a substitute to traditional MLP, which not only exhibits exceptional capabilities in periodicity modeling but also demonstrates competitive or superior effects on general tasks.

在本文中，我们研究一个关键的研究问题：如何使神经网络能够建模周期性？现有神经网络未能建模周期性的一个核心原因是它们在很大程度上依赖于数据驱动的优化，而没有明确的机制来理解数据中的基本原则。为此，我们提出了一种傅里叶分析网络（FAN），这是一种基于傅里叶分析的新型神经网络框架。通过利用傅里叶级数的力量，我们在神经网络中明确编码周期性模式，为从数据中建模一般原则提供了一种方法。FAN作为传统多层感知器（MLP）的替代品具有巨大的潜力，不仅在周期性建模方面表现出色，而且在一般任务上也展现出竞争力或更优的效果。

To verify the effectiveness of FAN, we conduct extensive experiments from two main aspects: periodicity modeling and application of real-world tasks. 1) For periodicity modeling, FAN achieves significant improvements in fitting both basic and complex periodic functions, compared to existing neural networks (including MLP, KAN, and Transformer), particularly in OOD scenarios. 2) FAN demonstrates superior performance in real-world tasks, including symbolic formula representation, time series forecasting, and language modeling. The experimental results indicate that FAN outperform baselines (including MLP, KAN, and Transformer) for symbolic formula representation task, and Transformer with FAN surpasses the competing models (including Transformer, LSTM (Hochreiter & Schmidhuber, 1997), and Mamba (Gu & Dao, 2023)), for time series forecasting and language modeling tasks. As a promising substitute to MLP, FAN improves the model’s generalization performance meanwhile reducing the number of parameters and floating point of operations (FLOPs) employed. We believe FAN is promising to be an important part of the fundamental model backbone.

为了验证 FAN 的有效性，我们从两个主要方面进行广泛实验：周期性建模和现实世界任务的应用。1) 在周期性建模方面，与现有的神经网络（包括 MLP、KAN 和 Transformer）相比，FAN 在拟合基本和复杂周期函数方面取得了显著改善，特别是在 OOD 场景中。2) FAN 在现实世界任务中表现出色，包括符号公式表示、时间序列预测和语言建模。实验结果表明，FAN 在符号公式表示任务中优于基线（包括 MLP、KAN 和 Transformer），而结合 FAN 的 Transformer 在时间序列预测和语言建模任务中超越了竞争模型（包括 Transformer、LSTM（Hochreiter & Schmidhuber, 1997）和 Mamba（Gu & Dao, 2023））。作为 MLP 的一种有前景的替代方案，FAN 在提高模型的泛化性能的同时减少了所需的参数数量和浮点运算（FLOPs）。我们相信 FAN 有望成为基础模型骨干的重要组成部分。

2 Preliminary Knowledge

2 初步知识

Fourier Analysis (Stein & Weiss, 1971; Duoandikoetxea, 2024) is a mathematical framework that decomposes functions into their constituent frequencies, revealing the underlying periodic structures within complex functions. At the heart of this analysis lies Fourier Series (Tolstov, 2012), which expresses a periodic function as an infinite sum of sine and cosine terms. Mathematically, for a function $f\left(x\right)$ ,its Fourier Series expansion can be represented as:

傅里叶分析（Stein & Weiss, 1971；Duoandikoetxea, 2024）是一个数学框架，将函数分解为其组成频率，揭示复杂函数中的潜在周期结构。这一分析的核心是傅里叶级数（Tolstov, 2012），它将一个周期函数表示为正弦和余弦项的无限和。从数学上讲，对于一个函数 $f\left(x\right)$ ，其傅里叶级数展开可以表示为：

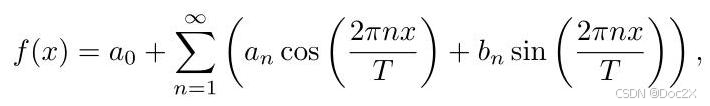
where $T$ is the period of the function,and the coefficients $a_n$ and $b_n$ are determined by integrating the function over one period:

其中 $T$ 是函数的周期，而系数 $a_n$ 和 $b_n$ 通过在一个周期内对函数进行积分来确定：

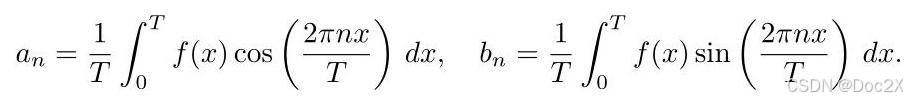
The power of Fourier Series lies in its ability to represent a wide variety of functions, including nonperiodic functions through periodic extensions, enabling the extraction of frequency components. Building on this mathematical foundation, FAN aims to embed the periodic characteristics directly into network architecture, enhancing generalization capabilities and performance on various tasks, particularly in scenarios requiring the identification of patterns and regularities.

傅里叶级数的力量在于它能够表示各种函数，包括通过周期扩展表示的非周期函数，从而提取频率成分。在此数学基础上，傅里叶分析网络（FAN）旨在将周期特性直接嵌入网络架构中，增强在各种任务上的泛化能力和性能，特别是在需要识别模式和规律的场景中。

3 Fourier Analysis Network (FAN)

3 傅里叶分析网络（FAN）

In this section, we first construct a simple neural network modeled by the formula of Fourier Series, and then on this basis, we design FAN and provide its details. Finally, we discuss the difference between the FAN layer and the MLP layer.

在本节中，我们首先构建一个简单的神经网络，该网络以傅里叶级数的公式为模型，然后在此基础上设计FAN并提供其详细信息。最后，我们讨论FAN层与MLP层之间的区别。

Consider a task involving input-output pairs { x i , y i } \left\{ { {x}_{i},{y}_{i}}\right\} { xi​,yi​} ,with the objective of identifying a function $f\left(x\right):{\mathbb{R}}^{d_x}\to {\mathbb{R}}^{}$