离散数学2

集合

1.集合的表示

整数集合Z 正整数集合N

列元素法

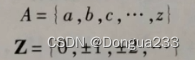
谓词表示法

集合的元素都是集合

集合的元素是无序的

集合的元素与集合之间是属于关系

任何集合A都有 A不属于A

2.集合间关系

A B为两个集合 其中B中每个元素都是A中的元素 则B是A的子集，称B被A包含 也称A包含B

A B相等，即 记作A=B

B属于但不等于A 则为真子集

空集里面无元素

空集是一切集合的子集  空集是唯一的

幂集

含有n个元素的集合简称n元集 它的含有m(m≤n)个元素的子集叫m元子集

0元子集为空集 一元子集也叫单元集

定义：A为集合，把A的全部子集构成的集合叫A的幂集 记作P(A) 或 

在一个具体的问题中，如果所涉及的集合都是某个集合的子集，则称此集合为全集 全集具有相对性 同一个问题也可以有不同的全集

3.集合的运算

基本运算有并 交 对补 对称差

A-B为B对A的相对补集          若两个集合交集为空集 则这两个集合不相交

对称差：A⊕B=B⊕A=（A-B）∪（B-A）

A⊕B=（A∪B）-（A∩B）

注意：A⊕A≠A

给定全集E以后，A包含于E，A的绝对补集~A

~A=E-A={x|x∈E∩x∉A}

广义并：A为集合，A的元素的元素构成的集合为A的广义并 记作∪A

广义交：A为非空集合，A的所有元素的公共元素构成的集合 记作∩A

空集只有广义并没有广义交

一类运算：广义并 广义交 幂集 绝对补运算

二类运算：并 交 相对补 对称差

一类运算优先 一类运算从右向左算 二类运算由括号决定先后顺序

A={{a}，{a,b}}

画图解决

4.集合恒等式

幂等律 A∩A=A，A∪A=A

结合律 (A∩B)∩C=A∩(B∩C)

交换律 A∪B=B∪A

分配律 A∪(B∩C)=(A∪B)∩(A∪C)           A∩(B∪C)=(A∩B)∪(A∩C)

同一律 A∪Ø=A  A∩E=A

零律 A∪E=E A∩Ø=Ø

排中律 A∪~A=E

矛盾律 A∩~A=Ø

吸收律 A∪(A∩B)=A      A∩(A∪B)=A

德摩根律 A-(B∪C)=(A-B)∩(A-C)          ~(B∪C)=~B∩~C        ~Ø=E      ~E=Ø

双重否定律 ~(~A)=A

常用证明技巧：

A-B⊆A    A-B=A∩~B（把相对补转成交运算）      ∩~ = -

(A-B)∪B=A∪B

二元关系

1.有序对和笛卡尔积

有序对：两个元素x,y（x可以=y）按一定顺序排列成的二元组叫做有序对或序偶 记作<x,y> x为第一元素，y为第二元素

有序对的元素是有序的，集合中的元素是无序的

性质：x≠y时，<x,y>不等于<y,x>

<x,y>=<u,v>充分必要条件x=u,y=v

笛卡尔积：A，B为集合，用A中元素为第一元素，B中元素为第二元素构成有序对，所有这样的有序对组成的集合叫作A和B的笛卡尔积 记作A×B  符号化

性质：A×Ø=Ø  Ø×A=Ø

一般不满足交换律和结合律

对并和交满足分配律：

A×(B∪C)=(A×B)∪(A×C)

A×(B∩C)=(A×B)∩(A×C)

A⊆C ∧ B⊆D ⇒ A×B⊆C×D

2.二元关系

若一个集合满足以下条件之一：

 集合非空，它的元素都是有序对

 集合是空集

则称该集合为一个二元关系 记作R      <x,y>∈R 记作xRy

设A，B为集合，A×B的任何子集所定义的二元关系称作从A到B的二元关系，特别当A=B时称作A上的二元关系

如A={0，1} B={1，2，3}

R1={<0,2>}   R2=A×B  R3=Ø，R4={<0,1>}等都是从A到B的二元关系，R3与R4同时也是A上的二元关系

先找A×B={<0,1>,<0,2>,<0,3>,<1,1>,<1,2>,<1,3>}

对任何集合A，空集Ø是A×A的子集 叫A上的空关系

全域关系E 恒等关系I

例如A={1,2}      EA={<1,1>,<1,2>,<2,1>,<2,2>}    IA={<1,1>,<2,2>}

3.关系表示法

关系矩阵

关系图

4.关系运算

1.定义域、值域、域、逆关系

   设R是二元关系

R中所有的有序对的第一元素构成的集合称为R的定义域 记作domR

R中所有的有序对的第二元素构成的集合称为R的值域  记作ranR

R的域记作fldR    fldR = domR∪ranR

R的逆关系 记作={<x,y>|<y,x>∈R}

例：R={<1,2>,<1,3>,<2,4>,<4,3>}

domR={1,2,4}     ranR={2,3,4}   fldR={1,2,3,4}  ={<2,1>,<3,1>,<4,2>,<3,4>}

例：F={<3,3>,<6,2>},G={<2,3>} FoG={<6,3>}

2.限制、象、关系运算的优先顺序

例：R={<1,2>,<1,3>,<2,2>,<2,4>,<3,2>}

R↾{1}={<1,2>,<1,3>}

R↾Ø=Ø

R↾{2,3}={<2,2>,<2,4>,<3,2>}

R[{1}]={2,3}    R[Ø]=Ø    R[{3}]={2}

关系运算优先于集合运算 逆运算优先于其它运算

3.运算的性质

=

dom=ran     ran=dom

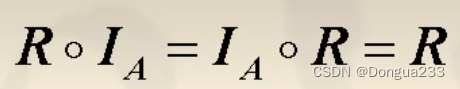
与限制一样

4.关系的幂

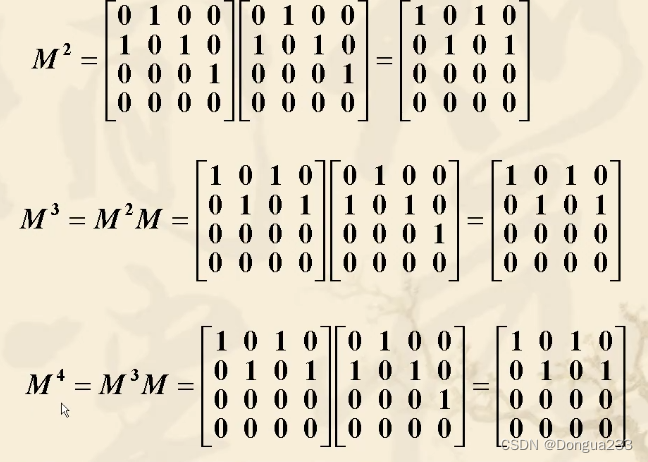
5.关系的性质

自反性、反自反性、对称性、反对称性、传递性

图论

1.定义

图是一个三元组<V(G),E(G),pG>,其中V(G)是一个非空的结点集合,E(G)是边集合，pG是从边集合E到结点无序偶(有序偶)集合上的函数。

若|V(G)|=n，则称G为n阶图。

若|V(G)|与|E(G)|均为有限数，则称G为有限图。

若边集E(G)=0，则称G为零图，此时，又若G为1阶图，则称为平凡图(只含有一个顶点的图)。

一个顶点不与任何边相连 则为孤立点

始终点为一个 则为环

连接着同一个顶点的很多边 称为平行边

含平行边为多重图

无环无平行边为简单图

2.点的度数

点相关边的个数为度 记作deg(v)

 在有向图中 顶点被指向的叫入度 记作d-(v) 指出去的叫出度 记作d+(v)

度数=出度+入度

最大(出、入)度 最小度

最大：Δ  最小：δ

度数为1的顶点叫悬挂点 与该顶点有关的边叫悬挂边

偶度顶点 奇度顶点

3.握手定理

1.无向图中

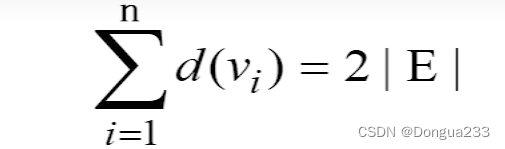
各顶点度数和等于边数的二倍 2m=2|E| 每条边包括环都有两个端点 即提供两度(2m)

G为任意n阶无向简单图 则(G)≤n-1

2.有向图中

出度=入度=|E|

各顶点度数和等于边数的二倍

推论：任意图中，奇度顶点有偶数个

4.完全图

每对结点都有边相连 有n个结点的无向完全图记作Kn

在Kn中对每条边任意确定一个方向 成为有向完全图

n个结点的无向完全图边的数量为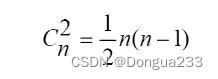

5.子图和补图

补图：使一个图成为完全图的图 边少了

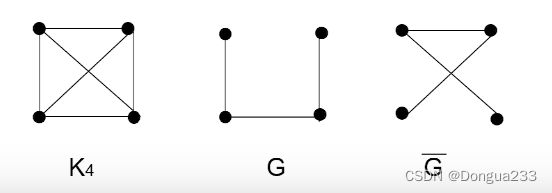
子图：点集和边集都是一个集的子集 点和边都少了

生成子图：点没有少

拿掉点 边可能会变化

6.图的同构（等价关系）

结点和边分别存在一一对应并保持关联关系(充要条件)

同构的必要条件：结点数相同 边数相等 度数相同的结点数相等

一个自互补图顶点数目为4k或4k+1个 k为正整数

7.路与回路

交替序列v0e1v1e2......envn称为联结v0到vn的路 v0：起点 vn：终点 n：路的长度

当v0=vn时，为回路 

若路中所有的边均不相同 称为迹

若路中所有结点均不相同 称为通路

若除v0=vn外 所有结点均不同 称为圈

n阶图中 如果vj到vk存在一条路 则一定存在一条不多于n-1条边的路

推论：.....必存在一条不多于n-1条边的通路

8.连通图与连通分支

无向图中 两结点之间存在一条路 称两结点连通

自反，对称，传递

连通图：在无向图或平凡图中，任意两点都是连通的

把无向图中相互连通的点构成的子图称为连通分支

连通分支数W(G)

图的连通程度：

W(G)=1 为连通图、完全图   W(G)>1 非连通图

W(G)=n 零图

G1为连通图 W(G)=1       G2为非连通图 W(G)=4

9.割集、连通度

无向图G=<V,E>中，只有把V1全部删掉后才不连通，少删任一V1包含的顶点后原图都连通。称V1是G的一个点割集。

边割集同理 割边也叫桥

割点的充要条件：存在两个结点u、w，使得结点u和w的每条路都通过v

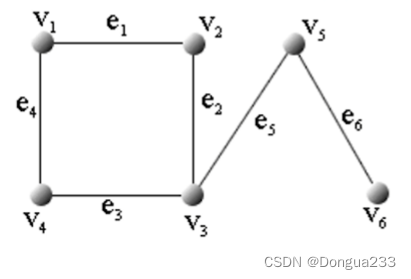
删除V1 V2 V4其中的一个 仍连通 不是点割集  {v2，v4} {v3} {v5}都是点割集，v3、v5都是割点

注意：v1和v3不能构成点割集

无向连通图中，

为G的点连通度

连通度：产生一个不连通图需要删去点的最少数目

边连通度

注：非连通图的点(边)连通度为0 完全图Kn的点(边)连通度为n-1

存在割点(边)的连通图点(边)连通度为1

无向图G：k(G)≤λ(G)≤δ(G)

10.有向图连通

有向图D=<V，E>中结点u到v有一条路，称从u可达v。

u到v的路中最短的一条叫距离

任何一对结点之间至少由一个结点到另一个结点是可达的 为单向连通  相互可达 为强连通 

若略去边方向看成无向图后，图连通，为弱连通

强连通与单向连通的判定定理

D是强连通当且仅当D中存在经过每个顶点至少一次的回路

D是单向连通图当且仅当D中存在经过每个顶点至少一次的通路

11.图的矩阵表示

邻接矩阵

设G<V,E>是一个简单图，它有n个结点，n阶方阵A(G)=(aij)称为G的邻接矩阵

可达矩阵

关联矩阵

12.欧拉图

给定无孤立点的图G，若存在一条路，经过所有边一次且仅一次，称为欧拉路；若存在经过图中所有边一次且仅一次的回路称为欧拉回路

• 具有欧拉回路的图为欧拉图
• 有欧拉路无欧拉回路的图为半欧拉图

给定有向图D，通过图中每边一次且仅一次的一条单向路(回路)，称作单向欧拉路(欧拉回路)

• 无孤立点的无向图G具有一条欧拉路 当且仅当 G是连通的且有0或2个奇度结点
• 有向图G具有一条单向欧拉路，当且仅当它连通，且除两个顶点外，每个结点的出入度相等，这两个结点中，一个结点的入度比出度大1，另一个小1
• 有向图G具有一条单向欧拉回路，当且仅当它是连通的，且每个结点入度等于出度

两个以上奇度顶点 图不能一笔画出

13.哈密顿图

给定无孤立点的图G，若存在一条路，经过所有结点一次且仅一次，称为哈密顿路；若存在经过图中所有边一次且仅一次的回路称为哈密顿回路

• 具有哈密顿回路的图为哈密顿图
• 有哈密顿路无哈密顿回路的图为半哈密顿图

、

若G中有割点或桥，则G不是哈密顿图

判定

VjVi为任意不相邻顶点