ACM教程 - 自适应辛普森积分

陆克和他的那些代码

已于 2022-06-04 10:18:49 修改

阅读量2k

点赞数 1

分类专栏： # ACM 文章标签： ACM 数论自适应辛普森积分

于 2018-08-09 11:35:37 首次发布

本文链接：https://blog.csdn.net/Dream_Weave/article/details/81533415

版权

ACM 专栏收录该内容

47 篇文章

订阅专栏

一、概念

辛普森积分是数值积分的一种，是中点公式和梯形公式的改进。

二、解析

假定我们要求如下定积分：

$\int_a^bf(x)dx$ $∫baf(x)dx∫abf(x)dx$

略微懂一点微积分知识的都知道，对于一个黎曼可积的函数，我们要求其在某个闭区间上的定积分，要先求该函数的不定积分，即先求原函数。就是找到一个函数 F(x)，使得 F′(x)=f(x)，然后根据牛顿—莱布尼茨公式去搞。即：

$\int_a^bf(x)dx=F(b)-F(a)$

而有时候原函数并不好求，比如要求原的函数长得很复杂，要求的原函数非初等函数。这时我们需要“避其锋芒”，采用一种利用“近似”思想的方法。

我们都知道定积分就是曲线 f(x) 下方的面积(假设 f(x) 恒大于 0 )，我们考虑一种近似求出曲线下方面积的方法——辛普森法。

我们先在区间[a,b]中等距地取奇数个点a=x0,x1,x2,...,xn=b，相邻两点间的距离为Δx，再设yi=f(xi)，然后套用公式：

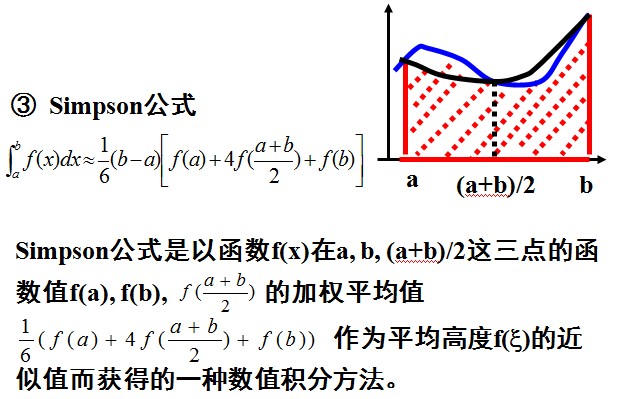
$\small \int_a^bf(x)dx \approx{\Delta x\over3}(y_0+4y_1+y_2)+{\Delta x\over3}(y_2+4y_3+y_4)+...+{\Delta x\over3}(y_{n-2}+4y_{n-1}+y_n)$

点取得越多，近似程度就越高，但计算量也越大。当只取三个点的时候，有：

$\small \int_a^bf(x)dx\approx{ b-a\over6}[f(a)+4f({a+b\over2})+f(b)]$

这就是三点辛普森公式，又简称辛普森公式。

然而如果只取三个点误差肯定大，取太多的点计算量也会上去。那么到底取多少个点合适呢？

还好辛普森积分有一个重要的“变种”，称为自适应辛普森法(adaptive Simpson’s rule)，我们设置一个精度Eps，让算法根据具体情况递归的划分区间，容易近似的地方少划几份，不容易近似的地方多划几份。这就是所谓的“自适应”。

具体的话，就是设区间 [a,b] 的中点为 c，则当且仅当：

$\small |S(a,c)+S(c,b)-S(a,b)|<15Eps$

时(加==亦可)直接返回结果，否则递归调用，再次划分区间。递归调用时精度Eps也要相应地减小一半。 Ps：

$\small \int_a^bf(x)dx=\int_a^cf(x)dx+\int_c^bf(x)dx\ (a<c<b)$

这里的S(a,b) 就是 [a,b] 的三点辛普森公式值，返回的结果是S(c,b)+S(a,c)+Δs，Δs=[S(a,c)+S(c,b)−S(a,b)]/15。顺便提醒一句，如果直接返回 S(a,b) 的话，可能存在的误差超出可接受范围，就是比较可能会出错。还有这个 15 是怎么来的别问我。

三、总结

四、代码

double f(double x)
{
    return b * sqrt(1 - (x * x) / (a * a)); // 写要求辛普森积分的函数，如：椭圆公式 y 表达式
}

double simpson(double a, double b) // 三点辛普森积分法，要求f(x)是全局函数
{ 
    double c = a + (b - a) / 2;
    return (f(a) + 4 * f(c) + f(b)) * (b - a) / 6;
}

double integral(double L, double R, double Eps) // 自适应辛普森积分递归过程
{ 
    // 这里 mid 不能定义为全局变量，因为最后一条 return 有两个 mid 若是全局，第二个递归的 mid 会有更换
    double mid = L + (R - L) / 2;
    double ST = simpson(L, R), SL = simpson(L, mid), SR = simpson(mid, R);
    if(fabs(SL + SR - ST) <= 15 * Eps)  return SL + SR + (SL + SR - ST) / 15; // 直接返回结果
    // 若这里直接 return ST; 会 WA
    return integral(L, mid, Eps/2) + integral(mid, R, Eps/2); // 对半划分区间
}