3.【C++进阶】二叉搜索树

本博客梳理二叉搜索树基本概念及底层原理

一、二叉搜索树概念

1．根本法则：左<根<右

对这棵树而言，任意一个节点N，左子树的节点值小于N，右子树的节点值大于N

2．map/set系列容器的底层

map/set/multimap/multiset系列容器的底层就是二叉搜索树，map和set不支持插入相等值，multimap/multiset支持插入相等值

二、二叉搜索树性能

最差情况下，二叉搜索树变成单支树，则查找效率变成O(N)

三、二叉搜索树的底层原理

以下三个基本操作均有对应OJ题，点击即可跳转

1．二叉搜索树的查找

直接根据搜索树的性质查找即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        TreeNode* cur = root;
        while(cur)
        {
            if(val < cur->val)
                cur = cur->left;
            else if(val > cur->val)
                cur = cur->right;
            else
                return cur;
        }
        return nullptr;
    }
};

2．二叉搜索树的插入

（1）树为空，直接新增节点，赋值给root指针
（2）树不为空，按二叉搜索树性质寻找插入位置，找到空位置后插入新节点
（3）如果支持插入相等的值，则寻找插入位置时，需要统一向左or向右走，保持逻辑一致性

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution 
{
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) 
    {
        if(root == nullptr)
        {
            root = new TreeNode(val);
            return root;
        }

        TreeNode* cur = root;
        TreeNode* parent = nullptr;
        //寻找插入位置
        while(cur)
        {
            if(val < cur->val)
            {
                parent = cur;
                cur = cur->left;
            }
            else if(val > cur->val)
            {
                parent = cur;
                cur = cur->right;
            }
        }

        cur = new TreeNode(val);
        if(val < parent->val)
            parent->left = cur;
        else
            parent->right = cur;
        return root;
    }
};

3．二叉搜索树的删除

删除一个节点可能出现的四种情况：
（1）目标节点N左右孩子均为空
（2）目标节点N左为空，右不为空
（3）目标节点N右为空，左不为空
（4）目标节点N左右均不为空
对应解决方案
（1）情况1和情况2合并，把N的父亲指向N的右孩子，然后删除N

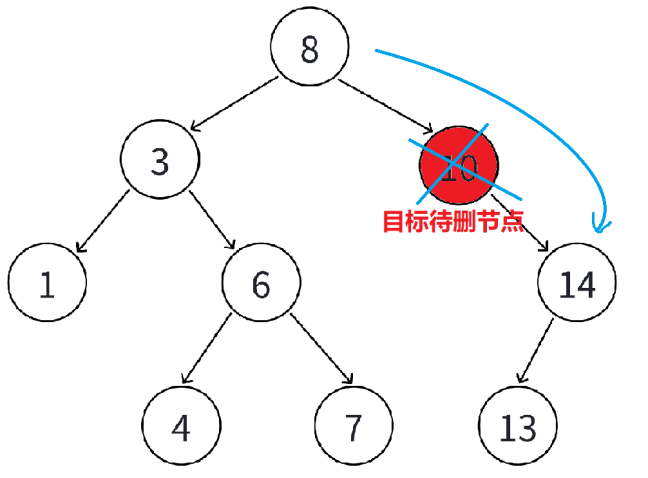
（2）情况3：把N的父亲指向N的左孩子，然后删除N

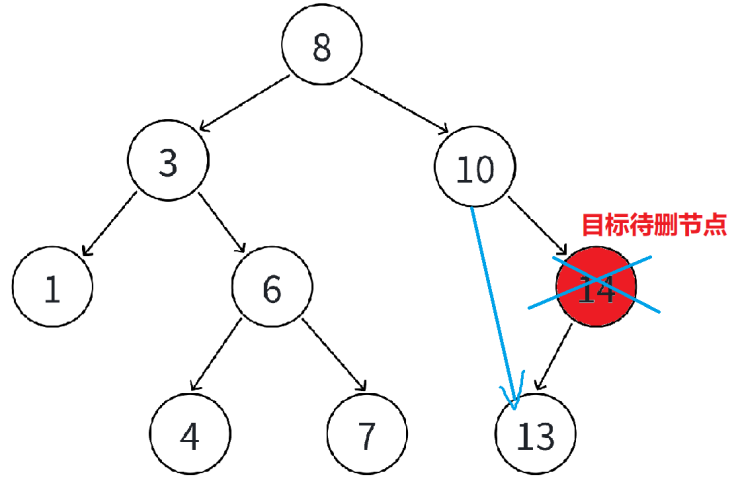
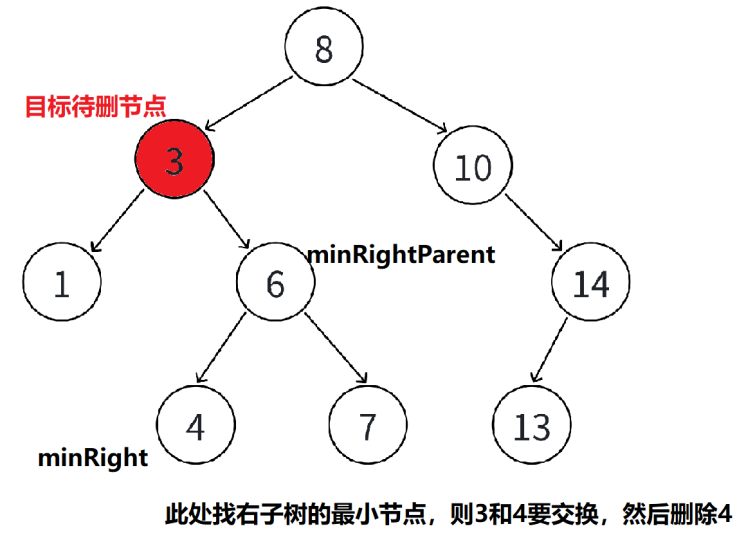
（3）情况4：采用替换法，找左子树的最大or右子树的最小来替换目标待删节点，然后目标待删节点会转换成上面的情况，再删除即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        //先查找key所在的位置
        TreeNode* parent = nullptr;
        TreeNode* cur = root;
        while(cur)
        {
            if(key < cur->val)
            {
                parent = cur;
                cur = cur->left;
            }
            else if(key > cur->val)
            {
                parent = cur;
                cur = cur->right;
            }
            else
            {
                //执行删除逻辑，然后跳出循环
                if(cur->left == nullptr)//左为空，右为空or不为空
                {
                    if(cur == root)//注意如果cur就是根，则没有parent，要特殊处理
                    {
                        root = cur->right;
                    }
                    else
                    {
                        if(cur == parent->left)
                            parent->left = cur->right;
                        else
                            parent->right = cur->right;
                    }
                    delete cur;
                }
                else if(cur->right == nullptr)//此时cur->left一定不为空
                {
                    if(cur == root)//注意如果cur就是根，则没有parent，要特殊处理
                    {
                        root = cur->left;
                    }
                    else
                    {
                        if(cur == parent->left)
                            parent->left = cur->left;
                        else
                            parent->right = cur->left;
                    }
                    delete cur;
                }
                else
                {
                    //找右的最小来替换当前cur
                    //转换成上面的情况
                    TreeNode* minRight = cur->right;
                    TreeNode* minRightParent = cur;

                    while(minRight->left)
                    {
                        minRightParent = minRight;
                        minRight = minRight->left;
                    }

                    swap(cur->val, minRight->val);

                    //注意minRight右可能不为空
                    if(minRight == minRightParent->left)
                        minRightParent->left = minRight->right;
                    else
                        minRightParent->right = minRight->right;
                    delete minRight;
                    
                }
                return root;
            }
        }
        return root;
    }
};