文章目录
Ch6. 数理统计
(一) 总体与样本
1.概念:
(1)总体
总体:研究对象的全体
个体:组成总体的每一个元素

(2)样本
简单随机样本,简称样本。样本与总体 独立同分布。(取自总体的样本,相互之间都独立,且与总体分布相同)

(3)样本的分布

2.性质:
设
X
1
,
X
2
,
X
3
,
.
.
.
,
X
n
(
n
>
1
)
X_1,X_2,X_3,...,X_n(n>1)
X1,X2,X3,...,Xn(n>1)为来自总体 N(μ,σ²) (σ>0)的简单随机样本(独立同分布),
X
‾
=
1
n
∑
i
=
1
n
X
i
\overline{X}=\dfrac{1}{n}\sum\limits_{i=1}^nX_i
X=n1i=1∑nXi,则有:
①
X
i
∼
N
(
μ
,
σ
2
)
X_i\sim N(μ,σ²)
Xi∼N(μ,σ2)
②
X
‾
∼
N
(
μ
,
σ
2
n
)
\overline{X} \sim N(μ,\dfrac{σ²}{n})
X∼N(μ,nσ2)
③
C
o
v
(
X
i
,
X
‾
)
=
σ
2
n
{\rm Cov}(X_i,\overline{X})=\dfrac{σ²}{n}
Cov(Xi,X)=nσ2
证明:
3.样本与总体 独立同分布,期望相同,方差也相同
①样本的期望与总体的期望相同:
E
(
X
i
)
=
E
(
X
)
E(X_i) = E(X)
E(Xi)=E(X),
∑
i
=
1
n
E
(
X
i
)
=
n
E
(
X
)
\sum\limits_{i=1}^nE(X_i) = nE(X)
i=1∑nE(Xi)=nE(X)
②样本的方差与总体的方差相同:
D
(
X
i
)
=
D
(
X
)
D(X_i) = D(X)
D(Xi)=D(X),
∑
i
=
1
n
D
(
X
i
)
=
n
D
(
X
)
\sum\limits_{i=1}^nD(X_i) = nD(X)
i=1∑nD(Xi)=nD(X)
(二) 统计量 (5个)
1.概念
(1)统计量的定义

(2)顺序统计量
| 顺序统计量 | 定义 | 分布函数 | 概率密度 |
|---|---|---|---|
| ①第n顺序统计量 X ( n ) X_{(n)} X(n) | max { X 1 , X 2 , . . . , X n } \max\{X_1,X_2,...,X_n\} max{X1,X2,...,Xn} | [ F ( x ) ] n [F(x)]^n [F(x)]n | n [ F ( x ) ] n − 1 f ( x ) n[F(x)]^{n-1}f(x) n[F(x)]n−1f(x) |
| ②第1顺序统计量 X ( 1 ) X_{(1)} X(1) | min { X 1 , X 2 , . . . , X n } \min\{X_1,X_2,...,X_n\} min{X1,X2,...,Xn} | 1 − [ 1 − F ( x ) ] n 1-[1-F(x)]^n 1−[1−F(x)]n | n [ 1 − F ( x ) ] n − 1 f ( x ) n[1-F(x)]^{n-1}f(x) n[1−F(x)]n−1f(x) |

2.常用统计量
①样本均值: X ˉ = 1 n ∑ i = 1 n X i \bar{X}=\dfrac{1}{n}\sum\limits_{i=1}^nX_i Xˉ=n1i=1∑nXi ∴ ∑ i = 1 n X i = n X ˉ \sum\limits_{i=1}^nX_i=n\bar{X} i=1∑nXi=nXˉ
②样本方差: S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S²=\dfrac{1}{n-1}\sum\limits_{i=1}^n(X_i-\bar{X})² S2=n−11i=1∑n(Xi−Xˉ)2 = 1 n − 1 ( ∑ i = 1 n X i 2 − n X ˉ 2 ) =\dfrac{1}{n-1}(\sum\limits_{i=1}^nX_i^2-n\bar{X}^2) =n−11(i=1∑nXi2−nXˉ2), E ( S 2 ) = σ 2 E(S^2)=σ² E(S2)=σ2
样本标准差: S = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S=\sqrt{\dfrac{1}{n-1}\sum\limits_{i=1}^n(X_i-\bar{X})²} S=n−11i=1∑n(Xi−Xˉ)2
③样本k阶(原点)矩: A k = 1 n ∑ i = 1 n X i k ( k = 1 , 2 , . . . ) A_k=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^k (k=1,2,...) Ak=n1i=1∑nXik(k=1,2,...)
④样本k阶中心矩: B k = 1 n ∑ i = 1 n ( X i − X ˉ ) k ( k = 2 , 3 , . . . ) B_k=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})^k(k=2,3,...) Bk=n1i=1∑n(Xi−Xˉ)k(k=2,3,...)
①k阶原点矩是 ( X i − 0 ) k (X_i-0)^k (Xi−0)k,k阶中心矩是 ( X i − X ˉ ) k (X_i-\bar{X})^k (Xi−Xˉ)k
②样本均值是一阶原点矩,二阶中心矩 B 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 = n − 1 n S 2 B_2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})²=\dfrac{n-1}{n}S^2 B2=n1i=1∑n(Xi−Xˉ)2=nn−1S2
(1)样本方差 S²
1.定义: S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ˉ ) 2 S^2=\dfrac{1}{n-1}\sum\limits_{i=1}^n(X_i-\bar{X})^2 S2=n−11i=1∑n(Xi−Xˉ)2
2.分布: n − 1 σ 2 S 2 ∼ χ 2 ( n − 1 ) \dfrac{n-1}{σ^2}S^2 \sim \chi^2(n-1) σ2n−1S2∼χ2(n−1)
3.数字特征: E ( S 2 ) = σ 2 , D ( S 2 ) = 2 σ 4 n − 1 E(S^2)=σ^2,D(S^2)=\dfrac{2σ^4}{n-1} E(S2)=σ2,D(S2)=n−12σ4

(2) X i − X ‾ X_i-\overline{X} Xi−X
1.结论:设
X
1
,
X
2
,
.
.
.
,
X
n
X_1,X_2,...,X_n
X1,X2,...,Xn为总体
X
∼
N
(
μ
,
σ
2
)
X\sim N(μ,σ²)
X∼N(μ,σ2)的简单随机样本,则:
①
C
o
v
(
X
i
,
X
‾
)
=
σ
2
n
{\rm Cov}(X_i,\overline{X})=\dfrac{σ²}{n}
Cov(Xi,X)=nσ2
② X i − X ‾ ∼ N ( 0 , n − 1 n σ 2 ) = N ( 0 , ( 1 − 1 n ) σ 2 ) X_i-\overline{X}\sim N(0,\dfrac{n-1}{n}σ²)=N(0,(1-\dfrac{1}{n})σ²) Xi−X∼N(0,nn−1σ2)=N(0,(1−n1)σ2)
③ S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 = n n − 1 ( X i − X ‾ ) 2 S^2=\dfrac{1}{n-1}\sum\limits_{i=1}^n(X_i-\overline{X})^2=\dfrac{n}{n-1}(X_i-\overline{X})^2 S2=n−11i=1∑n(Xi−X)2=n−1n(Xi−X)2
2.证明:
X
i
∼
N
(
μ
,
σ
2
)
,
X
‾
∼
N
(
μ
,
σ
2
n
)
X_i\sim N(μ,σ²),\overline{X}\sim N(μ,\dfrac{σ^2}{n})
Xi∼N(μ,σ2),X∼N(μ,nσ2)
由于
X
i
X_i
Xi与
X
‾
\overline{X}
X不独立,不满足独立可加性。
E
(
X
i
−
X
‾
)
=
E
(
X
i
)
−
E
(
X
‾
)
=
μ
−
μ
=
0
E(X_i-\overline{X})=E(X_i)-E(\overline{X})=μ-μ=0
E(Xi−X)=E(Xi)−E(X)=μ−μ=0
D
(
X
i
−
X
‾
)
=
D
(
X
i
)
+
D
(
X
‾
)
−
2
C
o
v
(
X
i
,
X
‾
)
=
σ
2
+
σ
2
n
−
2
×
σ
2
n
=
(
1
−
1
n
)
σ
2
=
n
−
1
n
σ
2
D(X_i-\overline{X})=D(X_i)+D(\overline{X})-2{\rm Cov}(X_i,\overline{X})=σ²+\dfrac{σ^2}{n}-2×\dfrac{σ²}{n}=(1-\dfrac{1}{n})σ²=\dfrac{n-1}{n}σ²
D(Xi−X)=D(Xi)+D(X)−2Cov(Xi,X)=σ2+nσ2−2×nσ2=(1−n1)σ2=nn−1σ2
∴
X
i
−
X
‾
∼
N
(
0
,
n
−
1
n
σ
2
)
X_i-\overline{X}\sim N(0,\dfrac{n-1}{n}σ^2)
Xi−X∼N(0,nn−1σ2)
例题1:24李林六(五)9.

分析:

答案:B
例题2:24李林四(一)10.

分析:

答案:B
3.矩的概念
①原点矩 A
| 样本k阶原点矩 A k A_k Ak | 总体k阶原点矩 |
|---|---|
|
A
1
=
1
n
∑
i
=
1
n
X
i
=
X
ˉ
A_1=\dfrac{1}{n}\sum\limits_{i=1}^nX_i=\bar{X}
A1=n1i=1∑nXi=Xˉ (样本一阶原点矩,即为均值) | E(X) |
| A 2 = 1 n ∑ i = 1 n X i 2 A_2=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^2 A2=n1i=1∑nXi2 | E(X²) |
| … | … |
| A k = 1 n ∑ i = 1 n X i k , k = 1 , 2 , . . . A_k=\dfrac{1}{n}\sum\limits_{i=1}^nX_i^k,k=1,2,... Ak=n1i=1∑nXik,k=1,2,... | E(Xk) |
②中心距 B
| 样本k阶中心矩 B k B_k Bk | 总体k阶中心矩 |
|---|---|
| B 1 = 1 n ∑ i = 1 n ( X i − X ˉ ) B_1=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X}) B1=n1i=1∑n(Xi−Xˉ) | E ( X − E X ) E(X-EX) E(X−EX) |
| B 2 = 1 n ∑ i = 1 n ( X i − X ˉ ) 2 = n − 1 n S 2 B_2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})²=\dfrac{n-1}{n}S^2 B2=n1i=1∑n(Xi−Xˉ)2=nn−1S2 | E [ ( X − E X ) 2 ] = D X E[(X-EX)²]=DX E[(X−EX)2]=DX |
| … | … |
| B k = 1 n ∑ i = 1 n ( X i − X ˉ ) k B_k=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})^k Bk=n1i=1∑n(Xi−Xˉ)k | E [ ( X − E X ) k ] E[(X-EX)^k] E[(X−EX)k] |
总体矩的矩估计量为样本矩:
①EX的矩估计量为
A
1
=
1
n
∑
i
=
1
n
X
i
=
X
ˉ
A_1=\dfrac{1}{n}\sum\limits_{i=1}^nX_i=\bar{X}
A1=n1i=1∑nXi=Xˉ
②DX的矩估计量为
B
2
=
1
n
∑
i
=
1
n
(
X
i
−
X
ˉ
)
2
=
n
−
1
n
S
2
B_2=\dfrac{1}{n}\sum\limits_{i=1}^n(X_i-\bar{X})²=\dfrac{n-1}{n}S^2
B2=n1i=1∑n(Xi−Xˉ)2=nn−1S2
(三) 抽样分布 (3个)
三大抽样分布,均与正态总体有关。总体与样本服从标准正态分布N(0,1)。
0.上α分位点
正态分布的上α分位点: Φ ( Z α 2 ) = 1 − α 2 Φ(Z_{\frac{α}{2}})=1-\dfrac{α}{2} Φ(Z2α)=1−2α


1.χ²分布
1.χ²分布的定义
若
X
1
∼
N
(
0
,
1
)
X_1\sim N(0,1)
X1∼N(0,1),则
X
1
2
∼
χ
2
(
1
)
X_1^2\sim χ^2(1)
X12∼χ2(1)
设X1,X2,…,Xn为正态总体N(0,1)的样本 (
X
i
X_i
Xi相互独立且同分布),则把统计量
χ
2
=
X
1
2
+
X
2
2
+
.
.
.
+
X
n
2
χ^2=X_1^2+X_2^2+...+X_n^2
χ2=X12+X22+...+Xn2
服从的分布称为 自由度为n的χ²分布,记作 χ²~χ²(n)
2.χ²分布的上α分位点
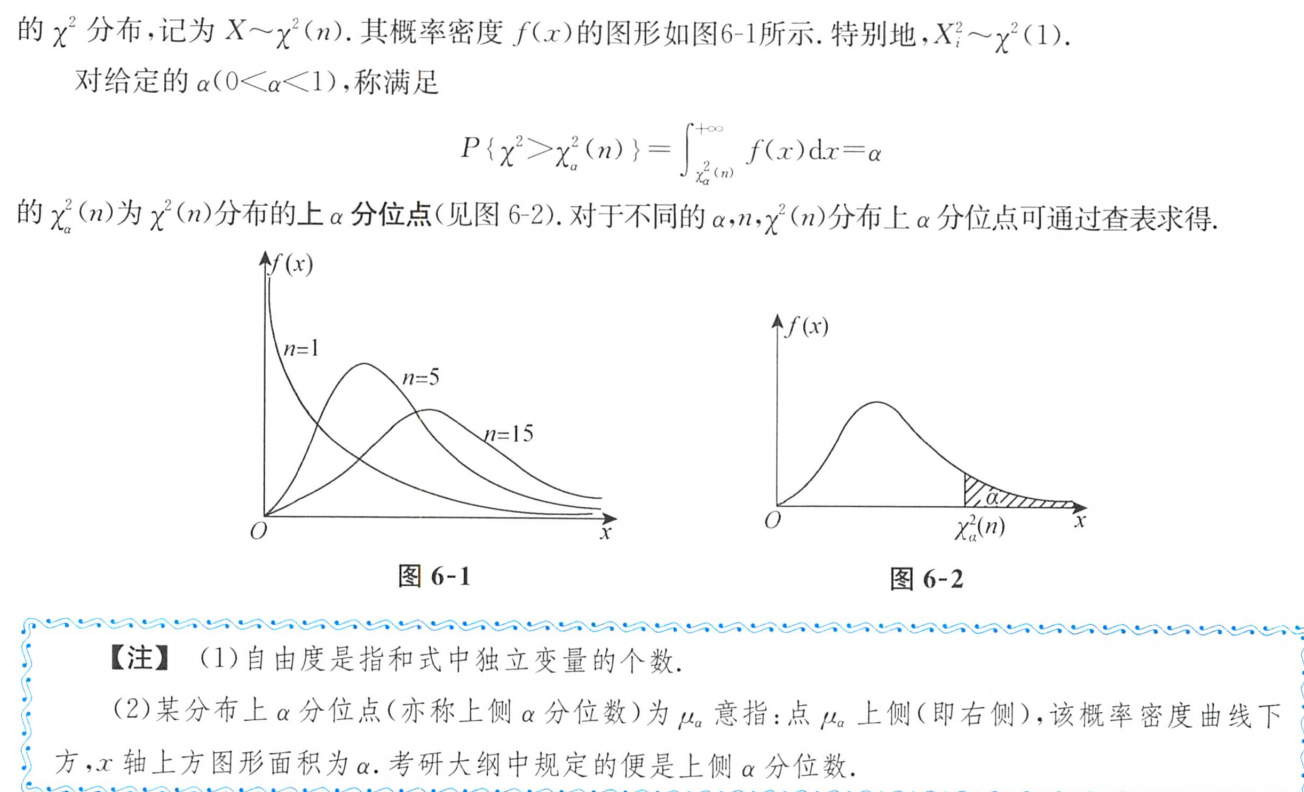
3.χ²分布的性质
- χ²分布的数字特征: E(χ²)=n,D(χ²)=2n
- χ²分布的独立可加性:设
χ
1
2
∼
χ
2
(
n
1
)
,
χ
2
2
∼
χ
2
(
n
2
)
χ²_1\sim χ²(n_1),χ²_2\sim χ²(n_2)
χ12∼χ2(n1),χ22∼χ2(n2),且
χ
1
2
χ²_1
χ12与
χ
2
2
χ²_2
χ22相互独立,则
χ
1
2
+
χ
2
2
∼
χ
2
(
n
1
+
n
2
)
χ²_1+χ²_2\simχ²(n_1+n_2)
χ12+χ22∼χ2(n1+n2)
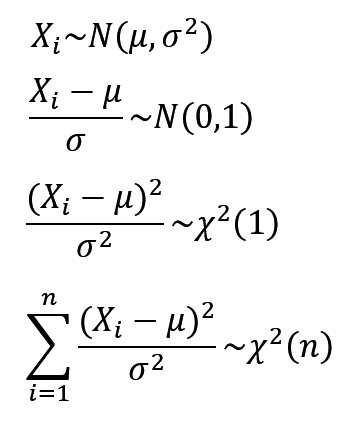
例题1:

分析:

答案: 1 20 \dfrac{1}{20} 201、 1 100 \dfrac{1}{100} 1001、2
2.t分布
1.t分布定义
设
X
∼
N
(
0
,
1
)
,
Y
∼
χ
2
(
n
)
X\sim N(0,1), Y\sim χ^2(n)
X∼N(0,1),Y∼χ2(n),且X,Y相互独立,则把统计量
t
=
X
Y
n
t=\dfrac{X}{\sqrt{\dfrac{Y}{n}}}
t=nYX
服从的分布称为自由度为n的t分布,记作
t
∼
t
(
n
)
t\sim t(n)
t∼t(n)
t(n)的概率密度h(t)关于t=0对称。当自由度n→∞时,t分布的极限就是标准正态分布,n≥30即可
2.t分布的上α分位点
x
=
t
α
(
n
)
x=t_α(n)
x=tα(n)右侧的面积(概率)为α,则称
t
α
(
n
)
t_α(n)
tα(n)为上α分位点
x = t 1 − α ( n ) x=t_{1-α}(n) x=t1−α(n)右侧的面积(概率)为1-α,则称 t 1 − α ( n ) t_{1-α}(n) t1−α(n)为上1-α分位点
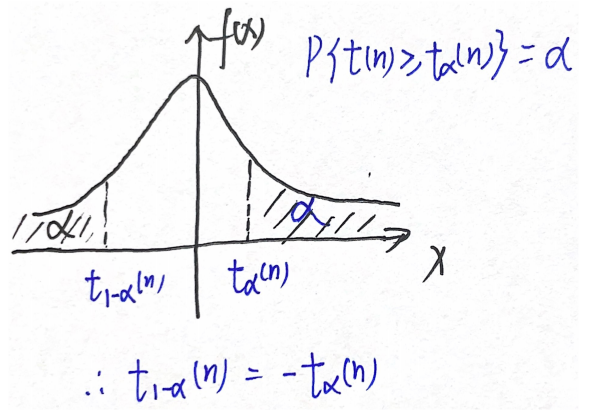
t分布的概率密度是偶函数
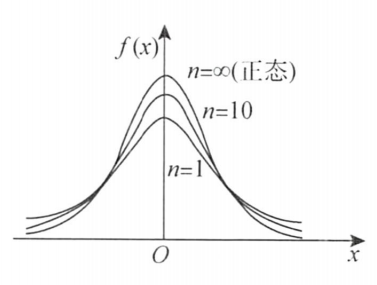
3.t分布性质
1.
E
(
t
)
=
0
E(t)=0
E(t)=0
2.上α分位点:
t
1
−
α
(
n
)
=
−
t
α
(
n
)
t_{1-α}(n)=-t_α(n)
t1−α(n)=−tα(n)
3.F分布
1.F分布定义
设
X
∼
χ
2
(
n
)
,
Y
∼
χ
2
(
m
)
X\sim χ^2(n),Y\sim χ^2(m)
X∼χ2(n),Y∼χ2(m),且X,Y相互独立,则把随机变量
F
=
X
n
Y
m
F=\dfrac{\dfrac{X}{n}}{\dfrac{Y}{m}}
F=mYnX
服从的分布称为自由度为(n,m)的F分布,其中n称为第一自由度,m称为第二自由度,记作 F ∼ F ( n , m ) F\sim F(n,m) F∼F(n,m)
2.F分布性质
1.若
F
∼
F
(
n
,
m
)
F\sim F(n,m)
F∼F(n,m),则
1
F
∼
F
(
m
,
n
)
\dfrac{1}{F}\sim F(m,n)
F1∼F(m,n)
2.上α分位点: 1 F α ( n , m ) = F 1 − α ( m , n ) \dfrac{1}{F_α(n,m)}=F_{1-α}(m,n) Fα(n,m)1=F1−α(m,n)
3.t分布与F分布的关系
若
t
∼
t
(
n
)
,则
t
2
∼
F
(
1
,
n
)
,
1
t
2
∼
F
(
n
,
1
)
若t\sim t(n),则t^2\sim F(1,n),\dfrac{1}{t^2}\sim F(n,1)
若t∼t(n),则t2∼F(1,n),t21∼F(n,1)
例题1:03年12. t分布与F分布的关系

分析:
X
∼
t
(
n
)
,
X
2
∼
F
(
1
,
n
)
,
1
X
2
∼
F
(
n
,
1
)
X\sim t(n),X²\sim F(1,n),\dfrac{1}{X²}\sim F(n,1)
X∼t(n),X2∼F(1,n),X21∼F(n,1)
答案:C
例题2:13年8.
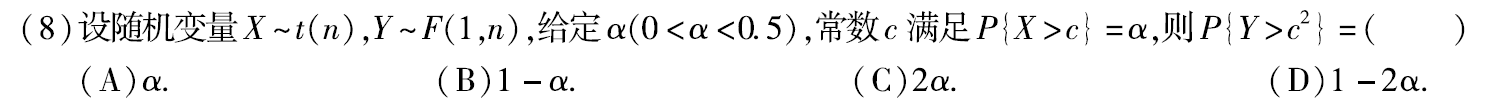
分析:X~t(n), 则 X²=Y~F(1,n)
∴P{Y>c²}=P{X²>c²}=P{X>c}+P{X<-c}=α+α=2α
答案:C
例题3:24李林六(四)8.

分析:

答案:C
(四) 抽样分布定理
设总体 X ∼ N ( μ , σ 2 ) X\sim N(μ,σ²) X∼N(μ,σ2),样本为 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn,独立同分布于总体
1.单个正态总体
1.样本均值:
X
ˉ
∼
N
(
μ
,
σ
2
n
)
\bar{X}\sim N(μ,\dfrac{σ²}{n})
Xˉ∼N(μ,nσ2),
X
ˉ
−
μ
σ
n
=
(
X
ˉ
−
μ
)
n
σ
∼
N
(
0
,
1
)
\dfrac{\bar{X}-μ}{\dfrac{σ}{\sqrt{n}}}=\dfrac{(\bar{X}-μ)\sqrt{n}}{σ}\sim N(0,1)
nσXˉ−μ=σ(Xˉ−μ)n∼N(0,1)
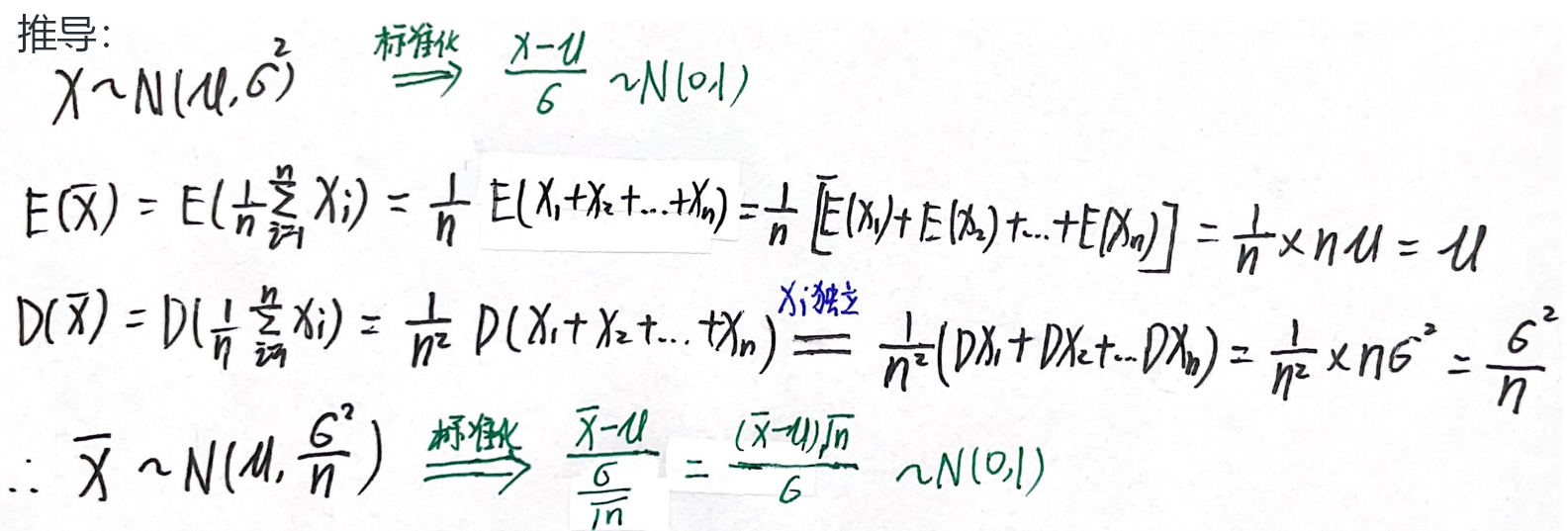
2. ∑ i = 1 n ( X i − μ σ ) 2 ∼ χ 2 ( n ) \sum\limits_{i=1}^n(\dfrac{X_i-μ}{σ})^2\sim \chi^2(n) i=1∑n(σXi−μ)2∼χ2(n)
3. ( n − 1 ) σ 2 S 2 \dfrac{(n-1)}{σ^2}S^2 σ2(n−1)S2 = 1 σ 2 ∑ i = 1 n ( X i − X ‾ ) 2 = ∑ i = 1 n ( X i − X ‾ σ ) 2 =\dfrac{1}{σ^2}\sum\limits_{i=1}^n(X_i-\overline{X})^2=\sum\limits_{i=1}^n(\dfrac{X_i-\overline{X}}{σ})^2 =σ21i=1∑n(Xi−X)2=i=1∑n(σXi−X)2 ∼ χ 2 ( n − 1 ) \sim \chi^2(n-1) ∼χ2(n−1)
∴ E ( S 2 ) = σ 2 , D ( S 2 ) = 2 σ 4 n − 1 E(S²)=σ²,D(S²)=\dfrac{2σ^4}{n-1} E(S2)=σ2,D(S2)=n−12σ4
S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 S^2=\dfrac{1}{n-1}\sum\limits_{i=1}^n(X_i-\overline{X})^2 S2=n−11i=1∑n(Xi−X)2
4.① n ( X ˉ − μ ) S ∼ t ( n − 1 ) \dfrac{\sqrt{n}(\bar{X}-μ)}{S}\sim t(n-1) Sn(Xˉ−μ)∼t(n−1)

5.样本均值 X ˉ \bar{X} Xˉ与样本方差 S 2 S^2 S2相互独立,即 E ( X ˉ S ) = E ( X ˉ ) E ( S ) E(\bar{X}S)=E(\bar{X})E(S) E(XˉS)=E(Xˉ)E(S)
例题1:17年8. 抽样分布定理

分析:

答案:B
例题2:05年14. 抽样分布定理、F分布

分析:
A.
n
X
‾
=
X
1
+
X
2
+
.
.
.
+
X
n
∼
N
(
0
,
n
)
n\overline{X}=X_1+X_2+...+X_n\sim N(0,n)
nX=X1+X2+...+Xn∼N(0,n)。A❌
B. n − 1 σ 2 S 2 = σ 2 = 1 ( n − 1 ) S 2 ∼ χ 2 ( n − 1 ) \dfrac{n-1}{σ^2}S^2\xlongequal{σ^2=1}(n-1)S^2\sim \chi^2(n-1) σ2n−1S2σ2=1(n−1)S2∼χ2(n−1),不是nS²。B❌
C. n ( X ‾ − μ ) s ∼ t ( n − 1 ) \dfrac{\sqrt{n}(\overline{X}-μ)}{s}\sim t(n-1) sn(X−μ)∼t(n−1)。应改为 n X ‾ S ∼ t ( n − 1 ) \dfrac{\sqrt{n}\overline{X}}{S}\sim t(n-1) SnX∼t(n−1)C❌
D:
X
i
∼
N
(
0
,
1
)
X_i\sim N(0,1)
Xi∼N(0,1),即
X
i
X_i
Xi服从标准正态分布
X
1
2
1
∑
i
=
2
n
X
i
2
n
−
1
∼
F
(
1
,
n
−
1
)
\dfrac{\frac{X_1^2}{1}}{\frac{\sum\limits_{i=2}^nX_i^2}{n-1}}\sim F(1,n-1)
n−1i=2∑nXi21X12∼F(1,n−1),D正确
答案:D
例题3:24李林四(三)9.

分析:
A.t(1)。分母是绝对值,一般都服从t(1)
B.
χ
2
(
1
)
\chi^2(1)
χ2(1)
D.F(1,3)

答案:C
例题4:24李林四(三)16、23李林四(四)16.
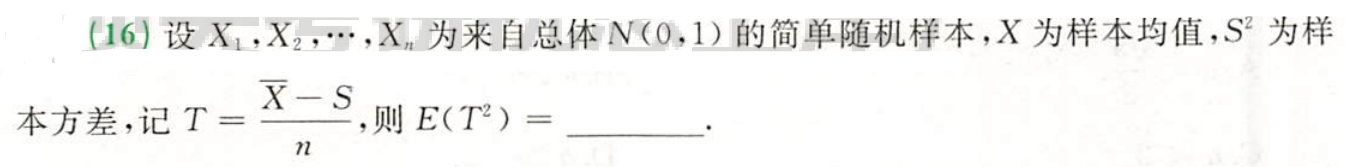
分析:样本均值 X ˉ \bar{X} Xˉ与样本方差 S 2 S^2 S2相互独立,即 E ( X ˉ S ) = E ( X ˉ ) E ( S ) E(\bar{X}S)=E(\bar{X})E(S) E(XˉS)=E(Xˉ)E(S)
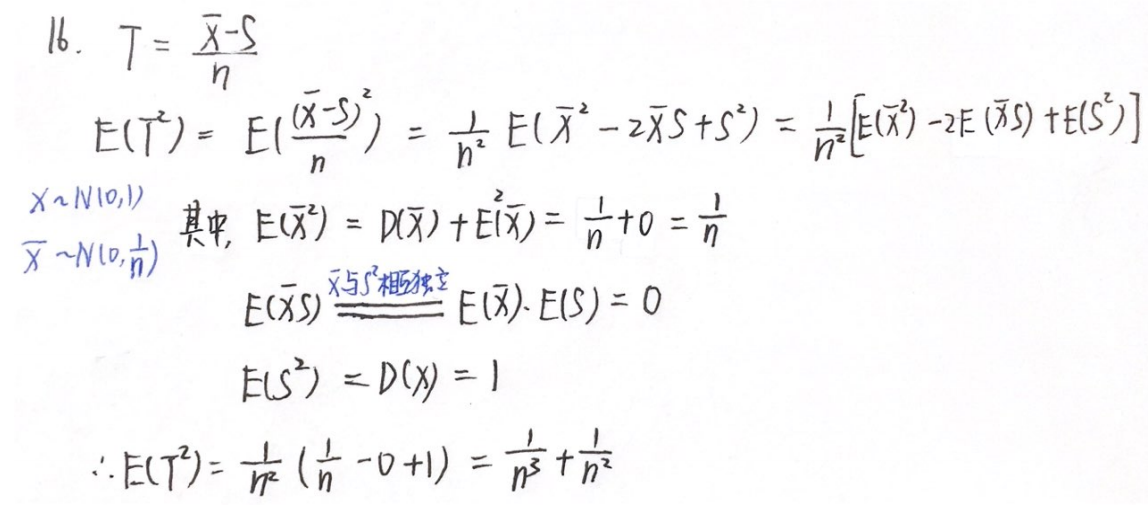
答案: 1 n 3 + 1 n 2 \dfrac{1}{n^3}+\dfrac{1}{n^2} n31+n21
2.两个正态总体
定理1:

定理2:

例题1:23李林六(六)10.

分析:
X与Y相互独立。则
X
‾
\overline{X}
X与
Y
‾
\overline{Y}
Y相互独立,则
X
‾
−
Y
‾
∼
N
(
0
,
2
σ
2
n
)
\overline{X}-\overline{Y}\sim N(0,\dfrac{2σ^2}{n})
X−Y∼N(0,n2σ2)。AB✔
C.
(
n
−
1
)
S
2
σ
2
=
∑
i
=
1
n
(
X
i
−
X
ˉ
σ
)
2
∼
χ
2
(
n
−
1
)
\dfrac{(n-1)S^2}{σ^2}=\sum\limits_{i=1}^n(\dfrac{X_i-\bar{X}}{σ})^2\simχ^2(n-1)
σ2(n−1)S2=i=1∑n(σXi−Xˉ)2∼χ2(n−1),且卡方分布具有独立可加性,∴C正确
D.应该改为2n-2
答案:D

























 396
396











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










