囫囵吞枣先学着,Simulink仿真慢慢啃 ⍢⃝
基本公式
对于电压方程:
可以理解为,线圈的电阻产生的压降+线圈感应出的各种电压。
感应电压又分为两部分,线圈磁链产生的部分以及由永磁体磁链产生的反电动势。参考PMSM的等效电路图:
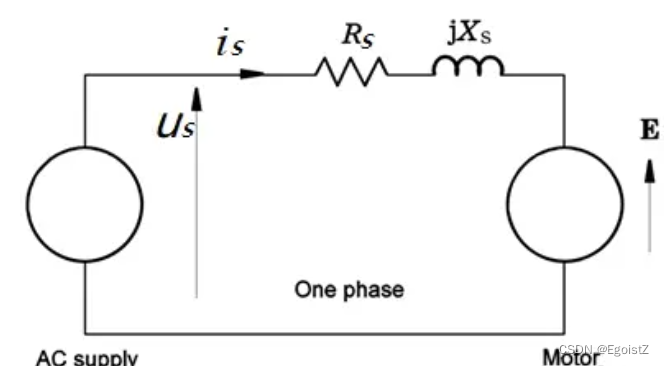
线圈电阻很好理解,关键是其中包含的磁链方程需要进一步推导和解释。对于磁链方程:
第一部分为线圈电流自感及线圈之间互感产生的磁链,因此
这个矩阵中会包含定子自感和互感的部分:


但实际上书上会将这部分表示为定子互感和定子漏感矩阵相加的的形式。这一部分有待考究,但总体来说结果都是一样的。我没有完全理解这一部分,因此按下不表。
磁链可以理解为单匝线圈的磁通量乘以匝数。单匝线圈磁通的来源为自身变化的电流。由法拉第电磁感应定律,磁通对时间的微分为电压,在这里,多个磁通合成的磁链对时间的微分也是电压,变成了的一部分。
第二部分为永磁体自带的磁链。这里表示为一个磁链系数矩阵,无单位,乘以为永磁体在每一相绕组中产生的磁链幅值。这个系数矩阵跟电机结构有关,主要是考虑到了电机各相之间的相位差,并且将永磁体以N极作参考轴的磁链投影到各自然轴上。对于结构相同的电机,这个系数矩阵都是恒定的。
双三相中的VSD数学建模
在电压和磁链方程中:
基于这个自然坐标系下的数学建模,下面开始进行VSD,即α-β,x-y,零序子空间三个子空间的解耦。电感这个矩阵没太搞明白,需要进一步理解。目前仅处于记结论状态。
采用VSD解耦控制,整体思路是,将六相abcxyz转化为α-β、x-y,零序子空间o1-o2,然后分别对每一相进行控制,其中,如果采用两个三相中性点隔离的双三相,则o1-o2为0,不需要控制,x-y对电机输出转矩和转速没有影响,只不过会导致输出电流波形产生变化。α-β则类似于三相电机的α-β静止两相坐标系。
书上这个矩阵是直接给的计算结果,也因此造成了不知道为什么谐波电流会对应到各个空间的疑惑。其实这个矩阵可以变成:
注意此处 k=1,3,5…,变换时要记得×三分之一,幅值不变。
其中推导省略,以上矩阵等效于所描述的坐标系经过推导,从自然坐标系变换到DQ等效于:
第一、二行即为dq坐标变换,与电角度有关。后两个子空间由于不参与能量变换,因此和电角度不挂钩。由这个公式去乘以自然坐标系下的电压矩阵,可以将6个自然相的电压解耦变成dq轴的恒定电压。基波和12k±1的谐波会落到这个子空间内。从后面加减的数值就可以看出,建立坐标系时就考虑了谐波的映射。
第三、四行为x-y子空间的坐标变换。x-y子空间为6k±1的谐波映射的空间。
第五、六行为零序子空间o1-o2。为6k±3谐波的映射。
基本上VSD建模的核心就是这个变换矩阵。从自然坐标系的六个耦合矢量解耦到三个子空间;其中子空间的建模依据是三相DQ坐标系的拓展,还是尝试将六相分解到只影响转矩的DQ轴上;其他的量被分到不同的子空间以代表不同的谐波,通过控制谐波空间以减少对电机控制的影响。
这个矩阵对后续四矢量SVPWM的调制至关重要。SVPWM的矢量合成就是通过这个矩阵来的。
四矢量SVPWM调制
双三相电机传统的双矢量SVPWM和三相电机的调制类似,仅为简单推广,仅考虑解耦到α-β子空间的部分,并利用这部分进行电压合成和跟踪。因此这里不细表,仅作四矢量调制的笔记。
电压矢量和开关状态可表示为如下。其中α代表30度的相角,其次数代表各相在自然坐标系中的位置。

根据六相电压源逆变器的结构,6个开关拥有2^6=64种开关状态。将6个开关状态以(000111)这样的二进制形式表示,并将其化为8进制数,表示某一个开关状态合成的矢量。注意这里的合成是分别指两个子空间内单独合成。四矢量的调制就是指后续将两个子空间同时考虑去合成参考电压矢量。
根据这俩公式,我们可以将自然坐标系内合成的矩阵根据对应空间的两行进行分解和绘图。得到α-β、x-y两个子空间内各开关状态对应的矢量图:


得到的是四种幅值的向量,且在α-β空间内最大的向量在x-y空间内最小。并且在α-β空间的Sector角度为30度,而在x-y空间为150度。这些都是根据这个公式计算出来的。用
这个矩阵进行计算也行,结果都是一样的。
四矢量SVPWM算法的核心思想是:由于六相PMSM 的机电能量转换只与α-β子空间上的电流矢量有关,在x-y子空间上的电流只产生谐波损耗,而传统的两矢量六相SVPWM 算法只考虑了对α-β子空间上的电压进行跟踪,没有考虑x-y子空间上的电压合成效果,这将会在x-y子空间上产生不必要的谐波损耗。换而言之,只要有电压矢量分到x-y子空间内,就会产生一定的谐波来影响电机控制。因此,四矢量SVPWM算法的电压矢量选取的标准为在一个开关周期内,在α-β子空间内合成的电压矢量最大,并且在x-y子空间内合成的电压矢量最小。四矢量SVPWM算法就是在两矢量六相SVPWM算法的基础上增加两个基本电压矢量,通过增加的电压矢量来抵消在x-y子空间上形成的电压作用效果。以下这个矩阵能很好的描述这个思想:
这里tk是作用在第k个电压矢量上的时间,k = 1,2,3,4;t0 为零矢量作用时间;右边的列向量代表参考电压在α轴和β轴上的投影。这里的次数代表着第几个矢量;下标代表着矢量在哪个轴的投影;和
表示参考电压矢量在α-β轴上的投影;0表示0矢量以及在x-y子空间上合成的电压矢量应该为0以保证谐波损耗最小。
四个矢量的选取准则是:单个扇区内,选取α-β子空间内幅值最大的个电矢量,以及这电压矢量在x-y子空间对应为幅值最小的矢量。各矢量作用时间可推导为:
遵照电压源逆变器开关次数最少原则添加零矢量并调整作用时间。这部分书上没有给推导,我自己也没有研究明白,因此先记结论:
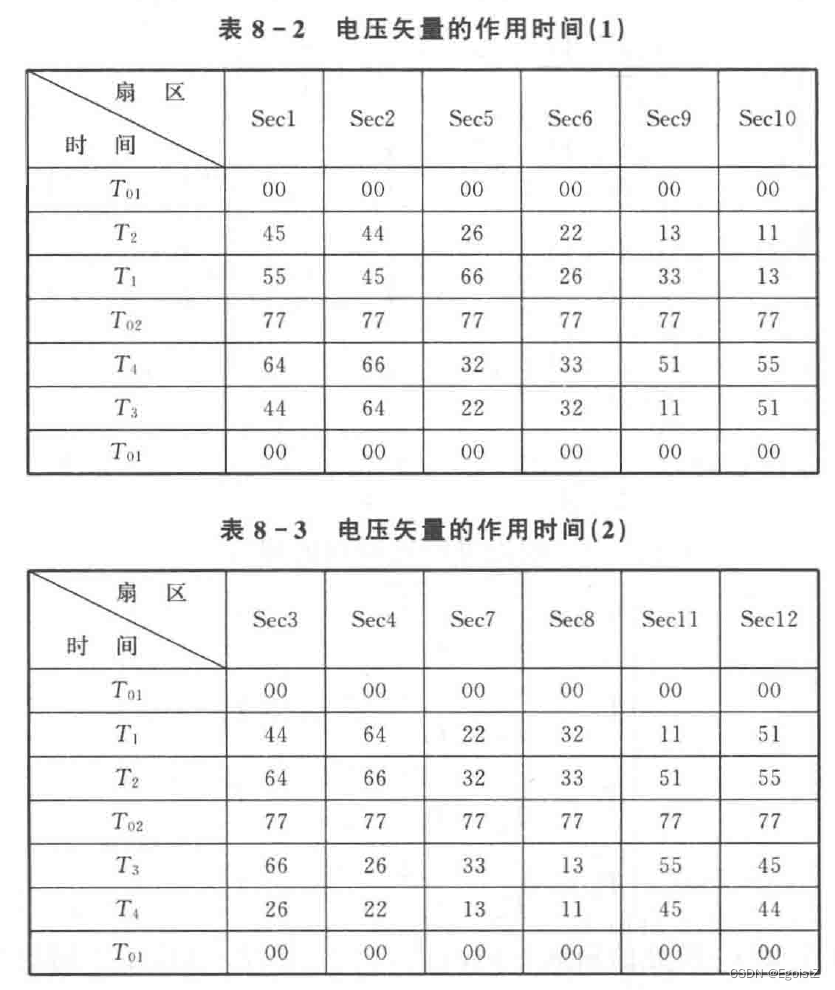







 本文详细探讨了PMSM电机的电压和磁链方程,特别是VSD建模中的磁链矩阵,以及四矢量SVPWM算法如何通过解耦和选择合适的电压矢量来减少谐波损耗。作者解释了α-β、x-y子空间的原理,并给出了电压矢量选择和零矢量处理的原则。
本文详细探讨了PMSM电机的电压和磁链方程,特别是VSD建模中的磁链矩阵,以及四矢量SVPWM算法如何通过解耦和选择合适的电压矢量来减少谐波损耗。作者解释了α-β、x-y子空间的原理,并给出了电压矢量选择和零矢量处理的原则。
















 7756
7756

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








