【无码专区8】三角形二维数点——计数有多少个给定点落在三角形区域内

本文链接：https://blog.csdn.net/Emm_Titan/article/details/121222501

因为只有std，没有自我实现，所以是无码专区

主要是为了训练思维能力

solution才是dls正解，但是因为只有潦草几句，所以大部分会有我自己基于正解上面的算法实现过程，可能选择的算法跟std中dls的实现不太一样。

std可能也会带有博主自己的注释。

problem

平面上有 $n$ 个点， $x_i,y_i)$ 。

$q$ 次询问，每次给定三个点 $A (x + d, y), B (x, y), C (x, y + d)$ 。

求有多少个点 $x_i,y_i)$ 在这个三角形内部或边界上。

$10s,128MB,all\le 1e6$ 。

my idea

给定的三角新很有特点：是等腰直角三角形且直角边分别与一条坐标轴平行。

并不是任意的一个三角形。那么这个三角形最难处理的自然就是斜边部分，因为不与坐标轴平行。

如果这是个正方形，就是个很简单的二维差分数点问题。

我曾试图用所有的点减去没有落在指定区域的点，但是发现外围图形仍然会被切割成若干个矩形和一个三角形，还是不会计算三角形。❌

我曾试图计算一个点的位置会被多少个三角形覆盖，对这些三角形贡献 $1$ 。但是查询的三角形压根不能找到一种范围限制能够说明：横纵坐标简单的加减为某个范围时属于这个三角形。❌

这两种思路都卡在了三角形重叠部分，更具体而言是没有找到要贡献的点坐标的特征性，显然这应该是正解的思路，这导致我们只能尝试不是正解的想法看能否优化跑过。

既然题目给的是平行坐标轴的直角三角形，那么这个直角边一定是切入点。

三角形不好做，但是四边形好做。

将三角形划分成一个四边形，和两个三角形。

如图：一个三角形存在很多种切割方式。

在这里插入图片描述

四边形是很容易计算的，三角形就递归地切割。所以时间复杂度是跟这个三角形切割挂钩的。

出于平衡左右时间的思想，我们肯定会选取“正半分”，使得两个三角形“完全一样”。

【但是如果只计算整点，“正半分”可能是分数，所以是尽可能地“正半分”，让两边地效率尽可能平衡。】

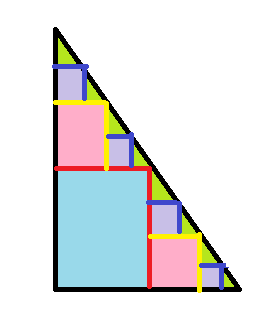
在这里插入图片描述

这种递归思想就是——分治。

没错，我们可以采取分而治之的做法，递归求解计算。

最底层的出口就是直角边某一条长度为 $1$ 的三角形，统计另一条边的贡献即可。

这样，划分最多 $l o g$ 层。

四边形的计算由于 $N\times M$ 根本开不下，无法预处理然后 $O (1)$ 差分求解。

只能采取数据结构计算。

具体而言：

将 $n$ 个点按 $x$ 第一关键字， $y$ 第二关键字排序。

需要在划分的一个区间内查询一个区间的问题。又是它！——主席树。

以 $y$ 建立线段树，第 $i$ 个版本维护的是前 $i$ 个点的主席数信息，权值线段树。

线段树上节点维护 $y\in[l,r]$ 的点有多少个。

$i\rightarrow i+1$ ，单点更新 $y_i$ 。

查询 $(x 1, y 1, x 2, y 2)$ 。找到 $x1<x_l$ 的最小 $l$ ，以及 $x r < x 2$ 的最大 $r$ 。二分查找。

然后就询问 $l\sim r$ 版本中 $[y 1, y 2]$ 内点的个数。

这样来看数据结构自带两个 $l o g$ ，外层还有一个。时间复杂度是 $O(nlog^3n)$ 的。

只能堪堪通过 $70\%$ 的数据点 $2\times 10^5$ 。

【计算出来大概是 $8 e 8$ 的， $10 s$ 跑 $1 e 9$ ，常数小写得好看应该是能跑过的。】

考虑优化，优化掉二分查找的 $l o g$ 。

最开始排序的 $l o g$ 省不了。

对于 $i$ ，直接二分找 $l, r$ 记录下来 $L_i,R_i$ 。

这样是将里面嵌套的 $l o g$ 放在了外面。

$O(n\log^3n)\rightarrow O(n\log^2n+n\log n)$ 。

就是两个 $l o g$ 的了。

算出来 $4 e 8$ ，相对与 $1 e 9$ 而言应该是绰绰有余的，常数大点应该没关系。

trick：图上一条线段分裂，但实际上计算的时候并不重叠。

中间界可以划给三角形部分，也可以是矩形部分。

但具体实现会发现，将中间界划分给三角形会比较好算，因为是封闭的。

不好说明，给图直观感受。

但是也不是说不能写，应该也是能实现的。

solution

直接查询，就是三维数点问题。 $C D Q$ 分治做 $O(n\log^2n)$ 。

~~又来了，一句话一页阐释。~~

为什么是三维数点？？怎么数？？

扩展：如何用三角形的三个坐标表示三角形中任意一点的坐标。

假设三角形三点分别为 $A (x 1, y 1), B (x 2, y 2), C (x 3, y 3)$ ，现要表示内部点 $O (x, y)$ 。

设射线 $A O$ 交 $B C$ 与点 $D$ ， $\vec{AO}=m\vec{AD},\vec{BD}=n\vec{BC}$ 。

则 $\vec{AO}=m\vec{AD}=m(\vec{AB}+\vec{BD})=m\vec{AB}+mn\vec{BC}$ 。

即：
$(x - x 1, y - y 1) = m (x 2 - x 1, y 2 - y 1) + m n (x 3 - x 2, y 3 - y 2)$

$= (m (x 2 - x 1) + m n (x 3 - x 2), m (y 2 - y 1) + m n (y 3 - y 2))$

$\Rightarrow\begin{cases}x-x1=m(x2-x1)+mn(x3-x2)\Rightarrow x=x1(1-m)+x2(m-mn)+x3mn\\y-y1=m(y2-y1)+mn(y3-y2)\Rightarrow y=y1(1-m)+y2(m-mn)+y3mn\\\end{cases}$

换元表示 $a = 1 - m, b = m - m n$ ，则
$\begin{cases}x=a·x1+b·x2+(1-a-b)x3\\y=a·y1+b·y2+(1-a-b)y3\\\end{cases}$

dbq，我确实没看懂这个三维数点怎么做。

观察性质，三角形区域 $(x^{'}, y^{'}) - (x^{'} + d, y^{'}) - (x^{'}, y^{'} + d)$ 。
相当于总区域减去 $x < x^{'}, y < y^{'}, x + y > x^{'} + y^{'} + d$ 三个半平面。
然后补上三个被减了两次的区域。
即 $x<x'\wedge y<y',x<x'\wedge x+y>x'+y'+d',y<y'\wedge x+y>x'+y'+d$ 。

这三个部分都是二维数点，直接做，时间复杂度 $O(n\log n)$ 。

其实看题解的时候我并不懂，但是一看代码就懂了！！

原来是我不会等腰直角三角形的二维数点！！其实很简单。

code

在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;
#define FOR(a,b,c) for (int a=b,_c=c;a<=_c;a++)
#define FORD(a,b,c) for (int a=b;a>=c;a--)
#define REP(i,a) for(int i=0,_a=(a); i<_a; ++i)
#define REPD(i,a) for(int i=(a)-1; i>=0; --i)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define sz(a) int(a.size())
#define reset(a,b) memset(a,b,sizeof(a))
#define oo 1000000007

using namespace std;

typedef long long ll;
typedef pair<int, int> pii;

const int maxn = 1000007;
const int maxv = 1000007;

int n, q, BIT[maxn], ans[maxn];
struct node {
	int x, y, d, id;
} a[maxn * 2];

bool cmp1(const node &a, const node &b) {
	return a.y < b.y || (a.y == b.y && a.id > b.id);
}

bool cmp2(const node &a, const node &b) {
	int v1 = a.x + a.y + a.d;
	int v2 = b.x + b.y + b.d;
	return v1 < v2 || (v1 == v2 && a.id < b.id);
}

void update(int p) {
	for (int i = p; i <= maxv; i += i & (-i))
		BIT[i]++;
}

int get(int p) {
	int ans = 0;
	p = min(p, maxv);
	for (int i = p; i; i -= i & (-i))
		ans += BIT[i];
	return ans;
}

int main() {
	freopen("triangular.in", "r", stdin);
	freopen("triangular.out", "w", stdout);
	scanf("%d%d", &n, &q);
	FOR(i, 1, n) {
		scanf("%d%d", &a[i].x, &a[i].y);
		a[i].id = 0;
	}
	FOR(i, 1, q) {
		scanf("%d%d%d", &a[i + n].x, &a[i + n].y, &a[i + n].d);
		a[i + n].id = i;
	}
	sort(a + 1, a + n + q + 1, cmp1);
	FOR(i, 1, n + q)
	if (a[i].id)
		ans[a[i].id] -= get(a[i].x + a[i].d) - get(a[i].x - 1);
	else
		update(a[i].x);
	sort(a + 1, a + n + q + 1, cmp2);
	reset(BIT, 0);
	FOR(i, 1, n + q)
	if (a[i].id)
		ans[a[i].id] += get(a[i].x + a[i].d) - get(a[i].x - 1);
	else
		update(a[i].x);
	FOR(i, 1, q) printf("%d\n", ans[i]);
	return 0;
}