BZOJ2208: [Jsoi2010]连通数

题目链接

【分析】

刚开始看到这道题感觉挺蠢得。。缩点DAG就好了嘛。很迅速的打完后发现WA掉了。原因很简单，因为直接拓扑排序中dp更新答案会导致重复计算。
然后想办法改进。直接更新答案会重复计算，那如果记录下有那些点已经更新了当前点就可以了。首先想到的就是直接用数组标记。。（那和暴力有什么区别！！？）。虽然暴力好像能过。。但是这显然不是我们想要的解法。
然后发现bitset好像可以完美解决。。但是刚打完发现我又错了。。
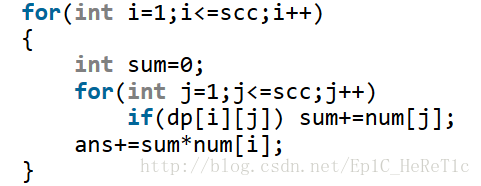
一开始统计答案的时候我用的是ans+=num[i]*dp[i].count();（num[i]是第i个强连通分量中节点的个数）。改正后正确的写法应该是：

之前那个错在哪里呢？也很简单。因为dp[i][j]=1表示i可以由j到达。是j对答案的贡献，而一开始的做法是把它当成了i对答案的贡献，显然错误。（蠢啊QnQ）

【代码】

1. 以前打的暴力

#include <iostream>
#include <algorithm>
#include <queue>
#include <cstring>
#include <cstdio>
#include <stack>
#include <cmath>
#include <vector>
#define N 300005
#define M 100005
#define INF 1<<30
#define T 100001
using namespace std;

inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

int n,ans;
char s[2010];
int flag[2010],cnt[2010];
int e[2010][2010];

void dfs(int x)
{
    flag[x]=1;
    ans++;
    for(int i=cnt[x];i;i--)
    {
        int v=e[x][i];
        if(!flag[v])
            dfs(v);
    }
}

int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        scanf("%s",s+1);
        for(int j=1;j<=n;j++)
            if(s[j]=='1')
                e[i][++cnt[i]]=j;
    }
    for(int i=1;i<=n;i++)
    {
        memset(flag,0,sizeof(flag));
        dfs(i);
    }
    printf("%d",ans);
    return 0;
}

1. bitset解法

#include <cstdio>
#include <iostream>
#include <queue>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <stack>
#include <bitset>
#define N 2005
#define M 4000005
#define INF 1000000000
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pa;

int read()
{
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

int n,ind,scc,cnt,ans,lim;
int low[N],dfn[N],Belong[N],in[N],num[N];
int b[M],p[N],nextedge[M];
bool Instack[N];
stack<int>st;
vector<int>g[N];
bitset<N>dp[N];

void Add(int x,int y)
{
    cnt++;
    b[cnt]=y;
    nextedge[cnt]=p[x];
    p[x]=cnt;
}

void Input_Init()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        char ch[2010];
        scanf("%s",ch+1);
        for(int j=1;j<=n;j++)
            if(ch[j]=='1') Add(i,j);
    }
}

void Tarjan(int x)
{
    dfn[x]=low[x]=++ind;
    st.push(x);Instack[x]=1;
    for(int i=p[x];i;i=nextedge[i])
    {
        int v=b[i];
        if(!dfn[v])
        {
            Tarjan(v);
            low[x]=min(low[x],low[v]);
        }
        else if(Instack[v]) low[x]=min(low[x],dfn[v]);
    }
    if(dfn[x]==low[x])
    {
        scc++;
        int now=-1;
        while(now!=x)
        {
            now=st.top();st.pop();
            Belong[now]=scc;
            Instack[now]=0;
            num[scc]++;
        }
    }
}

void Build_Graph()
{
    for(int i=1;i<=n;i++)
    for(int j=p[i];j;j=nextedge[j])
        if(Belong[i]!=Belong[b[j]]) g[Belong[i]].push_back(Belong[b[j]]),in[Belong[b[j]]]++;
}

void Solve()
{
    queue<int>q;
    for(int i=1;i<=scc;i++) 
    {
        if(!in[i]) q.push(i);
        dp[i][i]=1;
    }
    while(!q.empty())
    {
        int k=q.front();q.pop();
        for(int i=0;i<g[k].size();i++)
        {
            int v=g[k][i];
            dp[v]|=dp[k];
            in[v]--;if(!in[v]) q.push(v);
        }
    }
    for(int i=1;i<=scc;i++)
    {
        int sum=0;
        for(int j=1;j<=scc;j++)
            if(dp[i][j]) sum+=num[j];
        ans+=sum*num[i];
    }
    printf("%d\n",ans);
}

int main()
{
    Input_Init(); 
    for(int i=1;i<=n;i++) if(!dfn[i]) Tarjan(i);
    Build_Graph();
    Solve();
    return 0;
}