E. Cyclic Components
You are given an undirected graph consisting of n vertices and m edges. Your task is to find the number of connected components which are cycles.
Here are some definitions of graph theory.
An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex a is connected with a vertex b, a vertex b is also connected with a vertex a). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.
Two vertices uand v belong to the same connected component if and only if there is at least one path along edges connecting u and v.
A connected component is a cycle if and only if its vertices can be reordered in such a way that:
- the first vertex is connected with the second vertex by an edge,
- the second vertex is connected with the third vertex by an edge,
- ...
- the last vertex is connected with the first vertex by an edge,
- all the described edges of a cycle are distinct.
A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.
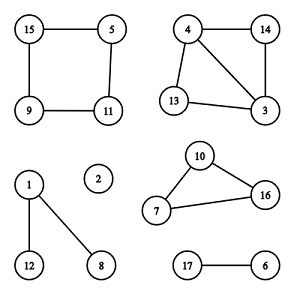
There are 6connected components, 2 of them are cycles: [7,10,16] and [5,11,9,15]
.
Input
The first line contains two integer numbers n and m (1≤n≤2⋅105, 0≤m≤2⋅105) — number of vertices and edges.The following m lines contains edges: edge i is given as a pair of vertices vi, ui (1≤vi,ui≤n, ui≠vi). There is no multiple edges in the given graph, i.e. for each pair (vi,ui) there no other pairs (vi,ui) and (ui,vi) in the list of edges.
Output
Print one integer — the number of connected components which are also cycles.
Examples
Input
5 4
1 2
3 4
5 4
3 5
Output
1
Input
17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6
Output
2
Note
In the first example only component [3,4,5]is also a cycle.
The illustration above corresponds to the second example.
题目大意:给出一个无向图(可能是几个连通的部分),找出是环的连通部分(注意:只是一个环,n 个点 n 条边那种,不能有多余的部分)。
无向图DFS时只有树边和返祖边,每次有返祖边时则证明出现了一个环,保证每个连通部分只有一个环且该连通部分每个点的度数为偶数即可。
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn = 2 * 1e5 + 5;
vector<int> G[maxn];
bool vis[maxn];
int dfs[maxn];
int dfs_time = 0;
int ans;
bool check;
void DFS(int x,int fa)
{
dfs[x] = ++dfs_time;
int len = G[x].size();
if(len & 1) check = false;
for(int i = 0;i < len; ++i)
{
int u = G[x][i];
if(!vis[u])
{
vis[u] = true;
DFS(u,x);
}
else if(vis[u] && u != fa && dfs[x] > dfs[u]) ++ans;
}
}
int main()
{
int n,m;
int result = 0;
scanf("%d %d",&n,&m);
int x,y;
for(int i = 0;i < m; ++i)
{
scanf("%d %d",&x,&y);
G[x].push_back(y);
G[y].push_back(x);
}
for(int i = 1;i <= n; ++i)
{
if(!vis[i])
{
ans = 0;
check = true;
vis[i] = true;
DFS(i,0);
if(ans == 1 && check) ++result;
}
}
printf("%d\n",result);
return 0;
}<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn = 2 * 1e5 + 5;
vector<int> G[maxn];
bool vis[maxn];
int dfs[maxn];
int dfs_time = 0;
int ans;
bool check;
void DFS(int x,int fa)
{
dfs[x] = ++dfs_time;
int len = G[x].size();
if(len & 1) check = false;
for(int i = 0;i < len; ++i)
{
int u = G[x][i];
if(!vis[u])
{
vis[u] = true;
DFS(u,x);
}
else if(vis[u] && u != fa && dfs[x] > dfs[u]) ++ans;
}
}
int main()
{
int n,m;
int result = 0;
scanf("%d %d",&n,&m);
int x,y;
for(int i = 0;i < m; ++i)
{
scanf("%d %d",&x,&y);
G[x].push_back(y);
G[y].push_back(x);
}
for(int i = 1;i <= n; ++i)
{
if(!vis[i])
{
ans = 0;
check = true;
vis[i] = true;
DFS(i,0);
if(ans == 1 && check) ++result;
}
}
printf("%d\n",result);
return 0;
}








 本文介绍了一种算法,用于确定给定无向图中哪些连通部分形成环状结构。通过深度优先搜索(DFS)检查每个连通部分是否仅包含一个环且所有顶点度数均为偶数。
本文介绍了一种算法,用于确定给定无向图中哪些连通部分形成环状结构。通过深度优先搜索(DFS)检查每个连通部分是否仅包含一个环且所有顶点度数均为偶数。
















 648
648

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








