八种常用排序算法总结

最新推荐文章于 2022-05-03 16:00:55 发布

Euadvancer

最新推荐文章于 2022-05-03 16:00:55 发布

阅读量519

点赞数 1

分类专栏：算法文章标签：排序算法 python

本文链接：https://blog.csdn.net/Euadvancer/article/details/55522083

版权

算法专栏收录该内容

0 篇文章 0 订阅

订阅专栏

总结
交换排序
- 一冒泡排序
- 二快速排序
选择排序
- 一直接选择排序
- 二堆排序
插入排序
归并排序
计数排序
基数排序

总结

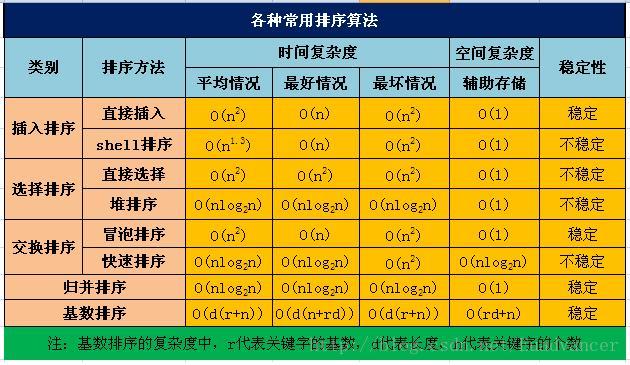
summary

稳定排序：冒泡排序，插入排序，归并排序，计数排序，基数排序
不稳定排序：选择排序，快速排序，堆排序

效率上，基于比较的方法中快速排序是最快的方法，平均时间复杂度为O(nlogn)，而不基于比较的基数排序的时间复杂度是O(n)，虽然它看起来更快，实际上快速排序可以适应更多随机化数据，且占的内存低于基数排序，所以快速排序更流行。

交换排序

一. 冒泡排序

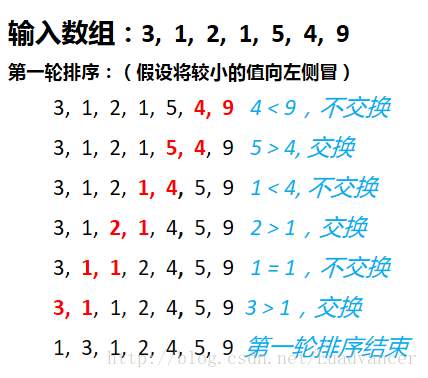
主要思路：它对相邻的两个数进行比较，如果发现它们的大小与排序要求相反时，就将它们互换，达到将较小（大）的数冒出来的效果
特点：稳定排序（从例子可以看出，在排序的过程中不会改变两个重复数字的顺序），不占用额外的内存

代码：

def BubbleSort(alist):
    for i in range(len(alist)):
        for j in range(len(alist) - 1, i, -1):
            if alist[j] < alist[j - 1]:
                alist[j], alist[j - 1] = alist[j - 1], alist[j]
    return alist

二. 快速排序

主要思路：
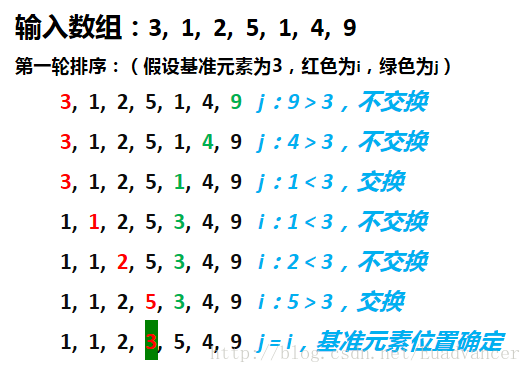
1. 首先选择一个基准元素（一般选择第一个或最后一个元素）
2. 找到基准位置在其排好序后的正确位置
3. 以基准元素的正确位置为分割线将原数组分为两部分，然后以相同方法进行排序直到所有元素排序完成
那么根据上述思路，快速排序的主体代码如下：
```
def QuickSort(alist):
    if len(alist) <= 1: return alist  # 如果没有元素或只有一个元素，直接返回
    privot = getPartition(alist)  # 得到基准元素索引
    left = QuickSort(alist[:privot])  # 根据基准元素索引划分，其左边的元素继续寻找基准元素
    right = QuickSort(alist[privot + 1:])  # 根据基准元素索引划分，其右边的元素继续寻找基准元素
```
现在问题就是如何得到基准元素的正确位置，也就是如何实现getPartition函数。思路如下：以两个索引i，j分别从数组的两边向中间搜索，即i = 0, j = len(input_array) - 1，i索引的目的是寻找大于基准元素的元素，j的目的是寻找小于基准元素的元素，每当i或j找到自己的目标则交换i，j的位置直到i == j
特点：不稳定排序（从上面的例子就能看到，在找到基准元素位置的过程中，后面一个1最终在前一个1的前面），不需要额外的内存（不考虑递归的栈内存）

代码：

def QuickSort(alist):
    """
    分为3步：
        1. 找到当前基准元素的索引
        2. 计算基准元素左侧元素的索引
        3. 计算基准元素右侧元素的索引
    :param alist: 
    :return:
    """
    if len(alist) <= 1: return alist  # 如果没有元素或只有一个元素，直接返回
    privot = getPartition(alist)  # 得到基准元素索引
    left = QuickSort(alist[:privot])  # 根据基准元素索引划分，其左边的元素继续寻找基准元素
    right = QuickSort(alist[privot + 1:])  # 根据基准元素索引划分，其右边的元素继续寻找基准元素
    return left + [alist[privot]] + right  # 返回排序后的结果


def getPartition(alist):
    """
    得到基准元素索引
    :param alist:
    :return:
    """
    privotKey = alist[0]  # 以第一个元素作为基准点
    i = 0  # 寻找小于基准点的元素
    j = len(alist) - 1  # 寻找大于基准点的元素
    while(i < j):
        while(alist[j] >= privotKey  and i < j): j -= 1  # j从右向左走，直到它小于基准点
        alist[i], alist[j] = alist[j], alist[i]  # 交换i, j元素
        while(alist[i] <= privotKey  and i < j): i += 1  # i从左向右走，直到它大于基准点
        alist[i], alist[j] = alist[j], alist[i]  # 交换i, j元素
    return i

选择排序

一. 直接选择排序

主要思路：每次记录下未排序中的元素的最小（大）元素的索引，然后和已排序的数组的后面的元素交换
特点：不稳定排序（从上面的例子看，第一个5到了第二个5的后面），不需要额外的内存

代码：

def SelectionSort(alist):
    for i in range(len(alist)):
        min_index = i
        for j in range(i + 1, len(alist)):
            if alist[j] < alist[min_index]:
                min_index = j
        alist[i], alist[min_index] = alist[min_index], alist[i]
    return alist

二. 堆排序

主要思路：首先通过下滤构造最大（小）堆，然后交换根节点和最后一个元素，对前n - 1重新建堆（只需要将新的根节点进行一次下滤即可），直到所有元素排序完成。

考虑堆是一颗完全二叉树，如果我们用数组存储每个结点的值，那么假设父节点的索引为i，其左儿子的索引为2 * i + 1，右儿子的索引为 2 * i + 2。假设构建最小堆，在下滤过程中，父节点需要和较小的儿子比较，如果它的值大于儿子的值，则需要将儿子的值上移，它则继续和接下来的儿子比较直到它的值大于儿子的值

heapsort

def percDown(alist, root, n):
    """
    在范围[root:n]的范围内，对root结点进行下滤
    """
    len_list = len(alist)
    father = root
    child = root * 2 + 1
    while child < n:
        if child + 1 < n and alist[child] > alist[child + 1]:  # 找出较小的子节点
            child += 1
        if alist[father] > alist[child]:  # 如果父节点大于子节点则交换
            alist[father], alist[child] = alist[child], alist[father]
        else: break  # 如果父节点小于子节点则直接退出
        father = child
        child = father * 2 + 1
    return alist

特点：不稳定排序（上面的例子看得到，第一个5到第二个5后面了），不需要额外的内存

代码：

def HeapSort(alist):
    alist = buildHeap(alist)
    for i in range(len(alist) - 1, -1, -1):
        alist[0], alist[i] = alist[i], alist[0]
        percDown(alist, 0, i)
    return alist


def buildHeap(alist):
    """
    构建最小堆
    """
    # 从最后一个有子结点的结点开始下滤
    for i in range(int(len(alist) / 2) - 1, -1, -1):
        percDown(alist, i, len(alist))
    return alist


def percDown(alist, root, n):
    len_list = len(alist)
    father = root
    child = root * 2 + 1
    while child < n:
        if child + 1 < n and alist[child] > alist[child + 1]:  # 找出较小的子节点
            child += 1
        if alist[father] > alist[child]:  # 如果父节点大于子节点则交换
            alist[father], alist[child] = alist[child], alist[father]
        else: break  # 如果父节点小于子节点则直接退出
        father = child
        child = father * 2 + 1
    return alist

插入排序

主要思路：对每一个新的元素，都将其插入到已排序好的有序表中，在插入过程中，其后面的元素均向后移动一格
特点：稳定排序，不需要额外内存

代码：

def InsertionSort(alist):
    for i in range(1, len(alist)):
        # 保存当前要插入的元素，并腾出当前空格
        current_index = i
        current_value = alist[i]
        # 和前面的元素比较
        for j in range(i - 1, 0, -1):
            # 如果前面的元素比它大，则将前面的元素向右移一格
            if alist[j] > current_value:
                alist[j + 1] = alist[j]
                current_index = j
            else: break
        # 将当前元素插进空格
        alist[current_index] = current_value
    return alist

归并排序

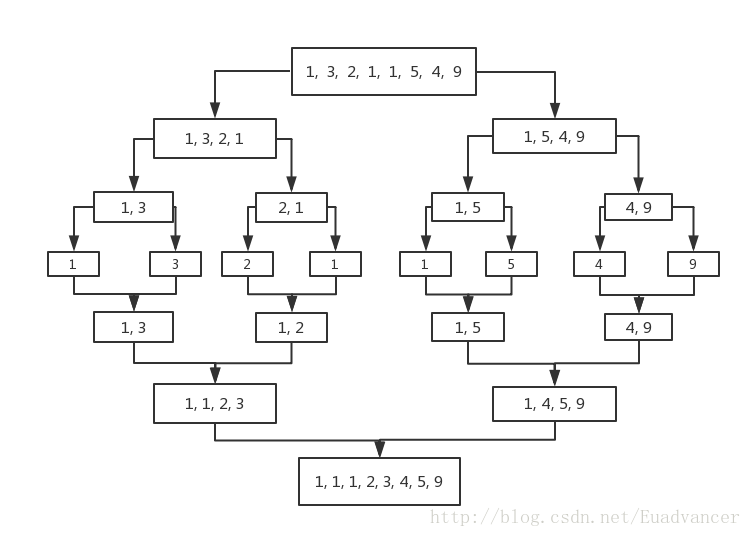
主要思路：归并排序主要利用分治的思想，将待排序的数组分为两部分，如果左边部分已经排序好，右边部分也排序好，那么只需将这两部分再按照顺序组合在一起就可以了
特点： 稳定排序，需要额外的内存（合并操作的时候）

代码：

def MergeSort(alist):
    if len(alist) <= 1: return alist
    middle = int(len(alist) / 2)
    left = MergeSort(alist[:middle])
    right = MergeSort(alist[middle:])
    return merge(left, right)


def merge(left, right):
    left_index = 0
    right_index = 0
    res = []
    while left_index < len(left) and right_index < len(right):
        if left[left_index] < right[right_index]:
            res.append(left[left_index])
            left_index += 1
        else:
            res.append((right[right_index]))
            right_index += 1
    if left_index < len(left):
        res += left[left_index:]
    if right_index < len(right):
        res += right[right_index:]
    return res

计数排序

主要思路：非基于比较的排序算法（因为数组下标索引默认是有顺序的，所以只要将数字对应放进去就会有顺序）。对每一个输入元素x，确定出小于x的元素个数（即它的位置），然后放到输出数组中。在最后遍历的时候一定要从后向前遍历，否则排序将不稳定。
特点：稳定排序，需要额外的内存

代码：

def CountingSort(alist, k):
    temp = [0 for _ in range(k + 1)]  # 存储alist中的每个元素的位置
    res = [0 for _ in alist]  # 保存排序后的结果
    for i in alist:  # temp[i]中存放了值为i的元素的个数
        temp[i] += 1
    for t in range(1, len(temp)):  # temp[i]中存放的是小于等于i元素的数字个数
        temp[t] += temp[t - 1]
    # 把输入数组中的元素放在输出数组中对应的位置上
    for i in range(len(alist) - 1, -1, -1):  # 从后向前输出，保证重复元素按原顺序输出
        res[temp[alist[i]] - 1] = alist[i]  # temp[alist[i]]代表alist的第i个元素的位置
        temp[alist[i]] -= 1  # 确保当遇到重复的数字时，输出相应的位置
    return res

基数排序

主要思路：基数排序分别从每一位开始排序（先从个位，然后十位，百位 …），比如12， 34， 7，首先按照个位排序得到12， 34， 7，然后按照十位排序（7的十位为0），得到7， 12， 34。它对于每一位的排序就是使用计数排序，因为每一位的范围只在0-9，且计数排序是稳定排序，所以基数排序也是稳定排序
特点：稳定排序， 需要额外的内存（因为计数排序就需要额外的内存）

代码：

def RadixSort(alist, d):
    for i in range(1, d + 1):
        alist = CountingSort(alist, 9, i)  # 每次以第i位排序，因为计数排序是稳定的，所以可以多次排序
    return alist


def CountingSort(alist, k, d):
    temp = [0] * (k + 1)
    res = [0] * len(alist)
    for a in alist:
        a = getBitData(a, d)  # 得到第d位数字
        temp[a] += 1
    for i in range(1, len(temp)):
        temp[i] += temp[i - 1]
    for i in range(len(alist) - 1, -1, -1):
        a = getBitData(alist[i], d)
        res[temp[a] - 1] = alist[i]
        temp[a] -= 1
    return res


def getBitData(e, d):
    """
    得到第d位数字
    :param e:
    :param d:
    :return:
    """
    res = e
    for _ in range(d):
        res = e % 10
        e //= 10
    return res