线性分类器其实我已经接触不少了,不同于KNN,它涉及到了更多的知识,比如cost function, objective function等,svm涉及到的知识确实比较多且难理解,但当我们得到相应公式后其实实现起来并不算繁琐,相反很容易理解
线性SVM
目标函数
目标函数我们在以前的线性回归,逻辑回归中都见到过
代价函数
SVM的代价函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值delta, 所以它的代价函数如下:
即在确定正确分类的分数(scores[y[i]])后,其他分类上的分数都要减去它并且加上一个边界值 ( scores[y[!i] - screos[y[i]] + delta ),当得到的值小于0时则代表正确分类比不正确分类高出了一个边界值,否则则要计算损失值。 比如,假设有3个分类,并且得到了分值[13, -7, 11], 第一个分类为正确分类,delta为10,那么根据代价函数,我们可以得到以下算式
以上代价函数计算公式称为折叶损失(hinge loss),当然除此之外还有平方折叶损失SVM(即L2-SVM),就是加个平方,我们可以通过交叉验证或者验证集来确定到底选用哪个
正则项
在ML中,过拟合问题一直是影响模型准确率的重大因素,所以我们还要加上L2范式正则项(在这里,正则项还确保了SVM有最大边界(max margin)等好处),所以最终我们得到以下整个代价函数公式
梯度计算
在训练过程中,我们需要通过最优化方法来是代价函数的损失值达到尽可能的小,所以我们对代价函数进行微分,然后计算其偏导数,得到以下公式
对于每一个训练样本,我们计算它在每个分类上的得分,每当它在某一分类产生了损失(即scores[y[!i] - screos[y[i]] + delta > 0),那么我们就将该分类上的参数梯度+Xi
同时正确分类(y[i])的参数梯度-Xi
再简单的说就是,对于每个Xi,每一个会产生损失值的分类(scores[y[!i] - screos[y[i]] + delta > 0)都会将其参数梯度+Xi,同时在正确分类(y[i])上的梯度-Xi
将以上的公式转化成代码,用非向量化实现(更容易理解)如下








 本文详细介绍了如何使用线性SVM对CIFAR10数据集进行分类。从目标函数、代价函数(包含正则项和折叶损失)、梯度计算到模型的训练和预测函数,逐一深入讲解。最后通过自动化确定超参数并训练模型,得到测试集准确率约为37%。
本文详细介绍了如何使用线性SVM对CIFAR10数据集进行分类。从目标函数、代价函数(包含正则项和折叶损失)、梯度计算到模型的训练和预测函数,逐一深入讲解。最后通过自动化确定超参数并训练模型,得到测试集准确率约为37%。
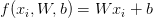
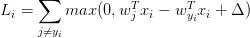
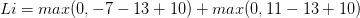
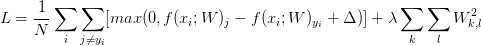
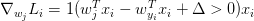
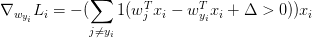
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 1636
1636

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








