WQS二分

本博客以一种较为少见的方式来解释WQS二分。

题目

首先，WQS二分用于解决什么问题？

我们先看一个伞兵题目：

有一个 $n$ 个数的数组 $a$。
求在 $a$ 中恰好选择 $m$ 个数的情况下，选择的数的和的最大值。

你现在看到了这个题目，你发现你不会排序，不会贪心。好难啊，你想。

你打算用另一种方式解决这题。

做法

我们定义 $g(x)$ 为恰好选择 $x$ 个数的情况下，选择的数的和的最大值。

经过观察，我们发现 $g(x)$ 是一个凸函数。

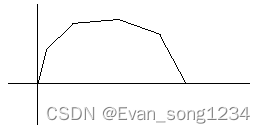
这表明，$g(x)$ 只有一个最大值（也就是把所有正数都取了的情况）。

但你取不到，因为他不一定是 $m$。

如果我们不考虑 $m$ 的限制，肯定会取这个最大值。

那么我们考虑如何做出改变使得不用考虑 $m$ 的限制。

考虑给选择数一个惩罚或奖励 $k$，我们每次选择一个数，答案就增加 $k$。（谁告诉你 $k$ 不能是负数了）

于是，这个函数 $g(x)$ 就转变成另一个函数 $f(x)=g(x)+kx$ 了。

显然，当 $k$ 取值增大，$f(x)$ 的最大值取值位置就往右移动。当 $k$ 取值减少，$f(x)$ 最大值取值位置往左移动。

而我们能够轻而易举的对于每个 $k$ 计算 $f(x)$ 最大值取值位置和 $f(x)$ 最大值（$O(n)$）。

• 由于 $f(x)$ 是选择 $x$ 个时的最大值，那么 $f(x)$ 的最大值就是选择任意个的最大值，相当于取消了最大值限制。

所以，我们可以二分 $k$，根据当前 $k$ 下 $f(x)$ 最大值取值位置与题目限制 $m$ 的大小关系来更改 $k$。

最终可以获得最大值取值位置为 $m$ 时的 $k$ 和 $f(m)$。

然后通过 $f(x)=g(x)+kx$，可以反推出 $g(m)=f(m)-km$。

做完了，$O(n\log n)$。我们震惊的发现时间复杂度和原做法没区别。

好，想必到这里你大致看懂WQS二分的用法或者大致知道WQS二分时什么东西了。

为了方便理解，我们再来一道题（一道需要用到WQS二分的题目）。

题目

有一张 $n$ 个点，$m$ 条带权边的图 $G$，每条边权值为 $w_i$。
求图 $G$ 的生成树的最大权值和，满足点 $s$ 恰好选择 $t$ 条边。

首先发现本题难以使用 $dp$ 之类算法来做。

其次，本题取消限制后极其容易。

最后，容易发现 ，关于 $t$ 的函数 $g(t)$ 代表选择 $t$ 条时的答案，是一个凸函数。

我们就可以使用WPS二分以 $O(\log n)$ 的代价换取取消限制。

做法

还是一样，我们取消限制，然后增加奖励或惩罚 $k$。

根据取最大值位置与 $t$ 的关系，二分惩罚 $k$，直接使用最小生成树 $O(n)$ 来计算惩罚为 $k$ 时最大值。

最终可以得出在一定惩罚下，取 $m$ 条边时的最大值。我们只需要减去惩罚即可。

也可以换一种方法理解。

我们将 $g(x)$ 的图像画出，是一个凸函数。

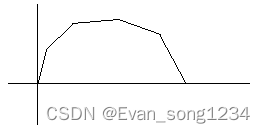
我们现在需要求 $x=t$ 时的取值 $g(t)$。

我们发现对于每个在 $g(x)$ 上的点 $(x,g(x))$，都存在一个斜率 $k$，使得经过这个点的斜率为 $k$ 的直线 $l$ 能与 $g(x)$ 相切。

因为 $g(x)$ 是一个凸函数，所以随着 $x$ 的增大，$(x,g(x))$ 对应斜率 $k$ 会随之增大。

所以我们可以通过二分斜率 $k$，来求出 $x=t$ 时的取值 $g(t)$。

对于每次二分的斜率 $k$，我们要求 $g(x)$ 中切线斜率为 $k$ 的切点。我们设直线 $l$ 的 $y$ 轴截距为 $f(x)$，代表斜率为 $k$ 的直线 $l$ 经过点 $(x,g(x))$ 时的 $y$ 轴截距。

则 $g(x)=kx+f(x)$。

容易发现，当 $f(x)$ 取到最大值时，$y=kx+f(x)$ 就会与 $g(x)$ 函数相切，切点则是此时的 $(x,g(x))$

所以我们尝试求出 $f(x)$ 最大值，从 $g(x)=kx+f(x)$ 可得 $f(x)=g(x)-kx$。

这个式子可以感性理解为：$f(x)$ 为将与 $s$ 相连的边中所选的 $x$ 条边的权值都减少 $k$ 时，选择 $x$ 条边时的生成树的最大权值和。

所以 $f(x)$ 中最大值则为：将与 $s$ 相连的边中所选的边的权值都减少 $k$ 时，最大生成树的权值和。

所以我们可以非常容易的求出 $f(x)$ 最大值，和取得最大值时选择的边数 $x$。

我们就可以开始二分了。

对于最终求出的 $f(t)$，我们可以根据 $g(x)=kx+f(x)$，求出 $g(t)$。

总结

经过上面几题可以发现，WQS二分适用于符合一下几点的问题：

• 有一个恰好选择的个数限制 $m$
• 代表恰选 $x$ 个时答案的函数 $g(x)$ 需要为凸函数。
• 取消限制 $k$ 后问题可以快速计算。

解决时，一般选取一个附值 $k$，使得每多选一次，最终答案就增加 $k$。然后计算当附值为 $k$ 时的最大值取值位置 $x_0$。将其与限制 $m$ 像比较。由于函数是凸函数，附值为 $k$ 时的取最大值位置 $h(k)=x_0$ 有单调性。所以可以二分 $k$ 让 $x_0$ 靠近 $m$，最终计算得当附值为 $k_0$ 是取最大值位置 $h(k_0)=m$ 时。再将附值为 $k_0$ 时的最大值减去 $k\times m$ 即可。