论文：Unfolded Deep Neural Network(UDNN) for High Mob

已于 2022-10-05 19:18:14 修改
阅读量396 收藏 1
点赞数 1
CC 4.0 BY-SA版权
分类专栏： 无线信道 文章标签： 深度学习 人工智能 机器学习
于 2022-09-14 19:01:57 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/FDS99999/article/details/126818950
UDNN是一种深度学习网络，它模仿ISTA（迭代 shrinkage-thresholding 算法）来解决压缩感知问题。网络设计包含两条并行线处理实部和虚部，所有参数如非线性变换、收缩阈值等通过反向传播学习。UDNN将ISTA的迭代步骤转化为深度学习层，以低计算复杂度解决LASSO问题，保留了ISTA的结构并引入了可学习的非线性变换和重构层。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

UDNN：通过将ISTA（Iterative shrinkage-thresholding algorithm）求解器映射到深度学习网络来解决压缩感知问题。

在UDNN网络中设计了两条平行线，分别用于实部和虚部的计算，这些线中的信息相互交错，以保证网络运算等价于复杂运算。此外，UDNN包含两个重复阶段，分别对应于ISTA中的两个迭代步骤。

不同于传统的线性变换，UDNN采用了非线性可学习和稀疏变换，UDNN中涉及的所有参数(如非线性变换、收缩阈值、测量矩阵等)都是通过反向传播端到端学习的。

LASSO公式可用于估计矢量化的高速信道x:  \underset{x}{min}\frac{1}{2}\left \| y-Ax \right \|_{2}^{2}+\lambda \left \| x \right \|_{1}

 ISTA解决上面的问题需要使用以下两个迭代步骤：:

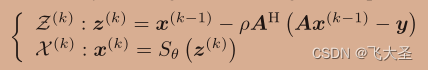
提出的UDNN以低计算复杂度求解这个LASSO问题

UDNN的基本思想是充分利用ISTA方法的优点，对以前的ISTA迭代进行映射到一个由固定数量的层组成的深度神经网络，每一层对应ISTA中的一次迭代。

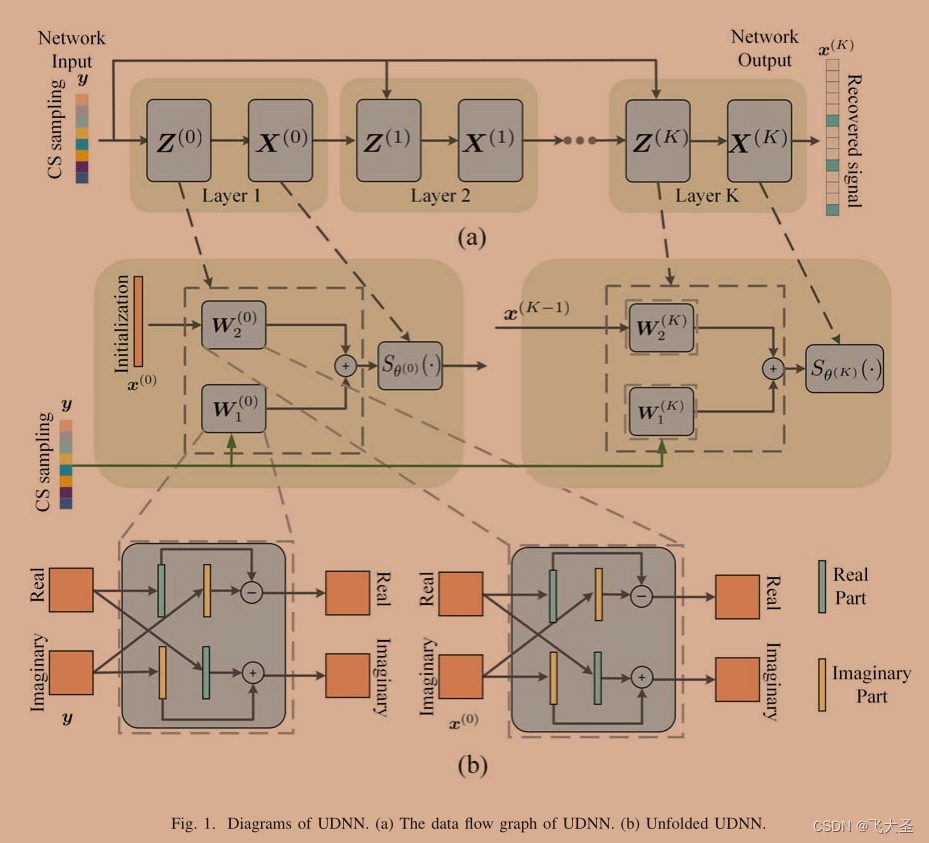
  •  ISTA的第k次迭代对应于的第k层
  • 箭头对应操作之间的数据流
  • 每一层中，两类节点分别映射定义的非线性变换操作和重构操作
  • 在网络中使用两条平行传播线分别计算实部和虚部，两条传播线之间进行信息交换，以确保网络中的运算等价于复杂运算，而只使用实数

深度UDNN保留了ISTA的结构，但将两个操作(Z (k)， X (k))归纳为两个可学习层，即重构层和非线性变换层

DNN（全连接神经网络）
m0_63167598的博客
03-16 3万+
一. DNN网络一般拥有三层 1.输入层 2.隐藏层 3.输出层 简单网络如下： 二.正向传播 从第二层开始，每一个神经元都会获得它上一层所有神经元的结果。即每一个 y = wx + b的值。 具体分析如下： 如此下去就会非常可能出现了一个问题------就是越靠后的神经元获得的y值会非常大，试想一下，如果这个数远远大于它前面神经元的值，前面神经元对整个网络的表达就显得毫无意义。所以我们在每创建一层网络时就要多“y”进行一次约束。 我们有很多选择，但最好的方法就是运用Sig...
U-Net网络
daguantou的博客
07-30 1万+
U-Net在架构设计和其他利用卷积神经网络基于像素的图像分割方面更成功，对有限数据集的图像更有效。此次项目中，去除池化层和增加跳跃连接是一个很好的选择。池化层会丢失图像信息和降低图像分辨率且是不可逆的操作，对图像分割任务有一些影响。...
GPU、CUDA和cuDNN分别是什么，之间又有什么关系？
eastking0530的博客
08-28 4084
GPU、CUDA和cuDNN分别是什么，之间又有什么关系？
U-Net网络结构详解
AKxiaokui的博客
05-30 1万+
U-Net网络结构详解 U-Net网络结构是对称的，由于网络结构像U型，所以被命名为U-Net。整体而言，U-Net是一个Encoder-Decoder（编码器-解码器）的结构，这一点是与FCN的结构相同。 该网络结构的左半部分是特征提取，右半部分是上采样。Encoder是由卷积和下采样组成，所用的卷积结构统一为33的卷积核，Unet的卷积都是valid卷积（而非same），这么做是为了，网络只使用输入图片的信息。如果会用same卷积，这样每次3x3卷积就不会改变特征图的尺寸了，最终上采样回来的尺寸就能够
论文--阅读翻译笔记-Reducing the Dimensionality of Data with Neural Networks
塞北战斗民族的博客
06-05 4566
摘要：通过训练小中间层（small central layer）的多层神经网络（神经元个数小于维数），可以将高维数据（high-dimensional data）转换为低维编码（low-dimensional codes），以此（通过此网络）来重建（reconstruct ）高维输入向量（high-dimensional input vectors）。其中这个神经网络的中间层神经元数是较少的，可把...
【无线通信领域】基于深度学习的多用户MIMO检测算法DeepSIC：非线性信道与CSI不确定性下的软干扰消除系统设计 （复现论文或解答问题，含详细可运行代码及解释）
04-05
内容概要：论文《DeepSIC: Deep Soft Interference Cancellation for Multiuser MIMO Detection》提出了一种基于深度学习的多用户MIMO检测方法DeepSIC。传统干扰消除算法依赖线性信道模型和精确的信道内容概要：论文...
《Involution：Inverting the Inherence of Convolution for Visual Recognition》论文笔记
m_buddy的博客
07-19 832
参考代码：involution 1. 概述 导读：CNN操作已经被广泛使CV领域，其具有空间无关性（spatial-agnostic）和通道特异性（channel-specific），前一个性质来源于在空间尺度上共享卷积参数，后一个性质来自于输出通道维度上的参数各不相同。在这篇文章中提出了一种性质与之相反的操作involution，通过学习的方式去得到卷积参数，之后经过维度变换之后与unfold之后的特征进行multiply-add，从而得到最后的输出结果，这里用到的multiply-add操作可以看作是
Introduction to Graph Neural Network (GNN) 图神经网络入门详解
Jay_Tang的博客
08-17 3877
文章目录往期文章链接目录NoteBackground and IntuitionIntro to Graph Neural NetworksGNNs FrameworkDefinitionRecurrent graph neural networks (RecGNNs)Introduction to RecGNNsBanach's Fixed Point TheoremRecGNNs v.s. RNNsLimitation of RecGNNsGated Graph Neural Networks (GGN
RuntimeError: "unfolded2d_copy" not implemented for 'Half'
04-25
这个错误是因为您尝试使用 PyTorch 的 unfold 操作符时，输入张量的 dtype 为“Half”，但是未实现“unfolded2d_copy”操作符的该 dtype 版本。您需要将输入张量的 dtype 更改为支持 unfold 操作符的 dtype，例如...
runtimeerror: "unfolded2d_copy" not implemented for 'half'
06-28
这个错误通常出现在使用PyTorch时。它意味着你正在尝试在数据类型为“half”的张量上执行某个操作，而该操作还没有被实现。"half"类型通常是指16位浮点数，它比32位的浮点数（float）占用更少的内存，但在一些操作中...
一行命令解决 ubuntu libcudnn.so.5 不是符号连接
01-28 4451
usr/local/cuda-8.0/lib64/libcudnn.so.5不是符号连接的问题，解决办法也很简单，重新建立链接并删除原链接 ln -sf /usr/local/cuda-8.0/lib64/libcudnn.so.5.0.5 /usr/local/cuda-8.0/lib64/libcudnn.so.5
错误：/usr/local/cuda-9.0/targets/x86_64-linux/lib/libcudnn.so.7 is not a symbolic link解决方法
阿耀的博客
10-29 7980
错误/sbin/ldconfig.real: /usr/local/cuda-9.0/targets/x86_64-linux/lib/libcudnn.so.7 is not a symbolic link的原因及解决方法。 在Ubuntu18.04下配置Caffe-GPU时候，运行以下代码出现libcudnn.so.7 is not a symbolic link的错误. sudo apt ...
Windows10安装 cuDNN 方法
CatOneTwo的专栏
05-24 2万+
安装好 CUDA 后安装 cudnn 下载地址：cuDNN Download 需要注册信息，然后找CUDA对应的版本下载，所以要记住自己是哪个版本，我是10.1就选择第一项。 下载下来是个压缩包，解压后，里面有三个文件夹。 找到 CUDA 的安装路径，我的是 C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v10.1 配置： 复制 cuD...
Ubuntu安装CUDA和cuDNN
imbabao的博客
08-06 1122
我的环境 Ubuntu16.04_x64 CUDA_9.2 uDNN_7.1.4 一、安装CUDA 1.进入官网，根据自己的系统选择版本开始下载 链接 2.下载完成后进入目录，按照官网给定的四条命令进行安装 sudo dpkg -i cuda-repo-ubuntu1604-9-2-local_9.2.148-1_amd64.deb sudo apt-key add /var...
libcudnn.so.7 is not a symbolic link
七爷OK
08-03 1万+
安装 libnccl2 的时候： apt-get install libnccl2=2.2.13-1+cuda9.0 libnccl-dev=2.2.13-1+cuda9.0 中途显示了一个错误： Reading package lists... Done Building dependency tree Reading state information... Done ...
cuDNN的安装（版本选择， Runtime 还是 Developer）
热门推荐
Keeplearning
11-29 3万+
cuDNN的版本选择： Runtime 还是 Developer ? 在安装完CUDA之后，一般都要安装cuDNN，但是很多教程上都只说到了具体的安装步骤，到底如何下、下载哪一个版本的都没有讲，比如我在安装完 CUDA10.1 之后，要安装 cuDNN7.6 ，到了官网下载时候就不知道该具体选择哪一个，在这里记录一下。 一、CUDA 和 cuDNN 的对应版本 参考官网链接： https://d...
Iterative Algorithm Induced Deep-Unfolding Neural NetworksPrecoding Design for MultiuserMIMOSystem 1
xd1501013的博客
12-25 799
1.Abstract Abstract—Optimization theory assisted algorithms have received great attention for precoding design in multiuser multiple-input multiple output (MU-MIMO) systems. Although the resultant optimization algorithms are able to provide excellent perfo
【转】Understanding LSTM
luchi007的专栏
04-12 347
Recurrent Neural Networks Humans don’t start their thinking from scratch every second. As you read this essay, you understand each word based on your understanding of previous words. You don’t throw...
循环神经网络 中文情感分析案例
最新发布
2301_76654710的博客
07-28 859
目录一、数据处理1、读取原始文件2、清洗数据3、分词4、构建词典并保存5、把每条文本编码成数字列表6、固定长度二、设置数据集、数据加载器三、构建模型结构四、配置具体模型参数与训练细节五、开始训练并保存六、模型测试（测试集）七、单条评论测试（可选）又做了一个小案例，刚好来复盘一下，是关于分析酒店评论的好坏，首先原始数据集如下：前面一列是标签，1代表好评，0代表差评，后面的是评论内容，一共有5000多条评论，下面开始：这里我总结了一下大概的步骤：读取原始文件 --> 清洗数据（去除标点符号等） --> 分词 -
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

飞大圣

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值