【MATLAB】【公式验证】泰勒级数

最新推荐文章于 2024-12-20 10:04:59 发布

学不会又咋了

最新推荐文章于 2024-12-20 10:04:59 发布

阅读量3.5k

点赞数 7

分类专栏：基于MATLAB的数学公式验证文章标签： matlab

本文链接：https://blog.csdn.net/FORWARDGOOD/article/details/124165747

版权

基于MATLAB的数学公式验证专栏收录该内容

2 篇文章

订阅专栏

本文通过MATLAB演示了泰勒级数在指数函数和三角函数上的拟合效果，展示随着项数增加如何提高拟合精度。分析表明，在特定区间内，适当增加项数能有效逼近原函数。例如，指数函数在(0,5)区间用十项即可深度拟合，而三角函数在(-π,π)区间用四项达到深度拟合。但随着区间扩大，需增加项数以保持拟合质量。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

泰勒级数

关于泰勒级数的概念和工程意义在这不再叙述，此文章只是用matlab把图形拟合出来，让读者形象地感受随着项数的增加，函数拟合效果逐渐逼近。
常见的函数泰勒展开：
请添加图片描述

指数函数

三项拟合效果：

x=0:0.01:5;
y1=exp(x);
y2=1+x+1/factorial(2)*power(x,2)+1/factorial(3)*power(x,3);
plot(x,y1,x,y2);
xlabel('x')
ylabel('y')

在这里插入图片描述
五项拟合效果：

x=0:0.01:5;
y1=exp(x);
y2=1+x+1/factorial(2)*power(x,2)+1/factorial(3)*power(x,3)+1/factorial(4)*power(x,4)+1/factorial(5)*power(x,5);
plot(x,y1,x,y2);
xlabel('x')
ylabel('y')

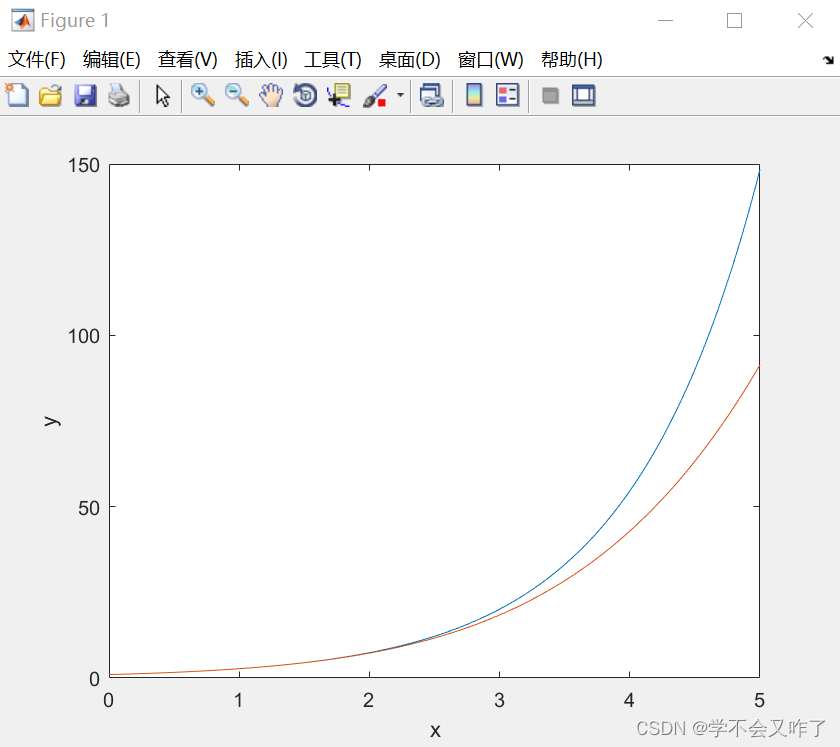
在这里插入图片描述
十项拟合效果：

x=0:0.01:5;
y1=exp(x);
y2=1+x+1/factorial(2)*power(x,2)+1/factorial(3)*power(x,3)+1/factorial(4)*power(x,4)+1/factorial(5)*power(x,5)+1/factorial(6)*power(x,6)+1/factorial(7)*power(x,7)+1/factorial(8)*power(x,8)+1/factorial(9)*power(x,9)+1/factorial(10)*power(x,10);
plot(x,y1,x,y2);
xlabel('x')
ylabel('y')

在这里插入图片描述
以上分析，当有十项时，在（0，5）区间上已经深度拟合了，但是随着区间的增加，必须要增加项数才能“跟得上”原函数的变化。
例如区间增大到10：

x=0:0.01:10;
y1=exp(x);
y2=1+x+1/factorial(2)*power(x,2)+1/factorial(3)*power(x,3)+1/factorial(4)*power(x,4)+1/factorial(5)*power(x,5)+1/factorial(6)*power(x,6)+1/factorial(7)*power(x,7)+1/factorial(8)*power(x,8)+1/factorial(9)*power(x,9)+1/factorial(10)*power(x,10);
plot(x,y1,x,y2);
xlabel('x')
ylabel('y')

在这里插入图片描述

三角函数

二项拟合：

x=-pi:0.01:pi;
y1=sin(x);
y2=x-power(x,3)/factorial(3);
plot(x,y1,x,y2);
xlabel('x')
ylabel('y')

在这里插入图片描述
三项拟合：

x=-pi:0.01:pi;
y1=sin(x);
y2=x-power(x,3)/factorial(3)+power(x,5)/factorial(5);
plot(x,y1,x,y2);
xlabel('x')
ylabel('y')

在这里插入图片描述
四项拟合：

x=-pi:0.01:pi;
y1=sin(x);
y2=x-power(x,3)/factorial(3)+power(x,5)/factorial(5)-power(x,7)/factorial(7);
plot(x,y1,x,y2);
xlabel('x')
ylabel('y')

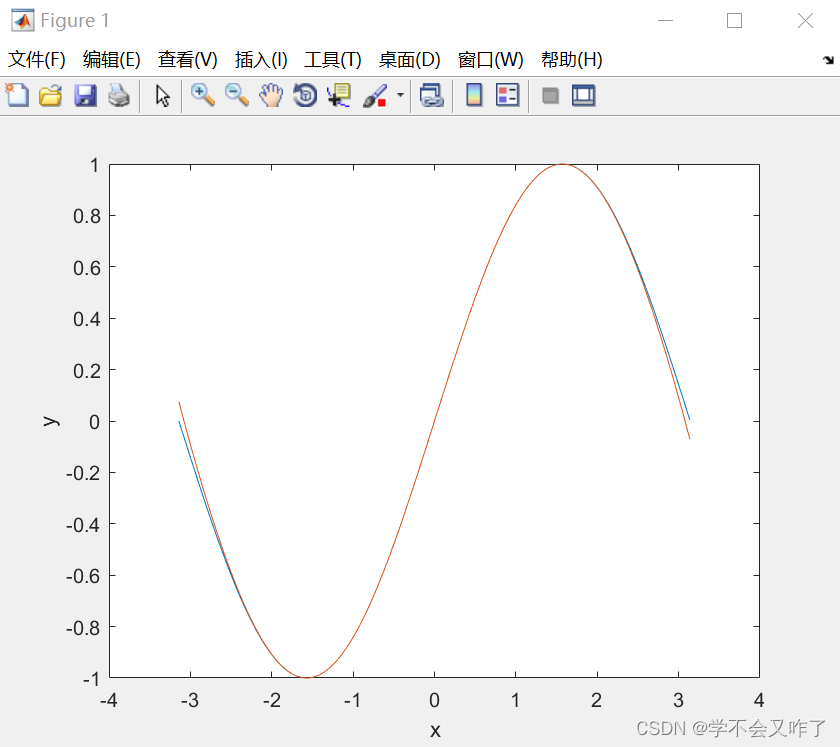
在这里插入图片描述
以上分析，当有四项时，在（-pi，pi）区间上已经深度拟合了，但是随着区间的增加，必须要增加项数才能“跟得上”原函数的变化。
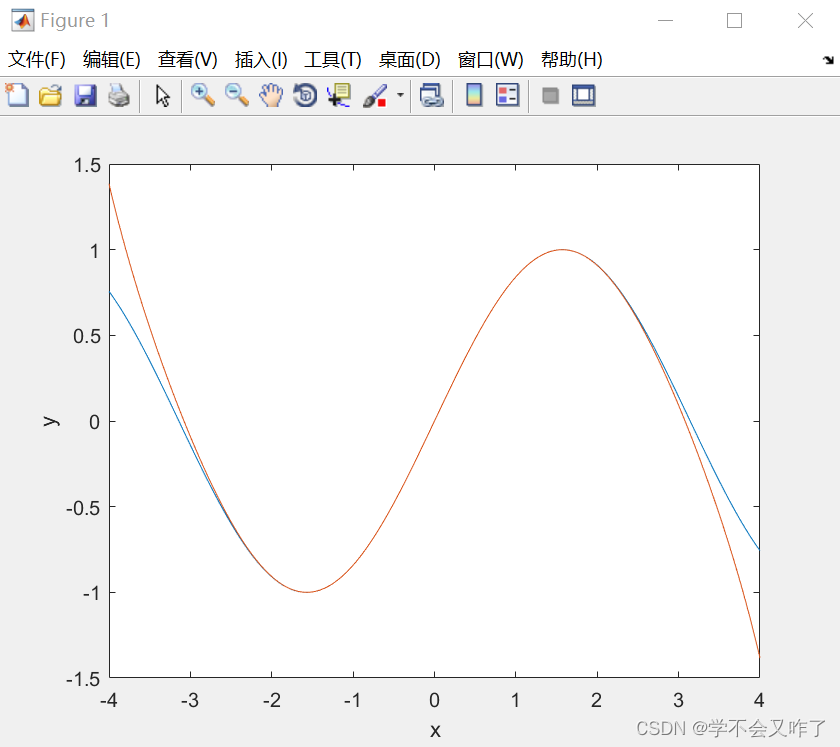
例如区间增大到（-4，4）：

x=-4:0.01:4;
y1=sin(x);
y2=x-power(x,3)/factorial(3)+power(x,5)/factorial(5)-power(x,7)/factorial(7);
plot(x,y1,x,y2);
xlabel('x')
ylabel('y')

在这里插入图片描述

总结

数学是如此的奇妙！