C++中的树、二叉树、二叉树遍历、二叉树前序、中序、后序遍历相互求法

本博文来总结下树、二叉树以及二叉树前序、中序、后序遍历相互求法，即如果知道两个的遍历，如何求第三种遍历方法，比较笨的方法是画出来二叉树，然后根据各种遍历不同的特性来求，也可以编程求出，下面我们分别说明。

1、什么是树？什么是二叉树？

树是一种数据结构，它是由n（n>=1）个有限结点组成一个具有层次关系的集合。

二叉树是指结点的度不超过2的有序树。

（结点的度：树中的一个结点拥有的子树数目。）

2、二叉树的前序、中序、后序遍历的特性 

二叉树前序遍历特性：

 
（1）、访问根节点 

（2）、前序遍历左子树 

（3）、前序遍历右子树 


二叉树中序遍历特性： 

（1）、中序遍历左子树 

（2）、访问根节点 

（3）、中序遍历右子树 

二叉树后序遍历特性：

 
（1）、后序遍历左子树 

（2）、后序遍历右子树 

（3）、访问根节点

3、已知前序、中序遍历，求后序遍历

例：

前序遍历:         GDAFEMHZ

中序遍历:         ADEFGHMZ

3.1、画树求法

第一步、根据前序遍历的特点，我们知道根结点为G

第二步、观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树，G右侧的HMZ必然是root的右子树。

 第三步、观察左子树ADEF，左子树的中的根节点必然是大树的root的leftchild。在前序遍历中，大树的root的leftchild位于root之后，所以左子树的根节点为D。

第四步、同样的道理，root的右子树节点HMZ中的根节点也可以通过前序遍历求得。在前序遍历中，一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树，并且遍历的左子树的第一个节点就是左子树的根节点。同理，遍历的右子树的第一个节点就是右子树的根节点。

第五步、观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了。

该步递归的过程可以简洁表达如下：

1 、确定根，确定左子树，确定右子树。

2 、在左子树中递归。

3 、在右子树中递归。

4 、打印当前根。

那么，我们可以画出这个二叉树的形状：

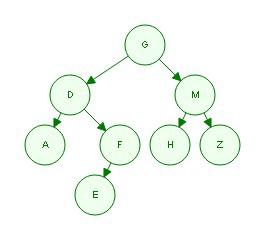
那么，根据后序的遍历规则，我们可以知道，后序遍历顺序为：AEFDHZMG

3.2、编程求法

示例代码如下。

/***************************************************************************/
				/*已知前序、中序遍历，求后序遍历*/
/***************************************************************************/

#include <iostream>  
#include <fstream>  
#include <string>  

using namespace std;

struct TreeNode
{
	struct TreeNode* left;
	struct TreeNode* right;
	char  elem;
};

void BinaryTreeFromOrderings(char* inorder, char* preorder, int length)
{
	if(length == 0)
		{
			//cout<<"invalid length";
			return;
		}
	TreeNode* node = new TreeNode;//Noice that [new] should be written out.
	node->elem = *preorder;
	int rootIndex = 0;
	for(;rootIndex < length; rootIndex++)
	{
		if(inorder[rootIndex] == *preorder)
		break;
	}
	//Left
	BinaryTreeFromOrderings(inorder, preorder +1, rootIndex);
	//Right
	BinaryTreeFromOrderings(inorder + rootIndex + 1, preorder + rootIndex + 1, length - (rootIndex + 1));
	cout<<node->elem;
	return;
}
 
int main(int argc, char* argv[])
{
	printf("Question: 已知前序、中序遍历，求后序遍历\n\n");

	char* pr="GDAFEMHZ";//前序
	char* in="ADEFGHMZ";//中序


	cout<<"前序是："<<pr<<endl;
	cout<<"中序是："<<in<<endl<<endl;
	cout<<"后序是：";

	BinaryTreeFromOrderings(in, pr, 8);
	printf("\n\n");
	return 0;
}

4、已知中序和后序遍历，求前序遍历

依然是上面的题，这次我们只给出中序和后序遍历：

中序遍历:       ADEFGHMZ

后序遍历:     AEFDHZMG

4.1、画树求法

第一步、根据后序遍历的特点，我们知道后序遍历最后一个结点即为根结点，即根结点为G。

第二步、观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树，G右侧的HMZ必然是root的右子树。

第三步、观察左子树ADEF，左子树的中的根节点必然是大树的root的leftchild。在前序遍历中，大树的root的leftchild位于root之后，所以左子树的根节点为D。

第四步、同样的道理，root的右子树节点HMZ中的根节点也可以通过前序遍历求得。在前后序遍历中，一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树，并且遍历的左子树的第一个节点就是左子树的根节点。同理，遍历的右子树的第一个节点就是右子树的根节点。

第五步、观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了。该步递归的过程可以简洁表达如下：

1、 确定根，确定左子树，确定右子树。

2 、在左子树中递归。

3 、在右子树中递归。

4 、打印当前根。

这样，我们就可以画出二叉树的形状，如上图所示，这里就不再赘述。

那么，前序遍历:         GDAFEMHZ

4.2、编程求法

示例代码如下。

/***************************************************************************/
				/*已知中序、后序遍历，求前序遍历*/
/***************************************************************************/

#include <iostream>
#include <fstream>
#include <string>

using namespace std;

struct TreeNode
{
    struct TreeNode* left;
    struct TreeNode* right;
    char  elem;
};

TreeNode* BinaryTreeFromOrderings(char* inorder, char* aftorder, int length)
{
    if(length == 0)
    {
        return NULL;
    }
    TreeNode* node = new TreeNode;//Noice that [new] should be written out.
    node->elem = *(aftorder+length-1);
    cout<<node->elem;
    int rootIndex = 0;
    for(;rootIndex < length; rootIndex++)//a variation of the loop
    {
        if(inorder[rootIndex] ==  *(aftorder+length-1))
            break;
    }
    node->left = BinaryTreeFromOrderings(inorder, aftorder , rootIndex);
    node->right = BinaryTreeFromOrderings(inorder + rootIndex + 1, aftorder + rootIndex , length - (rootIndex + 1));
    
    return node;
}

int main(int argc, char** argv)
{
    printf("Question: 已知中序、后序遍历，求前序遍历\n\n");
 
    char* in="ADEFGHMZ";	//中序
    char* af="AEFDHZMG";	//后序

    cout<<"中序是："<<in<<endl;
    cout<<"后序是："<<af<<endl<<endl;
    cout<<"前序是：";

    BinaryTreeFromOrderings(in, af, 8); 
    printf("\n\n");
    return 0;
}