数据结构-图
If you can not explain it simply,you do not understand it well enouth!
不能简明的解释一件事,说明你对它懂得不多! --爱因斯坦
一、图的简介
图(Graph)结构是一种非线性的数据结构,图在实际生活中有很多例子,比如交通运输网,地铁网络,社交网络,计算机中的状态执行(自动机)等等都可以抽象成图结构。图结构比树结构复杂的非线性结构。
二、图的基本信息
2.1图结构构成
1.顶点(vertex):图中的数据元素,如图一。
2.边(edge):图中连接这些顶点的线,如图一。
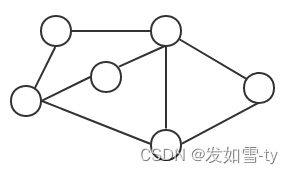
图一
所有的顶点构成一个顶点集合,所有的边构成边的集合,一个完整的图结构就是由顶点集合和边集合组成。图结构在数学上记为以下形式:
G=(V,E) 或者 G=(V(G),E(G))
其中 V(G)表示图结构所有顶点的集合,顶点可以用不同的数字或者字母来表示。E(G)是图结构中所有边的集合,每条边由所连接的两个顶点来表示。
图结构中顶点集合V(G)不能为空,必须包含一个顶点,而图结构边集合可以为空,表示没有边。
2.2图的基本概念
-
1.无向图(undirected graph)
如果一个图结构中,所有的边都没有方向性,那么这种图便称为无向图。典型的无向图,如图二所示。由于无向图中的边没有方向性,这样我们在表示边的时候对两个顶点的顺序没有要求。例如顶点VI和顶点V5之间的边,可以表示为(V2, V6),也可以表示为(V6,V2)。
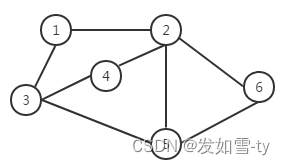
图二 无向图
对于图二无向图,对应的顶点集合和边集合如下:
V(G)= {V1,V2,V3,V4,V5,V6}
E(G)= {(V1,V2),(V1,V3),(V2,V6),(V2,V5),(V2,V4),(V4,V3),(V3,V5),(V5,V6)} -
2.有向图(directed graph)
一个图结构中,边是有方向性的,那么这种图就称为有向图,如图三所示。由于图的边有方向性,我们在表示边的时候对两个顶点的顺序就有要求。我们采用尖括号表示有向边,例如<V2,V6>表示从顶点V2到顶点V6,而<V6,V2>表示顶点V6到顶点V2。
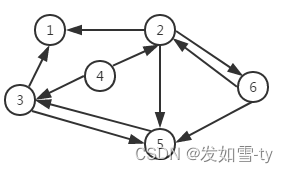
图三 有向图对于图三有向图,对应的顶点集合和边集合如下:
V(G)= {V1,V2,V3,V4,V5,V6}
E(G)= {<V2,V1>,<V3,V1>,<V4,V3>,<V4,V2>,<V3,V5>,<V5,V3>,<V2,V5>,<V6,V5>,<V2,V6>,<V6,V2>}注意:
无向图也可以理解成一个特殊的有向图,就是边互相指向对方节点,A指向B,B又指向A。 -
3.混合图(mixed graph)
一个图结构中,边同时有的是有方向性有的是无方向型的图。
在生活中混合图这种情况比较常见,比如城市道路中有些道路是单向通行,有的是双向通行。
-
4.顶点的度
连接顶点的边的数量称为该顶点的度。顶点的度在有向图和无向图中具有不同的表示。对于无向图,一个顶点V的度比较简单,其是连接该顶点的边的数量,记为D(V)。 例如,图二所示的无向图中,顶点V5的度为3。而V6的度为2。
对于有向图要稍复杂些,根据连接顶点V的边的方向性,一个顶点的度有入度和出度之分。
• 入度是以该顶点为端点的入边数量, 记为ID(V)。
• 出度是以该顶点为端点的出边数量, 记为OD(V)。
这样,有向图中,一个顶点V的总度便是入度和出度之和,即D(V) = ID(V) + OD(V)。例如,图三所示的有向图中,顶点V5的入度为3,出度为1,因此,顶点V5的总度为4。 -
5.邻接顶点
邻接顶点是指图结构中一条边的两个顶点。 邻接顶点在有向图和无向图中具有不同的表示。对于无向图,邻接顶点比较简单。例如,在图二所示的无向图中,顶点V2和顶点V6互为邻接顶点,顶点V2和顶点V5互为邻接顶点等。
对于有向图要稍复杂些,根据连接顶点V的边的方向性,两个顶点分别称为起始顶点(起点或始点)和结束顶点(终点)。有向图的邻接顶点分为两类:
• 入边邻接顶点:连接该顶点的边中的起始顶点。例如,对于组成<V2,V6>这条边的两个顶点,V2是V6的入边邻接顶点。
• 出边邻接顶点:连接该顶点的边中的结束顶点。例如,对于组成<V2,V6>这条边的两个顶点,V6是V2的出边邻接顶点。 -
6.无向完全图
如果在一个无向图中, 每两个顶点之间都存在条边,那么这种图结构称为无向完全图。典型的无向完全图,如图四所示。
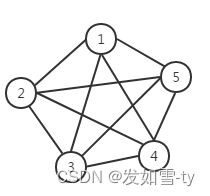
图四 无向完全图
理论上可以证明,对于一个包含M个顶点的无向完全图,其总边数为M(M-1)/2。比如图四总边数就是5(5-1)/ 2 = 10。 -
7.有向完全图
如果在一个有向图中,每两个顶点之间都存在方向相反的两条边,那么这种图结构称为有向完全图。典型的有向完全图,如图五所示。
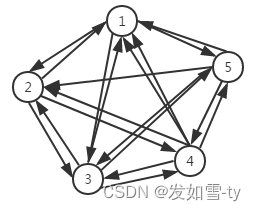
图五 有向完全图
理论上可以证明,对于一个包含N的顶点的有向完全图,其总的边数为N(N-1)。这是无向完全图的两倍,这个也很好理解,因为每两个顶点之间需要两条边。 -
8.有向无环图(DAG图)
如果一个有向图无法从某个顶点出发经过若干条边回到该点,则这个图是一个有向无环图。
有向无环图可以利用在区块链技术中。
- 9.无权图和有权图
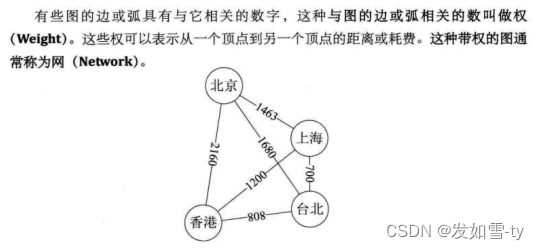
这里的权可以理解成一个数值,就是说节点与节点之间这个边是否有一个数值与它对应,对于无权图来说这个边不需要具体的值。对于有权图节点与节点之间的关系可能需要某个值来表示,比如这个数值能代表两个顶点间的距离,或者从一个顶点到另一个顶点的时间,所以这时候这个边的值就是代表着两个节点之间的关系,这种图被称为有权图;
- 10.图的连通性
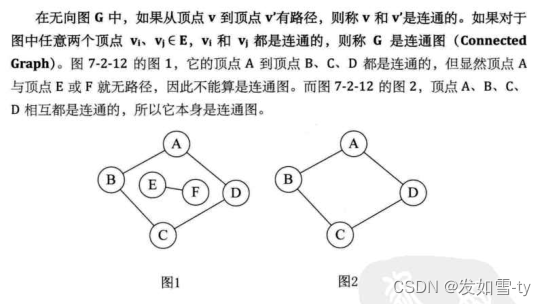
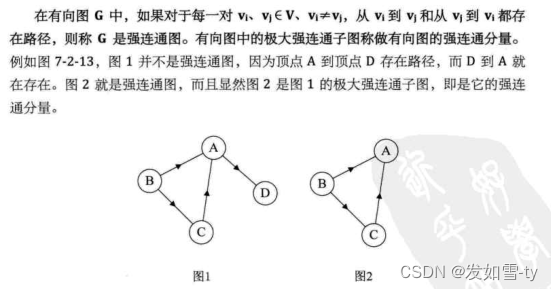
- 11.简单图 ( Simple Graph)
对于节点与节点之间存在两种边,这两种边相对比较特殊
1.自环边(self-loop):节点自身的边,自己指向自己。
2.平行边(parallel-edges):两个节点之间存在多个边相连接。
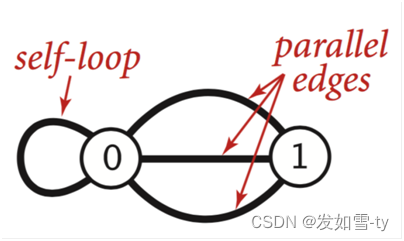
这两种边都是有意义的,比如从A城市到B城市可能不仅仅有一条路,比如有三条路,这样平行边就可以用到这种情况。不过这两种边在算法设计上会加大实现的难度。而简单图就是不考虑这两种边。
三、图的存储
3.1邻接矩阵
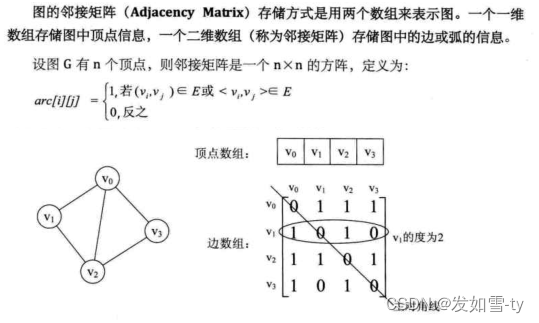
有向图表示:
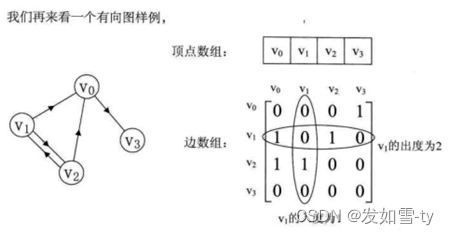
有向网图:
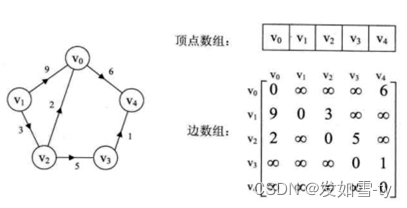
数据结构:
#define NMAXVER 20
//邻接矩阵
struct GraphTag
{
char V[NMAXVER];//顶点
int E[NMAXVER][NMAXVER];//边
int nVCount;//顶点个数
};
3.2邻接表
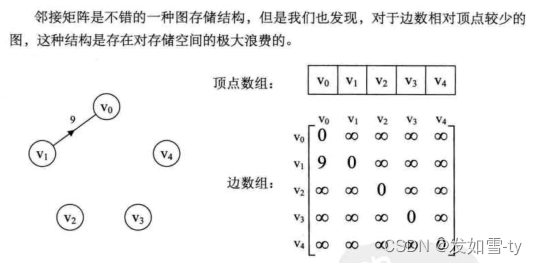
所以前辈们发明了邻接表,如下,无向图的邻接表
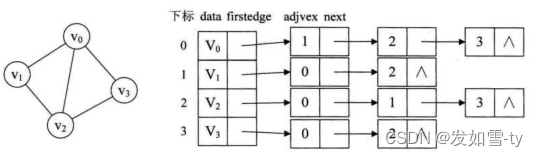
有向图的邻接表:
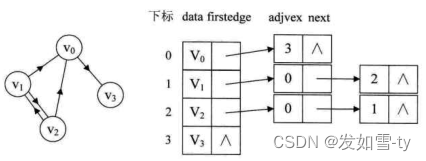
//边表结点
struct EdgeNode
{
int nvex;//存储结点对应的下标
struct EdgeNode* next;//指向下一个邻接点
};
//顶点表结点
struct Vertex
{
char data;//数据
struct EdgeNode *firstEdge;//对应的下标
};
struct GraphList
{
Vertex V[NMAXVER];
int nVCount;//顶点个数
};
四、图的遍历
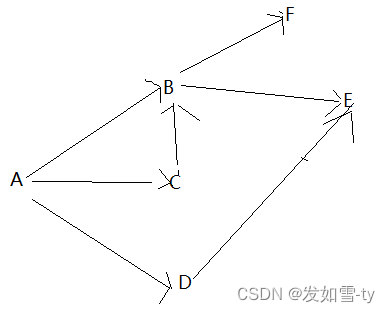

//邻接矩阵
struct MGraph
{
char V[NMAXVER];//顶点
int E[NMAXVER][NMAXVER];//边
int nVCount;//顶点个数
};
//创建一个图
MGraph*CreateGraph(char* Ver, unsigned int nSize)
{
//1.存储顶点
if (nSize <=0)
{
return NULL;
}
//2.创建图与初始化
MGraph* pGraph = new MGraph;//创建一个图
memset(pGraph, 0, sizeof(MGraph));//初始化图
pGraph->nVCount = nSize;
//3.将顶点赋值给刚刚创建的图
for (int i = 0; i < nSize; i++)
{
pGraph->V[i] = Ver[i];
}
return pGraph;
}
//添加一条边
void AddEdge(MGraph* pGraph, int v1, int v2)
{
if (!pGraph) // NULL == pGraph
{
return;
}
if (v1 >= pGraph->nVCount || v2>= pGraph->nVCount)
{
return;
}
pGraph->E[v1][v2] = 1;
}
//打印邻接矩阵
void PrintLinJieArray(MGraph* graph)
{
printf("邻接矩阵:\n");
printf("------------------------\n");
printf(" ");
for (int i = 0; i < graph->nVCount; i++)
{
cout << graph->V[i] << " ";
}
cout << endl;
for (int i = 0; i < graph->nVCount; i++)
{
printf("%c ", graph->V[i]);
for (int j = 0; j < graph->nVCount; j++)
{
printf("%d ", graph->E[i][j]);
}
printf("\n");
}
printf("------------------------\n");
}
4.1 邻接矩阵的深度优先遍历DFS
一条路走到黑,不撞南墙不回头
void DFS(MGraph* pGraph, int v, bool visited[])
{
if (pGraph)
{
printf("%c ", pGraph->V[v]);
visited[v] = true;
}
for (int j = 0;j<pGraph->nVCount;j++)
{
if (pGraph->E[v][j] != 0 && false == visited[j])
{
//对未访问过的邻接顶点递归调用
DFS(pGraph, j, visited);
}
}
}
//深度优先遍历
void MGraph_DFS(MGraph* pGraph)
{
cout << "深度优先遍历:\n";
if (pGraph)
{
bool bArrayVisited[NMAXVER] = { false };//避免重复访问
for (int i = 0;i<pGraph->nVCount;i++)//对未访问过的顶点调用DFS,若为连通图仅仅执行一次
{
if (false == bArrayVisited[i])
{
DFS(pGraph,i,bArrayVisited);
}
}
}
}
4.2 邻接矩阵的广度优先遍历BFS
#include <queue>
void MGraph_BFS(MGraph* pGraph)
{
cout << "广度优先遍历:\n";
if (pGraph)
{
std::queue<int> queTmp;
bool bArrayVisited[NMAXVER] = { false };//避免重复访问
for (int i = 0;i<pGraph->nVCount;i++)
{
if (!bArrayVisited[i])
{
bArrayVisited[i] = true;
printf("%c ",pGraph->V[i]);
queTmp.push(i);
while (!queTmp.empty())
{
queTmp.pop();
for (int j = 0;j<pGraph->nVCount;j++)
{
if (false == bArrayVisited[j] && pGraph->E[i][j] == 1)
{
bArrayVisited[j] = true;
printf("%c ", pGraph->V[j]);
queTmp.push(j);
}
}
}
}
}
}
}
4.3 邻接矩阵测试
void main()
{
char v[] = { 'A','B','C','D','E','F'};//是一个指针数组
MGraph* graph = CreateGraph(v, 6);
AddEdge(graph, 0, 1);
AddEdge(graph, 0, 2);
AddEdge(graph, 0, 3);
AddEdge(graph, 1, 5);
AddEdge(graph, 1, 4);
AddEdge(graph, 2, 1);
AddEdge(graph, 3, 4);
//打印邻接矩阵
PrintLinJieArray(graph);
//深度优先遍历
MGraph_DFS(graph);
//广度优先遍历
MGraph_BFS(graph);
system("pause");
}
结果:
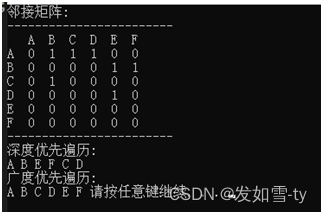
4.4 邻接表深度优先遍历DFS
void DFS(GraphList* pGraph,int v,bool visited[])
{
if (!pGraph)
{
return;
}
visited[v] = true;
printf("%c ", pGraph->V[v].data);
EdgeNode* pE = pGraph->V[v].firstEdge;
while (pE)
{
if (false == visited[pE->nvex])
{
DFS(pGraph, pE->nvex,visited);
}
pE = pE->next;
}
}
void Graph_DFS(GraphList* pGraph)
{
bool bVisited[NMAXVER] = { false };
for (int i = 0;i<pGraph->nVCount;i++)
{
if (false == bVisited[i])
{
DFS(pGraph, i, bVisited);
}
}
}
4.5 邻接表的广度优先遍历BFS
void Graph_BFS(GraphList* pGraph)
{
bool bVisited[NMAXVER] = { false };
std::queue<int> queTmp;
for (int i = 0;i<pGraph->nVCount;i++)
{
if (false == bVisited[i])
{
queTmp.push(i);
printf("%c ", pGraph->V[i].data);
bVisited[i] = true;
while (!queTmp.empty())
{
queTmp.pop();
EdgeNode* pE = pGraph->V[i].firstEdge;
while (pE)
{
if (false == bVisited[pE->nvex])
{
bVisited[pE->nvex] = true;
printf("%c ", pGraph->V[pE->nvex].data);
queTmp.push(pE->nvex);
}
pE = pE->next;
}
}
}
}
}
4.6 邻接表测试
//边表结点
struct EdgeNode
{
int nvex;//存储结点对应的下标
struct EdgeNode* next;//指向下一个邻接点
};
//顶点表结点
struct Vertex
{
char data;//数据
struct EdgeNode* firstEdge;//对应的下标
};
struct GraphList
{
Vertex V[NMAXVER];
int nVCount;//顶点个数
};
void printGraphList(GraphList* pGraph)
{
for (int i = 0;i<pGraph->nVCount;i++)
{
printf("%d %c ",i, pGraph->V[i].data);
EdgeNode* pChild = pGraph->V[i].firstEdge;
while (pChild)
{
cout << pChild->nvex << " ";
pChild = pChild->next;
}
cout << endl;
}
}
void main()
{
//A B C D E F
GraphList graph;
graph.nVCount = 6;
Vertex v0;
v0.data = 'A';
EdgeNode e3;
e3.nvex = 3;
e3.next = NULL;
EdgeNode e2;
e2.nvex = 2;
e2.next = &e3;
EdgeNode e1;
e1.nvex = 1;
e1.next = &e2;
v0.firstEdge = &e1;
graph.V[0] = v0;
Vertex v1;
v1.data = 'B';
EdgeNode e5;
e5.nvex = 5;
e5.next = NULL;
EdgeNode e4;
e4.nvex = 4;
e4.next = &e5;
v1.firstEdge = &e4;
graph.V[1] = v1;
Vertex v2;
v2.data = 'C';
EdgeNode eB;
eB.nvex = 1;
eB.next = NULL;
v2.firstEdge = &eB;
graph.V[2] = v2;
Vertex v3;
v3.data = 'D';
EdgeNode eE;
eE.nvex = 4;
eE.next = NULL;
v3.firstEdge = &eE;
graph.V[3] = v3;
Vertex v4;
v4.data = 'E';
v4.firstEdge = NULL;
graph.V[4] = v4;
Vertex v5;
v5.data = 'F';
v5.firstEdge = NULL;
graph.V[5] = v5;
printGraphList(&graph);
Graph_DFS(&graph);
cout << endl;
Graph_BFS(&graph);
system("pause");
}
结果:
























 6377
6377











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










