【NOIP2016提高A组模拟9.3】看电影

题目

Description

听说NOIP2016大家都考得不错，于是CCF奖励省常中了 K 张变形金刚5的电影票奖励OI队的同学去看电影。可是省常中OI队的同学们共有 N（N >= K）人。于是机智的你想到了一个公平公正的方法决定哪K人去看电影。
N个人排成一圈，按顺时针顺序标号为1 - N，每次随机一个还存活的人的编号，将这个人踢出。继续上述操作，直到剩下K个人。
但这样显然太无聊了，于是小S又想出一个牛逼的方法。
N个人排成一圈，按顺时针顺序标号为1 - N，每次随机一个1 - N的编号，假设随机到的编号是X，如果编号为X人还未踢出，则将这个人踢出，否则看编号为X % N + 1（即顺时针顺序下一个编号）的人是否存活，如果还未踢出则将他踢出，否则继续看编号（X + 1）% N +1的人，如果已被踢出看顺时针的下一个…………，以此类推，直到踢出一个人为止。重复上述操作，直到剩下K个人。
已知小S的编号是Id，问按照小S的方法来他有多少的概率可以不被踢出，成功得到看电影的机会。

Input

第一行包括三个正整数，N，K，Id（1<=K<=N<=10^9,1<=ID<=N ）

Output

一行一个最简分数，表示小S可以看到电影的概率。
（如果概率为1或0，请输出1/1或0/1）

Sample Input

2 1 2

Sample Output

1/2
【样例解释】
一共两个人，筛选经过1轮，第1轮每个人被踢出的概率都是等概率的，所以答案是1/2。

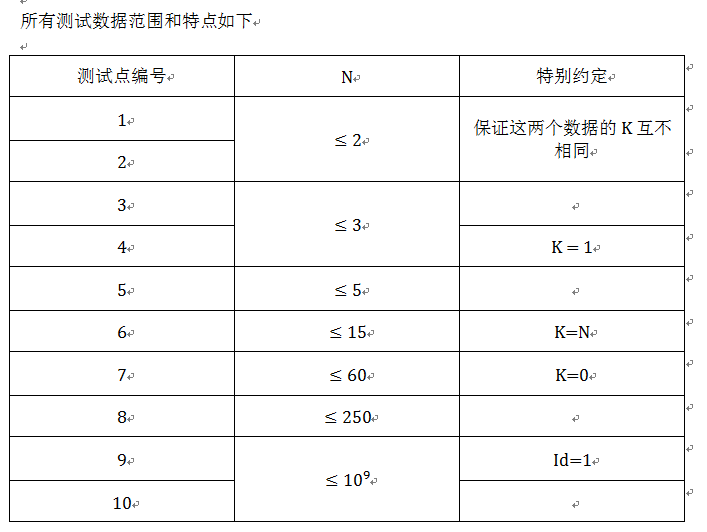
Data Constraint

比赛时の想法

一开始觉得这题好难啊，就去做后面的题目了，但是发现后面的题目都挺简单的，就开始重新以一道简单题的思路来审视这道题，发现这个选法对每个人都是公平的，那每个人的概率就是k/n嘛~（注意约分以及k=0的情况）

正解

在上面

var
    n,k,x,i,j:longint;
function gcd(x,y:longint):longint;
begin
    if y=0 then exit(x) else exit(gcd(y,x mod y));
end;
begin
    readln(n,k,x);
    if k=0 then
    begin
        writeln('0/1');
        halt;
    end;
    if n=k then
    begin
        writeln('1/1');
        halt;
    end;
    x:=gcd(n,k);
    writeln(k div x,'/',n div x);
end.