第一部分:矩阵的奇异值分解:
矩阵的奇异值分解证明过程中会用到五个定理,先作为补充知识展示这五个定理:
定理一:A是对称矩阵,则不同特征值对应的特征向量是正交的。
证明:设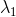 ,
,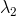 是矩阵A的特征向量,且
是矩阵A的特征向量,且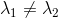 ,
,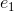 ,
,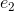 为
为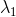 ,
,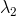 对应的特征向量,即:
对应的特征向量,即:
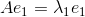 ,
,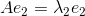
则
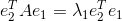 ,
,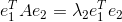
因为A是对称矩阵,则
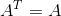
所以,
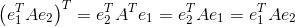
则:
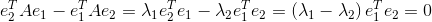
因为
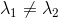 ,
,
所以:
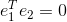 ,
,
即: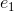 和
和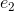 是正交的。证毕
是正交的。证毕
————————————————————————————————————————————————————————————————————————————
定理二:矩阵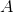 和它的转置
和它的转置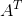 具有相同的特征值
具有相同的特征值
证明:因为:
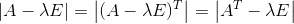 ,
,
即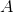 和
和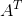 有相同的特征多项式,所以有相同的特征值。
有相同的特征多项式,所以有相同的特征值。
————————————————————————————————————————————————————————————————————————————
定理三:半正定矩阵的特征值均大于等于零
证明:这是半正定矩阵的定义
————————————————————————————————————————————————————————————————————————————
定理四:若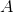 满足
满足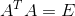 ,则称
,则称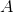 是单位正交矩阵
是单位正交矩阵
单位正交矩阵有如下的性质: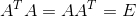 。
。
————————————————————————————————————————————————————————————————————————————
定理五:若矩阵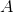 的秩为r,则
的秩为r,则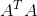 和
和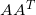 秩均为r。
秩均为r。
————————————————————————————————————————————————————————————————————————————
补充完以上五个定理,我们正式开始矩阵的奇异值分解的证明。
设矩阵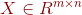 ,矩阵的秩为
,矩阵的秩为![]() ,且
,且 ,则矩阵可以分解为如下形式:
,则矩阵可以分解为如下形式:
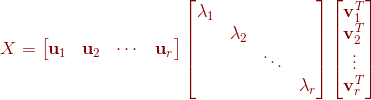 ,
,
也可表示为:
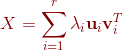
证明:无非就是寻找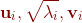 。
。
显然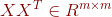 ,
,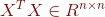 ,且这两个矩阵均是半正定矩阵,且互为转置,且根据定理五,这两个矩阵的秩均为
,且这两个矩阵均是半正定矩阵,且互为转置,且根据定理五,这两个矩阵的秩均为![]() 。根据定理二和定理三,这两个矩阵的特征值是相同的,且均大于等于零。我们只用大于零的特征值。设
。根据定理二和定理三,这两个矩阵的特征值是相同的,且均大于等于零。我们只用大于零的特征值。设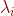 (我们按从大到小排序即:
(我们按从大到小排序即:![]() )是它们的不为零的特征值,且对于矩阵
)是它们的不为零的特征值,且对于矩阵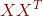 对应的单位特征向量为
对应的单位特征向量为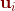 (
(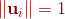 ),对于矩阵
),对于矩阵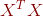 对应的单位特征向量为
对应的单位特征向量为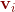 (
( ),即
),即
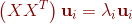 ,
,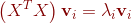 。
。
其实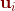 和
和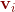 存在一定的关系,下面就找出这种关系。
存在一定的关系,下面就找出这种关系。
因为
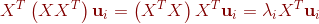 ,
,
所以,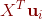 是
是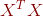 的特征向量,又因为
的特征向量,又因为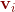 也是
也是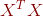 的特征向量,所以,
的特征向量,所以,
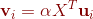 ,
,
又因为
 ,
,
所以:
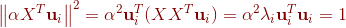 。
。
则:
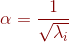 ,
,
所以,
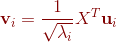 ,
,
那么
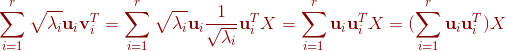
下面证明
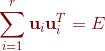 ,
,
其中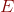 代表单位矩阵。
代表单位矩阵。
因为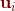 是对称矩阵
是对称矩阵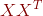 的不同特征值对应的特征向量,根据定理一,我们得出他们是相互正交的,又因为
的不同特征值对应的特征向量,根据定理一,我们得出他们是相互正交的,又因为
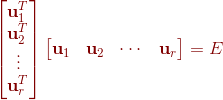 ,
,
然后,然后根据定理四,我们便得到
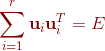
所以:
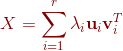 。
。
证毕。
矩阵的奇异值分解定理:
设矩阵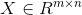 ,秩为
,秩为 ,
,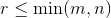 ,则该矩阵可以分解为:
,则该矩阵可以分解为:
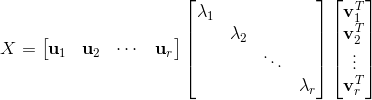
也可以表示为:
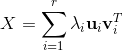 。
。
其中: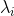 为矩阵
为矩阵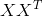 (或者
(或者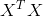 )的非零向量,
)的非零向量,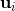 为
为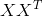 的对应特征向量,
的对应特征向量,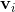 为
为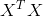 的对应特征向量,
的对应特征向量,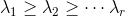 。
。
SVD的第一个作用之低秩近似(Low Rank Approximation):
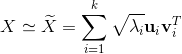 ,
,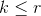 ,
,
即用矩阵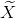 近似
近似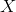 。
。
SVD的第二个作用之特征降维(Dimensionality Reduction):
假设特征是按列存储的,即:
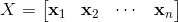 ,
,
其中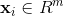 ,
,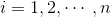 。
。
我们在低秩近似中已经用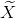 近似表示
近似表示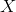 了。
了。
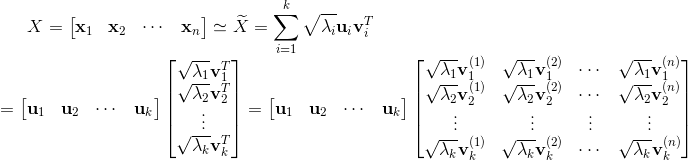
则根据分块矩阵的乘法,我们很容易得到:
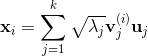 ,
,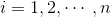 。
。
令:
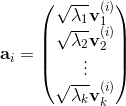 。
。
因为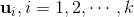 ,是相互正交的,所以根据
,是相互正交的,所以根据
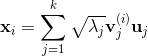 ,
,
显然可以得出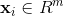 ,可以近似由
,可以近似由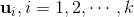 ,张成,所以我们得出结论:
,张成,所以我们得出结论:
m维的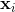 ,可以降到
,可以降到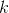 维的
维的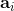 ,
,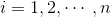 。
。























 1446
1446

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








