文章目录
引言
具有一个隐藏层的平面数据分类
欢迎来到您的第 3 周编程作业。 是时候构建你的第一个神经网络了,它会有一个隐藏层。 您将看到此模型与您使用逻辑回归实现的模型之间的巨大差异。
你将学到如何:
- 使用单个隐藏层实现 2 类分类神经网络
- 使用具有非线性激活函数的单位,例如 tanh
- 计算交叉熵损失
- 实现前向和后向传播
1 - 导入相关包
让我们首先导入您在此任务中需要的所有包。
- numpy 是使用 Python 进行科学计算的基本包。
- sklearn 为数据挖掘和数据分析提供了简单高效的工具
- matplotlib 是一个用于在 Python 中绘制图形的库
- testCases 提供了一些测试示例来评估您的函数的正确性
- planar_utils 提供了在这个任务中使用的各种有用的函数
# Package imports
import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
%matplotlib inline
np.random.seed(1) #设置固定的随机种子,使结果一致
2 - 数据集
首先,让我们获取您将要处理的数据集。 以下代码将“花”2 类数据集加载到变量 X 和 Y 中。
X, Y = load_planar_dataset()
使用 matplotlib 可视化数据集。 数据看起来像一朵“花”,带有一些红色(标签 y=0)和一些蓝色(y=1)点。 您的目标是构建一个模型来拟合这些数据。
# 数据可视化:
# plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);
plt.scatter(X[0, :], X[1, :], c= np.squeeze(Y), s=40, cmap=plt.cm.Spectral);
注意这里如果运行注释里的语句(也就是作业给出的语句),是会报错的
解决办法:需要把原来的c=Y改为np.squeeze(Y),并修改planar_utils.py 里的 plt.scatter() 函数,把 y 换成 np.squeeze(y),具体操作见链接
关于np.squeeze()函数的用法见链接
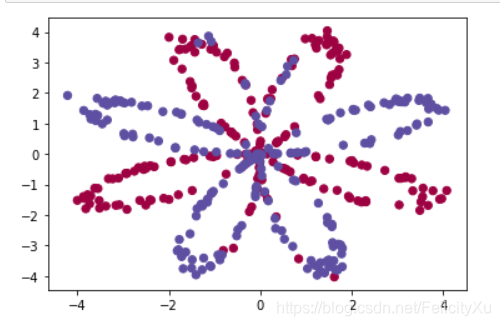
你有:
- 一个包含你的特征 (x1, x2) 的 numpy-array (matrix) X
- 一个包含标签的 numpy 数组(向量)Y(红色:0,蓝色:1)。
让我们首先更好地了解我们的数据是什么样的。
【练习】:你有多少训练样例? 另外,变量 X 和 Y 的形状是什么?
提示:如何获得 numpy 数组的形状?(help)
### START CODE HERE ### (≈ 3 lines of code)
shape_X = X.shape
shape_Y = Y.shape
m = shape_X[1] # training set size
### END CODE HERE ###
print ('The shape of X is: ' + str(shape_X)) # X的维度
print ('The shape of Y is: ' + str(shape_Y)) # Y的维度
print ('I have m = %d training examples!' % (m)) # 我有 个训练样本!
输出结果:
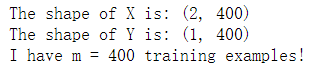
3 - 简单逻辑回归
在构建完整的神经网络之前,让我们先看看逻辑回归在这个问题上的表现。 您可以使用 sklearn 的内置函数来做到这一点。 运行下面的代码以在数据集上训练逻辑回归分类器。
#训练逻辑回归分类器
clf = sklearn.linear_model.LogisticRegressionCV();
clf.fit(X.T, Y.T);
运行后会打印如下信息:

您现在可以绘制这些模型的决策边界。 运行下面的代码。
# 绘制逻辑回归的决策边界
plot_decision_boundary(lambda x: clf.predict(x), X, Y)
plt.title("Logistic Regression")
# 打印逻辑回归的准确度
LR_predictions = clf.predict(X.T)
print ('Accuracy of logistic regression: %d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +
'% ' + "(percentage of correctly labelled datapoints)")
关于python中lambda表达式的介绍:链接
输出结果:
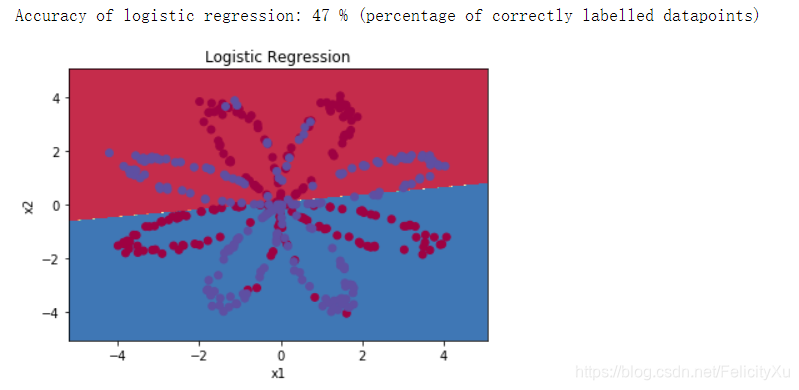
解释:数据集不是线性可分的,因此逻辑回归表现不佳。 希望神经网络会做得更好。 让我们现在试试这个!
4 - 神经网络模型
逻辑回归在“花数据集”上效果不佳。 您将训练一个具有单个隐藏层的神经网络。
这是我们的模型:
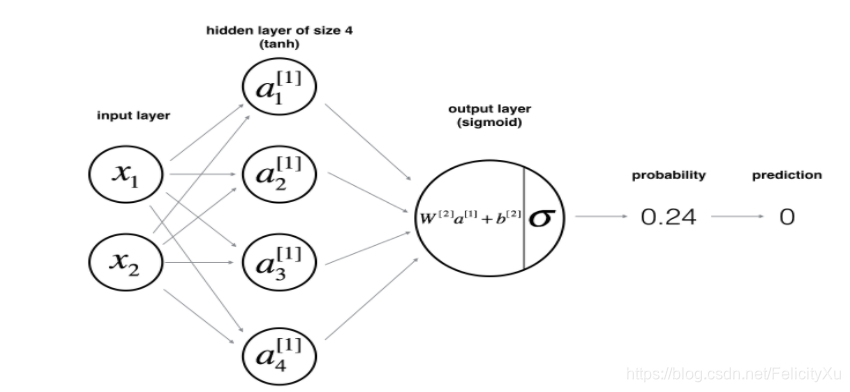
数学上:
对于一个样本
x
(
i
)
x^{(i)}
x(i):
z
[
1
]
(
i
)
=
W
[
1
]
x
(
i
)
+
b
[
1
]
(
i
)
(1)
z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)}\tag{1}
z[1](i)=W[1]x(i)+b[1](i)(1)
a
[
1
]
(
i
)
=
tanh
(
z
[
1
]
(
i
)
)
(2)
a^{[1] (i)} = \tanh(z^{[1] (i)})\tag{2}
a[1](i)=tanh(z[1](i))(2)
z
[
2
]
(
i
)
=
W
[
2
]
a
[
1
]
(
i
)
+
b
[
2
]
(
i
)
(3)
z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2] (i)}\tag{3}
z[2](i)=W[2]a[1](i)+b[2](i)(3)
y
^
(
i
)
=
a
[
2
]
(
i
)
=
σ
(
z
[
2
]
(
i
)
)
(4)
\hat{y}^{(i)} = a^{[2] (i)} = \sigma(z^{ [2] (i)})\tag{4}
y^(i)=a[2](i)=σ(z[2](i))(4)
 (5)
(5)
鉴于对所有示例的预测,您还可以按如下方式计算成本
J
J
J:
J
=
−
1
m
∑
i
=
0
m
(
y
(
i
)
log
(
a
[
2
]
(
i
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
a
[
2
]
(
i
)
)
)
(6)
J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large\left(\small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large \right) \small \tag{6}
J=−m1i=0∑m(y(i)log(a[2](i))+(1−y(i))log(1−a[2](i)))(6)
提醒:构建神经网络的一般方法是:
- 定义神经网络结构(输入单元数量、隐藏单元数量等)。
- 初始化模型参数
- 循环:
- 实现前向传播
- 计算损失
- 实现反向传播以获得梯度
- 更新参数(梯度下降)
您经常构建辅助函数来计算步骤 1-3,然后将它们合并为一个我们称为nn_model()的函数。 一旦您构建了nn_model()并学习了正确的参数,您就可以对新数据进行预测。
4.1 - 定义神经网络结构
【练习】:定义三个变量:
- n_x:输入层的大小
- n_h:隐藏层的大小(设置为4)
- n_y:输出层的大小
提示:使用 X 和 Y 的形状来找到 n_x 和 n_y。 此外,将隐藏层大小硬编码为 4。
# GRADED FUNCTION: layer_sizes
def layer_sizes(X, Y):
"""
Arguments(参数):
X -- 输入数据集(输入大小,示例数量)
Y -- 标签(输出大小,示例数量)
Returns(返回):
n_x -- 输入层大小
n_h -- 隐藏层大小
n_y -- 输出层大小
"""
### START CODE HERE ### (≈ 3 lines of code)
n_x = X.shape[0] # size of input layer
n_h = 4
n_y = Y.shape[0] # size of output layer
### END CODE HERE ###
return (n_x, n_h, n_y)
X_assess, Y_assess = layer_sizes_test_case()
(n_x, n_h, n_y) = layer_sizes(X_assess, Y_assess)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))
输出结果为:

4.2 - 初始化模型参数
【练习】:实现函数initialize_parameters()。
【指示】:
- 确保您的参数大小正确。 如果需要,请参考上面的神经网络图。
- 您将使用随机值初始化权重矩阵。
- 使用:
np.random.randn(a,b) * 0.01随机初始化形状为 (a,b) 的矩阵。
- 使用:
- 您将偏置向量初始化为零。
- 使用:
np.zeros((a,b))用零初始化形状为 (a,b) 的矩阵。
- 使用:
# GRADED FUNCTION: initialize_parameters
def initialize_parameters(n_x, n_h, n_y):
"""
Argument(参数):
n_x -- 输入层大小
n_h -- 隐藏层大小
n_y -- 输出层大小
Returns(返回):
params -- 包含参数的python字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
"""
np.random.seed(2) # 我们设置了一个种子,以便您的输出与我们的输出匹配,尽管初始化是随机的。
### START CODE HERE ### (≈ 4 lines of code)
W1 = np.random.randn(n_h, n_x) * 0.01
b1 = np.zeros((n_h, 1))
W2 = np.random.randn(n_y, n_h) * 0.01
b2 = np.zeros((n_y, 1))
### END CODE HERE ###
assert (W1.shape == (n_h, n_x))
assert (b1.shape == (n_h, 1))
assert (W2.shape == (n_y, n_h))
assert (b2.shape == (n_y, 1))
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
n_x, n_h, n_y = initialize_parameters_test_case()
parameters = initialize_parameters(n_x, n_h, n_y)
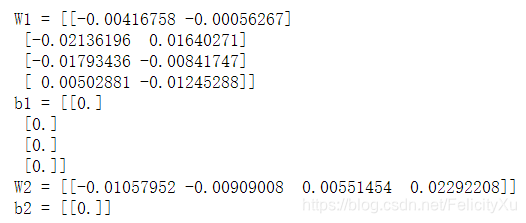
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
输出结果为:
4.3 - 循环
【问题】:实现forward_propagation()。
【指示】:
- 看看上面你的分类器的数学表示。
- 您可以使用函数
sigmoid()。 它内置(导入)在笔记本中。 - 您也可以使用函数
np.tanh()。 它是numpy库的一部分。 - 您必须实施的步骤是:
- 使用
parameters[".."]从字典 "parameters"中(这是initialize_parameters()
的输出)检索每个参数。 - 实施前向传播。 计算 Z [ 1 ] , A [ 1 ] , Z [ 2 ] Z^{[1]}, A^{[1]}, Z^{[2]} Z[1],A[1],Z[2] 和 A [ 2 ] A^{[2]} A[2](您对训练集中所有示例的所有预测的向量)。
- 使用
- 反向传播所需的值存储在“缓存”中。 缓存将作为反向传播函数的输入。
# GRADED FUNCTION: forward_propagation
def forward_propagation(X, parameters):
"""
参数:
X - 维度为(n_x,m)的输入数据。
parameters - 初始化函数(initialize_parameters)的输出
返回:
A2 - 使用sigmoid()函数计算的第二次激活后的数值
cache - 包含“Z1”,“A1”,“Z2”和“A2”的字典类型变量
"""
# 从字典“参数”中检索每个参数
### START CODE HERE ### (≈ 4 lines of code)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
### END CODE HERE ###
# 实施前向传播来计算 A2(概率)
### START CODE HERE ### (≈ 4 lines of code)
Z1 = np.dot(W1, X) + b1
A1 = np.tanh(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = sigmoid(Z2)
### END CODE HERE ###
assert(A2.shape == (1, X.shape[1]))
cache = {"Z1": Z1,
"A1": A1,
"Z2": Z2,
"A2": A2}
return A2, cache
X_assess, parameters = forward_propagation_test_case()
A2, cache = forward_propagation(X_assess, parameters)
# Note:我们在这里使用平均值只是为了确保您的输出与我们的匹配。
print(np.mean(cache['Z1']) ,np.mean(cache['A1']),np.mean(cache['Z2']),np.mean(cache['A2']))
输出结果为:
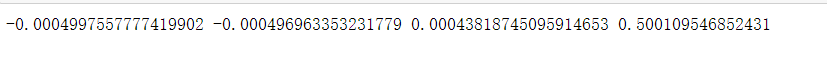
现在您已经计算了
A
[
2
]
A^{[2]}
A[2](在 Python 变量“A2”中),其中包含每个示例的
a
[
2
]
(
i
)
a^{[2](i)}
a[2](i),您可以计算成本函数为如下:
J
=
−
1
m
∑
i
=
0
m
(
y
(
i
)
log
(
a
[
2
]
(
i
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
a
[
2
]
(
i
)
)
)
(13)
J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large{(} \small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large{)} \small\tag{13}
J=−m1i=0∑m(y(i)log(a[2](i))+(1−y(i))log(1−a[2](i)))(13)
【练习】:实现compute_cost()来计算成本 𝐽的值。
【指示】:
有很多方法可以实现交叉熵损失。 为了帮助您,我们为您提供了我们将如何实施
−
∑
i
=
0
m
y
(
i
)
log
(
a
[
2
]
(
i
)
)
- \sum\limits_{i=0}^{m} y^{(i)}\log(a^{[2](i)})
−i=0∑my(i)log(a[2](i)):
logprobs = np.multiply(np.log(A2),Y)
cost = - np.sum(logprobs) # 不需要for循环!
(您可以使用 np.multiply() 然后使用 np.sum() 或直接使用 np.dot())。
python中np.multiply()、np.dot()和星号(*)三种乘法运算的区别
# GRADED FUNCTION: compute_cost
def compute_cost(A2, Y, parameters):
"""
计算等式 (13) 中给出的交叉熵成本
Arguments:
A2 -- 第二次激活的 sigmoid 输出,维度为 (1, number of examples)
Y -- “真实true”标签向量,维度为(1,示例数量)
parameters -- 包含参数 W1、b1、W2 和 b2 的 python 字典
Returns:
cost -- 给定方程(13)的交叉熵成本
"""
m = Y.shape[1] # 样本数量
# 计算交叉熵成本
### START CODE HERE ### (≈ 2 lines of code)
logprobs = np.multiply(np.log(A2), Y) + np.multiply(np.log(1 - A2), 1-Y)
# 也可以直接logprobs = Y*np.log(A2) + (1-Y)* np.log(1-A2)
cost =-1 / m * np.sum(logprobs)
### END CODE HERE ###
cost = np.squeeze(cost) # 确保成本是我们所期望的
# E.g., turns [[17]] into 17
assert(isinstance(cost, float))
return cost
A2, Y_assess, parameters = compute_cost_test_case()
print("cost = " + str(compute_cost(A2, Y_assess, parameters)))
输出结果为:
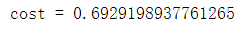
使用在前向传播期间计算的缓存,您现在可以实现后向传播。
【练习(问题)】:实现函数backward_propagation()。
说明:反向传播通常是深度学习中最难(最数学)的部分。 为了帮助你,这里再次是反向传播讲座的幻灯片。 您需要使用这张幻灯片右侧的六个方程,因为您正在构建一个矢量化实现。

提示:
要计算 dZ1,您需要计算
g
[
1
]
′
(
Z
[
1
]
)
g^{[1]'}(Z^{[1]})
g[1]′(Z[1])。 由于
g
[
1
]
(
.
)
g^{[1]}(.)
g[1](.)是tanh激活函数,如果
a
=
g
[
1
]
(
z
)
a = g^{[1]}(z)
a=g[1](z),那么
g
[
1
]
′
(
z
)
=
1
−
a
2
g^{[1]'}(z) = 1-a^2
g[1]′(z)=1−a2。 因此,您可以使用 (1 - np.power(A1, 2))
计
算
g
[
1
]
′
(
Z
[
1
]
)
计算g^{[1]'}(Z^{[1]})
计算g[1]′(Z[1]) 。
# GRADED FUNCTION: backward_propagation
def backward_propagation(parameters, cache, X, Y):
"""
使用上面的说明实现反向传播.
Arguments:
parameters -- 包含参数的python字典
cache -- 包含了 "Z1", "A1", "Z2" 和 "A2"参数的字典.
X -- 维度为(2, number of examples)的输入数据
Y -- "true" 标签向量,维度为(1, number of examples)
Returns:
grads -- 包含关于不同参数的梯度的python字典
"""
m = X.shape[1]
# 首先,从字典“参数”中检索W1和W2.
### START CODE HERE ### (≈ 2 lines of code)
W1 = parameters["W1"]
W2 = parameters["W2"]
### END CODE HERE ###
# 从字典“缓存”中检索 A1 和 A2.
### START CODE HERE ### (≈ 2 lines of code)
A1 = cache["A1"]
A2 = cache["A2"]
### END CODE HERE ###
# 反向传播: 计算 dW1, db1, dW2, db2.
### START CODE HERE ### (≈ 6 lines of code, corresponding to 6 equations on slide above)
dZ2 = A2 - Y
dW2 = 1 / m * np.dot(dZ2, A1.T)
db2 = 1 / m * np.sum(dZ2, axis = 1, keepdims = True)
dZ1 = np.dot(W2.T, dZ2) * (1 - np.power(A1, 2))
dW1 = 1 / m * np.dot(dZ1, X.T)
db1 = 1 / m * np.sum(dZ1, axis = 1, keepdims = True)
### END CODE HERE ###
grads = {"dW1": dW1,
"db1": db1,
"dW2": dW2,
"db2": db2}
return grads
parameters, cache, X_assess, Y_assess = backward_propagation_test_case()
grads = backward_propagation(parameters, cache, X_assess, Y_assess)
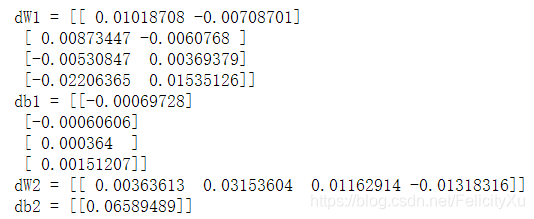
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))
输出结果为
【练习(问题)】:实现更新规则。 使用梯度下降。 您必须使用 (dW1, db1, dW2, db2) 才能更新 (W1, b1, W2, b2)。
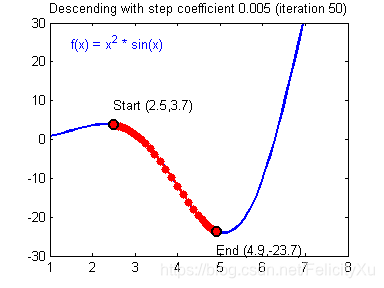
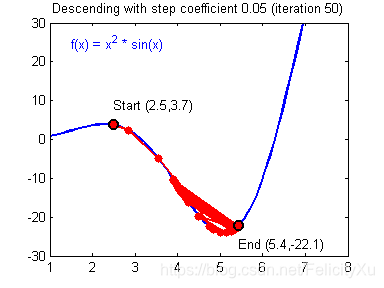
【一般梯度下降规则】: θ = θ − α ∂ J ∂ θ \theta = \theta - \alpha \frac{\partial J }{ \partial \theta } θ=θ−α∂θ∂J,其中α 是学习率,θ 表示参数。
插图:具有良好学习率(收敛)和糟糕学习率(发散)的梯度下降算法。 图片由亚当·哈利提供。(不知道这个图能不能动起来)
# GRADED FUNCTION: update_parameters
def update_parameters(parameters, grads, learning_rate = 1.2):
"""
使用上面给出的梯度下降更新规则更新参数
Arguments:
parameters -- 包含参数的python字典
grads -- 包含梯度的python字典
Returns:
parameters -- 包含更新参数的 python 字典
"""
# 从字典“参数”中检索每个参数
### START CODE HERE ### (≈ 4 lines of code)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
### END CODE HERE ###
# 从字典“grads”中检索每个梯度
### START CODE HERE ### (≈ 4 lines of code)
dW1 = grads["dW1"]
db1 = grads["db1"]
dW2 = grads["dW2"]
db2 = grads["db2"]
## END CODE HERE ###
# 每个参数的更新规则
### START CODE HERE ### (≈ 4 lines of code)
W1 = W1 - learning_rate * dW1
b1 = b1 - learning_rate * db1
W2 = W2 - learning_rate * dW2
b2 = b2 - learning_rate * db2
### END CODE HERE ###
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2}
return parameters
parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
输出结果为

4.4 - 在 nn_model() 中集成第 4.1、4.2 和 4.3 部分
【练习(问题)】:在nn_model()中构建您的神经网络模型。
【说明】:神经网络模型必须以正确的顺序使用前面的函数。
# GRADED FUNCTION: nn_model
def nn_model(X, Y, n_h, num_iterations = 10000, print_cost=False):
"""
参数:
X - 数据集,维度为(2,示例数)
Y - 标签,维度为(1,示例数)
n_h - 隐藏层的数量
num_iterations - 梯度下降循环中的迭代次数
print_cost - 如果为True,则每1000次迭代打印一次成本数值
返回:
parameters - 模型学习的参数,它们可以用来进行预测。
"""
np.random.seed(3)
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
# 初始化参数,然后检索 W1、b1、W2、b2。 输入:“n_x、n_h、n_y”。 输出 = "W1, b1, W2, b2, 参数"。
### START CODE HERE ### (≈ 5 lines of code)
parameters = initialize_parameters(n_x, n_h, n_y) # 初始化参数
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
### END CODE HERE ###
# 循环(梯度下降)
for i in range(0, num_iterations):
### START CODE HERE ### (≈ 4 lines of code)
# 前向传播。 输入:“X,parameters”。 输出:“A2,cache”。
A2, cache = forward_propagation(X, parameters)
# 成本函数. 输入 "A2, Y, parameters". 输出: "cost".
cost = compute_cost(A2, Y, parameters)
# 反向传播,输入: "parameters, cache, X, Y". 输出: "grads".
grads = backward_propagation(parameters, cache, X, Y)
# 梯度下降参数更新. 输入: "parameters, grads". 输出: "parameters".
parameters = update_parameters(parameters, grads)
### END CODE HERE ###
# Print the cost every 1000 iterations
if print_cost and i % 1000 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
return parameters
X_assess, Y_assess = nn_model_test_case()
parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))
输出结果为

4.5 预测
【问题】:通过构建predict()来使用您的模型进行预测。 使用前向传播来预测结果。
【提醒】:predictions =
y
p
r
e
d
i
c
t
i
o
n
=
1
activation > 0.5
=
{
1
if
a
c
t
i
v
a
t
i
o
n
>
0.5
0
otherwise
y_{prediction} = \mathbb 1 \text{{activation > 0.5}} = \begin{cases} 1 & \text{if}\ activation > 0.5 \\ 0 & \text{otherwise} \end{cases}
yprediction=1activation > 0.5={10if activation>0.5otherwise
例如,如果您想根据阈值将矩阵 X 的条目设置为 0 和 1,您可以这样做: X_new = (X > threshold)
# GRADED FUNCTION: predict
def predict(parameters, X):
"""
使用学习到的参数,为 X 中的每个示例预测一个类
Arguments:
parameters -- 包含参数的python字典
X -- 输入数据,维度为(n_x, m)
Returns
predictions -- 我们模型的预测向量 (red: 0 / blue: 1)
"""
# 使用前向传播计算概率,并使用 0.5 作为阈值分类为 0/1.
### START CODE HERE ### (≈ 2 lines of code)
A2, cache = forward_propagation(X, parameters)
predictions = np.round(A2) # 四舍五入
### END CODE HERE ###
return predictions
parameters, X_assess = predict_test_case()
predictions = predict(parameters, X_assess)
print("predictions mean = " + str(np.mean(predictions)))
输出结果为:
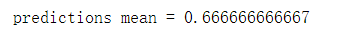
运行模型
是时候运行模型并查看它在平面数据集上的表现了。 运行以下代码以使用单个隐藏层 和𝑛ℎ 隐藏单元来测试您的模型。
# Build a model with a n_h-dimensional hidden layer
parameters = nn_model(X, Y, n_h = 4, num_iterations = 10000, print_cost=True)
# Plot the decision boundary
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
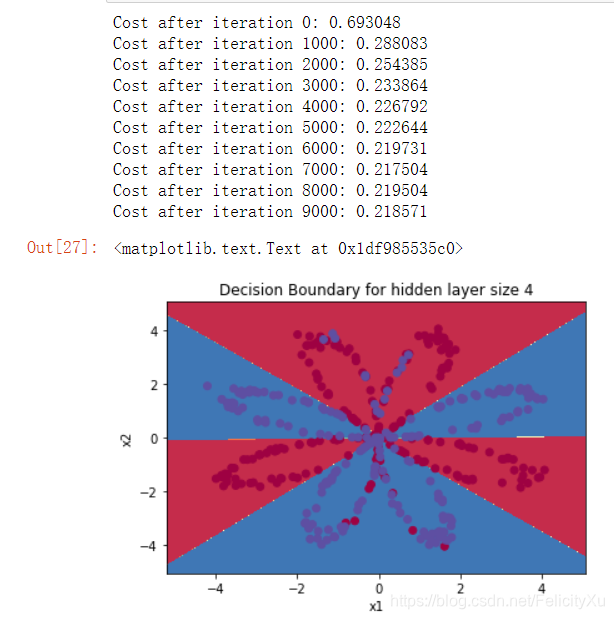
输出结果为
# 打印精度
predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100) + '%')
与 Logistic 回归相比,准确性确实很高。 模型已经学会了花的叶子图案! 与逻辑回归不同,神经网络甚至能够学习高度非线性的决策边界。
现在,让我们尝试几种隐藏层大小。
4.6 - 调整隐藏层大小(可选/未分级练习)
运行以下代码。 可能需要 1-2 分钟。 您将观察到模型对于各种隐藏层大小的不同行为。
# This may take about 2 minutes to run
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 10, 20]
for i, n_h in enumerate(hidden_layer_sizes):
plt.subplot(5, 2, i+1)
plt.title('Hidden Layer of size %d' % n_h)
parameters = nn_model(X, Y, n_h, num_iterations = 5000)
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
predictions = predict(parameters, X)
accuracy = float((np.dot(Y,predictions.T) + np.dot(1-Y,1-predictions.T))/float(Y.size)*100)
print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))

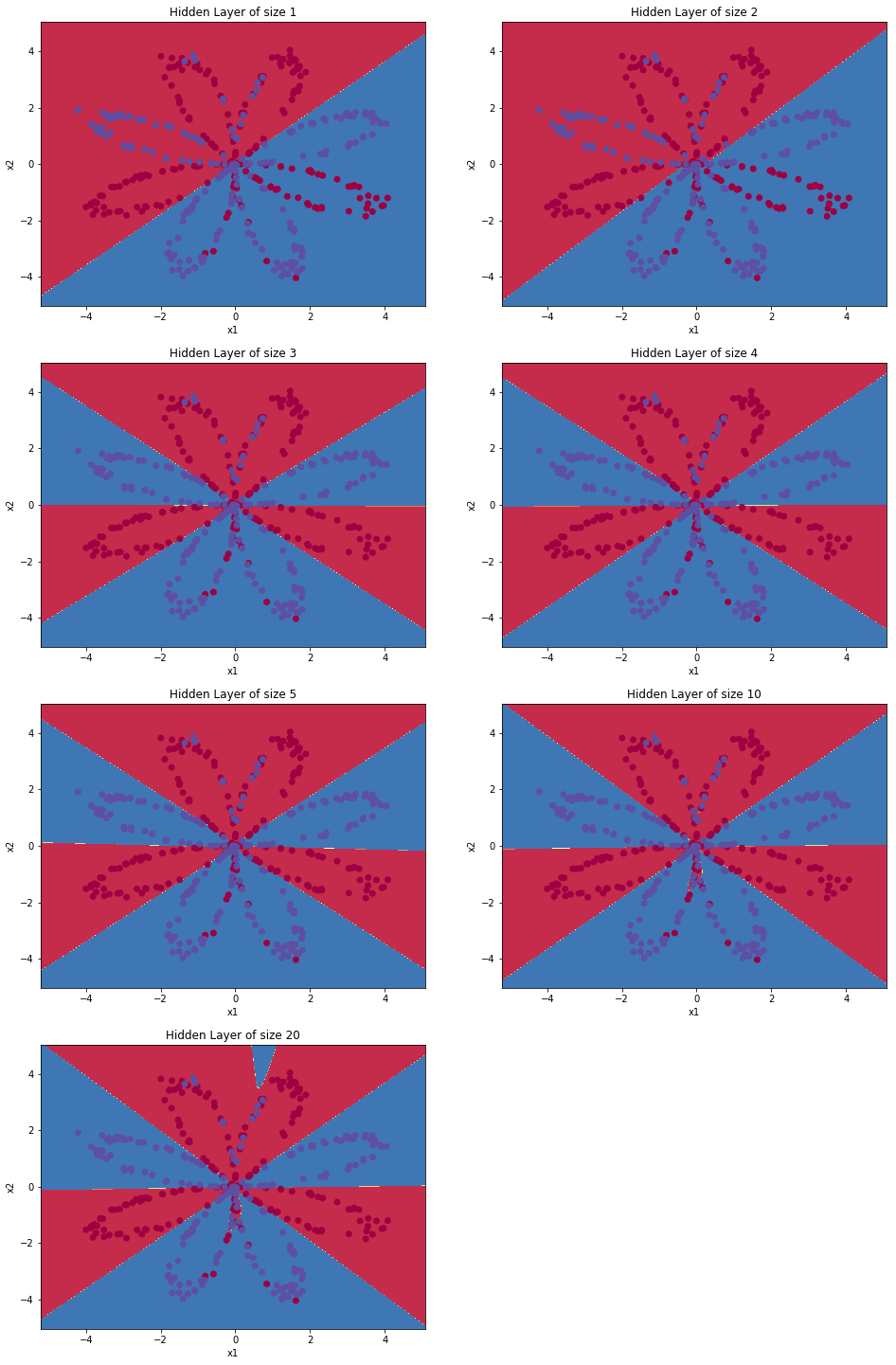
【解释】:
- 较大的模型(具有更多隐藏单元)能够更好地拟合训练集,直到最终最大的模型过度拟合数据。
- 最好的隐藏层大小似乎在 n_h = 5 左右。实际上,这里的值似乎很好地拟合了数据,而不会引起明显的过度拟合。
- 稍后您还将了解正则化,它使您可以使用非常大的模型(例如 n_h = 50)而不会过度拟合。
您已经学会了: - 构建一个带有隐藏层的完整神经网络 - 充分利用非线性单元 - 实施前向传播和反向传播,并训练神经网络 - 查看变化的影响 隐藏层大小,包括过拟合
5 - 在其它数据集上的表现
# Datasets
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()
datasets = {"noisy_circles": noisy_circles,
"noisy_moons": noisy_moons,
"blobs": blobs,
"gaussian_quantiles": gaussian_quantiles}
### START CODE HERE ### (choose your dataset)
dataset = "gaussian_quantiles"
### END CODE HERE ###
X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])
# make blobs binary
if dataset == "blobs":
Y = Y%2
# Visualize the data
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);
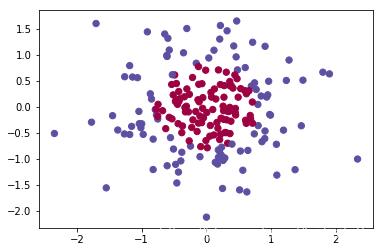
附录:planar_utils.py
import matplotlib.pyplot as plt
import numpy as np
import sklearn
import sklearn.datasets
import sklearn.linear_model
def plot_decision_boundary(model, X, y):
# Set min and max values and give it some padding
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = model(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
plt.ylabel('x2')
plt.xlabel('x1')
plt.scatter(X[0, :], X[1, :], c= np.squeeze(y), cmap=plt.cm.Spectral)
def sigmoid(x):
"""
Compute the sigmoid of x
Arguments:
x -- A scalar or numpy array of any size.
Return:
s -- sigmoid(x)
"""
s = 1/(1+np.exp(-x))
return s
def load_planar_dataset():
np.random.seed(1)
m = 400 # number of examples
N = int(m/2) # number of points per class
D = 2 # dimensionality
X = np.zeros((m,D)) # data matrix where each row is a single example
Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue)
a = 4 # maximum ray of the flower
for j in range(2):
ix = range(N*j,N*(j+1))
t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
Y[ix] = j
X = X.T
Y = Y.T
return X, Y
def load_extra_datasets():
N = 200
noisy_circles = sklearn.datasets.make_circles(n_samples=N, factor=.5, noise=.3)
noisy_moons = sklearn.datasets.make_moons(n_samples=N, noise=.2)
blobs = sklearn.datasets.make_blobs(n_samples=N, random_state=5, n_features=2, centers=6)
gaussian_quantiles = sklearn.datasets.make_gaussian_quantiles(mean=None, cov=0.5, n_samples=N, n_features=2, n_classes=2, shuffle=True, random_state=None)
no_structure = np.random.rand(N, 2), np.random.rand(N, 2)
return noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure
附录:testCases.py
import numpy as np
def layer_sizes_test_case():
np.random.seed(1)
X_assess = np.random.randn(5, 3)
Y_assess = np.random.randn(2, 3)
return X_assess, Y_assess
def initialize_parameters_test_case():
n_x, n_h, n_y = 2, 4, 1
return n_x, n_h, n_y
def forward_propagation_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
parameters = {'W1': np.array([[-0.00416758, -0.00056267],
[-0.02136196, 0.01640271],
[-0.01793436, -0.00841747],
[ 0.00502881, -0.01245288]]),
'W2': np.array([[-0.01057952, -0.00909008, 0.00551454, 0.02292208]]),
'b1': np.array([[ 0.],
[ 0.],
[ 0.],
[ 0.]]),
'b2': np.array([[ 0.]])}
return X_assess, parameters
def compute_cost_test_case():
np.random.seed(1)
Y_assess = np.random.randn(1, 3)
parameters = {'W1': np.array([[-0.00416758, -0.00056267],
[-0.02136196, 0.01640271],
[-0.01793436, -0.00841747],
[ 0.00502881, -0.01245288]]),
'W2': np.array([[-0.01057952, -0.00909008, 0.00551454, 0.02292208]]),
'b1': np.array([[ 0.],
[ 0.],
[ 0.],
[ 0.]]),
'b2': np.array([[ 0.]])}
a2 = (np.array([[ 0.5002307 , 0.49985831, 0.50023963]]))
return a2, Y_assess, parameters
def backward_propagation_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
Y_assess = np.random.randn(1, 3)
parameters = {'W1': np.array([[-0.00416758, -0.00056267],
[-0.02136196, 0.01640271],
[-0.01793436, -0.00841747],
[ 0.00502881, -0.01245288]]),
'W2': np.array([[-0.01057952, -0.00909008, 0.00551454, 0.02292208]]),
'b1': np.array([[ 0.],
[ 0.],
[ 0.],
[ 0.]]),
'b2': np.array([[ 0.]])}
cache = {'A1': np.array([[-0.00616578, 0.0020626 , 0.00349619],
[-0.05225116, 0.02725659, -0.02646251],
[-0.02009721, 0.0036869 , 0.02883756],
[ 0.02152675, -0.01385234, 0.02599885]]),
'A2': np.array([[ 0.5002307 , 0.49985831, 0.50023963]]),
'Z1': np.array([[-0.00616586, 0.0020626 , 0.0034962 ],
[-0.05229879, 0.02726335, -0.02646869],
[-0.02009991, 0.00368692, 0.02884556],
[ 0.02153007, -0.01385322, 0.02600471]]),
'Z2': np.array([[ 0.00092281, -0.00056678, 0.00095853]])}
return parameters, cache, X_assess, Y_assess
def update_parameters_test_case():
parameters = {'W1': np.array([[-0.00615039, 0.0169021 ],
[-0.02311792, 0.03137121],
[-0.0169217 , -0.01752545],
[ 0.00935436, -0.05018221]]),
'W2': np.array([[-0.0104319 , -0.04019007, 0.01607211, 0.04440255]]),
'b1': np.array([[ -8.97523455e-07],
[ 8.15562092e-06],
[ 6.04810633e-07],
[ -2.54560700e-06]]),
'b2': np.array([[ 9.14954378e-05]])}
grads = {'dW1': np.array([[ 0.00023322, -0.00205423],
[ 0.00082222, -0.00700776],
[-0.00031831, 0.0028636 ],
[-0.00092857, 0.00809933]]),
'dW2': np.array([[ -1.75740039e-05, 3.70231337e-03, -1.25683095e-03,
-2.55715317e-03]]),
'db1': np.array([[ 1.05570087e-07],
[ -3.81814487e-06],
[ -1.90155145e-07],
[ 5.46467802e-07]]),
'db2': np.array([[ -1.08923140e-05]])}
return parameters, grads
def nn_model_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
Y_assess = np.random.randn(1, 3)
return X_assess, Y_assess
def predict_test_case():
np.random.seed(1)
X_assess = np.random.randn(2, 3)
parameters = {'W1': np.array([[-0.00615039, 0.0169021 ],
[-0.02311792, 0.03137121],
[-0.0169217 , -0.01752545],
[ 0.00935436, -0.05018221]]),
'W2': np.array([[-0.0104319 , -0.04019007, 0.01607211, 0.04440255]]),
'b1': np.array([[ -8.97523455e-07],
[ 8.15562092e-06],
[ 6.04810633e-07],
[ -2.54560700e-06]]),
'b2': np.array([[ 9.14954378e-05]])}
return parameters, X_assess
























 1295
1295











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








