【brainpy学习笔记】简化神经元模型2——ExpIF、AdEx、Izhikevich模型

Fellyhosn

已于 2023-06-24 14:47:17 修改

阅读量1.6k

点赞数 2

分类专栏：计算神经科学文章标签：学习笔记 python 神经网络

于 2023-04-19 20:45:00 首次发布

本文链接：https://blog.csdn.net/Fellyhosn/article/details/130222363

版权

计算神经科学专栏收录该内容

11 篇文章

订阅专栏

文章介绍了神经计算中的几种简化模型，包括ExpIF模型、AdEx模型和Izhikevich模型。ExpIF模型通过指数积分改进了LIF模型，AdEx模型进一步引入适应性变量模拟神经元的适应行为，而Izhikevich模型结合了二阶动力学，能展现更多样化的神经元发放模式。每个模型的代码实现和参数影响都在文中详细说明。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

参考书目：《神经计算建模实战——基于brainpy》吴思

书接上文：【brainpy学习笔记】简化神经元模型1——LIF、QIF模型https://blog.csdn.net/Fellyhosn/article/details/130208409?spm=1001.2014.3001.5501

3 指数整合发放（ExpIF）模型

3.1 ExpIF模型定义与代码实现

ExpIF模型在原始的LIF模型上进行了修改，通过指数积分的形式提升模型生成动作电位的真实度，其数学模型表达式如下：

$\left\{\begin{matrix} \tau\frac{dV}{dt}=-(V-V_{rest})+\Delta_Te^{\frac{V-V_T}{\Delta_T}} +RI(t) \\ \text{if}\quad V>\theta,\quad V\leftarrow V_{reset}\quad \text{last}\quad t_{ref} \end{matrix}\right.$

第一个方程右侧的第一项为膜电位衰减项（同LIF），第二项为指数项， $\Delta_T$ 表示电位增长的陡峭程度， $V_T$ 表示神经元的兴奋阈值。因为指数项增长快，因此 $\theta$ 的取值几乎不会影响膜电位到达 $\theta$ 的时间。但是指数项的引入使得ExpIF模型无法像QIF模型一样求得解析解。

用brainpy实现ExpIF模型如下：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class ExpIF(bp.dyn.NeuGroup):
    def __init__(self,size,V_rest=-65.,V_reset=-68.,V_th=20.,V_T=-59.9,delta_T=3.48,R=1.,tau=10.,t_ref=2.,name=None):
        super(ExpIF,self).__init__(size=size,name=name)

        #初始化参数
        self.V_rest = V_rest
        self.V_reset = V_reset
        self.V_th = V_th
        self.V_T =V_T
        self.delta_T =delta_T
        self.R = R
        self.tau = tau
        self.t_ref = t_ref

        #初始化变量
        self.V = bm.Variable(bm.random.randn(self.num) + V_reset)
        self.input = bm.Variable(bm.zeros(self.num))
        self.t_last_spike = bm.Variable(bm.ones(self.num)* -1e7) #上一次脉冲发放时刻
        self.refractory = bm.Variable(bm.zeros(self.num,dtype=bool)) #是否处于不应期
        self.spike = bm.Variable(bm.zeros(self.num,dtype=bool)) #脉冲发放状态

        #积分函数:使用指数欧拉方法积分
        self.integral = bp.odeint(f=self.derivative,method='exponential_euler')

        #定义膜电位关于时间变化的微分方程
    def derivative(self,V,t,Iext):
        exp_v = self.delta_T * bm.exp((V-self.V_T)/self.delta_T)
        dvdt = (- (V - self.V_rest) + exp_v +self.R * Iext)/self.tau
        return dvdt

        #更新函数
    def update(self,tdi):
        t,dt = tdi.t,tdi.dt
        refractory = (t - self.t_last_spike) <= self.t_ref #是否处于不应期
        V = self.integral(self.V,t,self.input,dt=dt) #根据时间步长更新膜电位
        V = bm.where(refractory,self.V,V)
        spike = V>self.V_th #更新脉冲状态
        self.spike.value = spike
        self.t_last_spike = bm.where(spike,t,self.t_last_spike) #更新上次脉冲时间
        self.V.value = bm.where(spike,self.V_reset,V)
        self.refractory.value = bm.logical_or(refractory,spike)
        self.input[:]=0#重置外界输入

group = ExpIF(1)
runner = bp.dyn.DSRunner(group,monitors=['V'],inputs=('input',5.),dt=0.01)
runner(500)
plt.plot(runner.mon.ts,runner.mon.V)
plt.xlabel('t(ms)')
plt.ylabel('V')
plt.show()

在恒定电流输入下，ExpIF模型的膜电位随时间变化曲线如下：

ExpIF 模型的膜电位在动作电位发放过程中的极短时间内迅速上升，膜电位变化曲线异常陡峭，比QIF模型更真实。

3.2 各参数对ExpIF模型的影响

ExpIF模型相对LIF模型，两个独特的参数 $V_T,\Delta_T$ 均出现在指数项中。当V低于发放阈值 $V_T$ ，指数项可忽略，此时的的ExpIF模型与LIF模型等价。

由上图可得， $\Delta_T$ 越大，膜电位的变化越平缓。 $V_T$ 是指数项从缓慢上升向快速上升的转折点，其含义与LIF模型中的 $V_{th}$ 类似。测试 $\Delta_T$ 的取值对神经元膜电位变化曲线的影响：

duration=30

group1 = ExpIF(1,delta_T=0.02)
runner = bp.dyn.DSRunner(group1,monitors=['V'],inputs=('input',20),dt=0.01)
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$ΔT=0.02$')

group2 = ExpIF(1,delta_T=1.)
runner = bp.dyn.DSRunner(group2,monitors=['V'],inputs=('input',20),dt=0.01)
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$ΔT=1$')

group3 = ExpIF(1,delta_T=5.)
runner = bp.dyn.DSRunner(group3,monitors=['V'],inputs=('input',20),dt=0.01)
runner(duration)
plt.plot(runner.mon.ts,runner.mon.V,label=r'$ΔT=5$')

plt.xlabel('t(ms)')
plt.ylabel('V(mV)')
plt.legend()
plt.show()

输出图像如下：

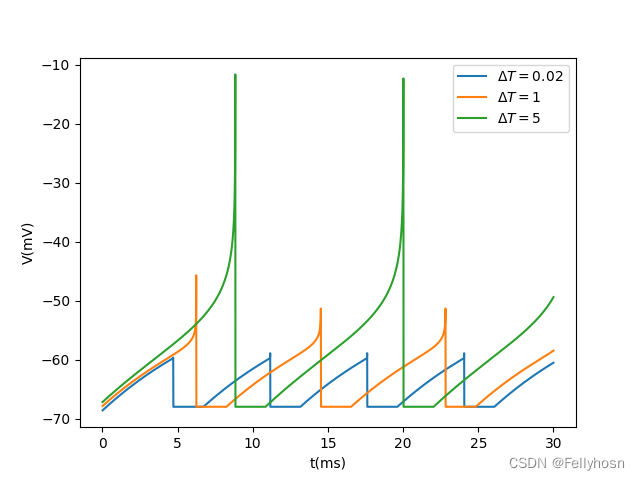
ExpIF模型与QIF模型最大的区别在于ExpIF神经元膜电位在越过兴奋阈值后急速上升，这和真实神经元的激发过程更加相似。事实上，研究发现一些神经元的生理数据可以很好地被 ExpIF 模型拟合，表明 ExpIF是一种很好的简化模型。

4 适应性指数整合发放（AdEx）模型

4.1 AdEx模型定义

QIF与ExpIF模型的缺陷在于：神经元对于膜电位变化没有记忆性！事实上，适应性是人类的智能表征之一，正是有了对之前刺激的“记忆”与适应，才使得我们在面对下一次相同或相似的刺激时能够做出更好的决策。例如：刚进入卫生间的一段时间和已经进入卫生间很长时间相比，后者感受到的刺激更少，这并不代表气味刺激的消失，而是我们对气味刺激的一种适应。

同样，单个神经元的行为也具有类似的特点：某些神经元面对外部的恒定刺激时，一开始高频发放，随后发放率逐渐降低，最终稳定在一个较小值，此之谓神经元的适应行为。适应行为使得神经元对新的刺激敏感而对持续重复的刺激脱敏，从而降低信息编码的能量损耗，提高编码效率。

基于这样的想法，Brette与Gerstner提出了适应性指数整合发放模型（AdEx），引入了适应变量w来描述神经元的适应性：

$\begin{matrix} \tau_m\frac{dV}{dt}=-(V-V_{rest})+\Delta_Te^\frac{V-V_T}{\Delta_T}-Rw+RI(t) \\ \tau_w\frac{dw}{dt}=a(V-V_{rest})-w+b\tau_w\displaystyle\sum_{t^{(f)}}\delta(t-t^{(f)}) \\ \text{if }V>\theta,\quad V\leftarrow V_{reset}\text{ last }t_{ref} \end{matrix}$

第一个方程右侧增加了一项-Rw表示膜电位还受到适应变量w的调节，w越大表示神经元的适应性越强。第二个方程刻画了w的变化，主要由三部分组成：第一项 $a(V-V_{rest})$ 表示膜电位V对w起正向调控，膜电位越高，神经元适应性增加越快；第二项-w为衰减项；第三项描述了动作电位对w的影响，其中 $t^{(f)}$ 表示神经元动作电位发放时刻，当 $t=t^{(f)}$ 时，w会瞬时增加b，代表神经元每产生一个动作电位，神经元的适应性便会增加一个固定值。

4.2 AdEx模型代码实现

用brainpy搭建AdEx模型：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class AdEx(bp.dyn.NeuGroup):
    def __init__(self,size,V_rest=-65.,V_reset=-68.,delta_T=1.,
                 V_th=20,V_T=-60,a=1.,b=2.5,R=1.,tau=10.,tau_w=30.,t_ref=0,name=None):
        super(AdEx,self).__init__(size=size,name=name)

        self.V_rest = V_rest
        self.V_reset = V_reset
        self.V_th = V_th
        self.V_T = V_T
        self.delta_T = delta_T
        self.a = a
        self.b = b
        self.tau_w = tau_w
        self.R = R
        self.tau = tau
        self.t_ref = t_ref

        self.V = bm.Variable(bm.random.randn(self.num) + V_reset)
        self.w = bm.Variable(bm.zeros(self.num))
        self.input = bm.Variable(bm.zeros(self.num))
        self.t_last_spike = bm.Variable(bm.ones(self.num)* -1e7) #上一次脉冲发放时刻
        self.refractory = bm.Variable(bm.zeros(self.num,dtype=bool)) #是否处于不应期
        self.spike = bm.Variable(bm.zeros(self.num,dtype=bool)) #脉冲发放状态

        self.integral = bp.odeint(f=self.derivative,method='exp_auto')

    def dV(self,V,t,w,Iext):
        tmp = self.delta_T * bm.exp((V - self.V_T) / self.delta_T)
        dVdt = (-V + self.V_rest + tmp - self.R * w + self.R * Iext) / self.tau
        return dVdt
    def dw(self,w,t,V):
        dwdt = (self.a * (V-self.V_rest)-w)/self.tau_w
        return dwdt
    @property
    def derivative(self):
        return bp.JointEq(self.dV,self.dw) #联合两个微分方程

    def update(self,tdi):
        t, dt = tdi.t, tdi.dt
        V,w = self.integral(self.V,self.w,t,self.input,dt=dt)
        refractory = (t - self.t_last_spike) <= self.t_ref  # 是否处于不应期
        V = bm.where(refractory, self.V, V)
        spike = V > self.V_th  # 更新脉冲状态
        self.spike.value = spike
        self.t_last_spike = bm.where(spike, t, self.t_last_spike)  # 更新上次脉冲时间
        self.V.value = bm.where(spike, self.V_reset, V)
        self.w.value = bm.where(spike,w+self.b,w)
        self.refractory.value = bm.logical_or(refractory, spike)
        self.input[:] = 0  # 重置外界输入
neu = AdEx(1)
runner = bp.dyn.DSRunner(neu,monitors=['V','w','spike'],inputs=('input',9.),dt=0.01)
runner(500)
#可视化V与w
runner.mon.V = np.where(runner.mon.spike,20.,runner.mon.V)
plt.plot(runner.mon.ts,runner.mon.V,label='V')
plt.plot(runner.mon.ts,runner.mon.w,label='w')
plt.xlabel('t(ms)')
plt.ylabel('V(mV)')
plt.show()

输出图像（给定相同的参数，膜电位初始值的微小变动使得 AdEx 模型出现了不同的模拟结果）：

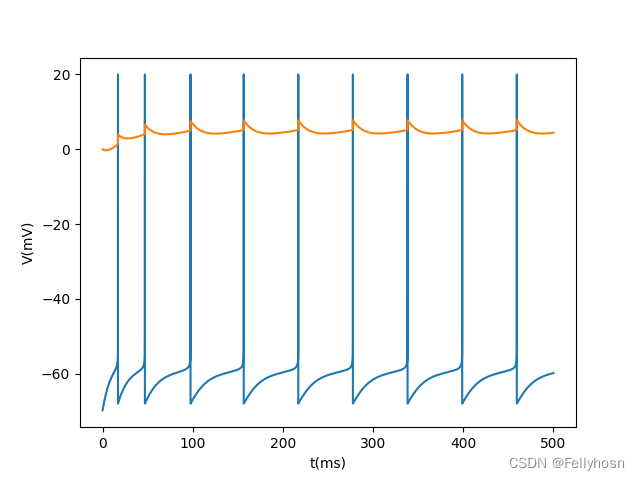
第一张图的神经元在恒定刺激下发放频率逐渐降低，最终趋于一个恒定值；第二张图的神经元发放频率降低，最终停止发放，不再兴奋。这是由于代码中膜电位的初始值是随机的，因此会对结果产生影响。AdEx模型不仅能模拟神经元的适应行为，还能模拟神经元的各种发放模式。

4.3 AdEx模型的发放模式

不同脑区、不同类型的神经元具有不同的发放模式。根据神经元在恒定刺激下产生动作电位的时间间隔的不同，可以将神经元的发放分为四种模式:

激发锋发放 (tonic spiking):也叫规律发放 (regular spiking)，动作电位之间的时间间隔相同
适应性发放 (adapting): 动作电位之间的时间间隔逐渐变大，最后趋于一个恒定值
簇发放(bursting):神经元在短时间内连续产生多个脉冲，然后在较长时间间隔内不再发放，并如此周期性重复
不规律发放 (irregular spiking): 动作电位之间的时间间隔不具有明显的规律。上述分类是基于神经元稳定发放的状态而决定的。

有的神经元在刚接受刺激时具有独特的发放模式，这是因为神经元的起始状态和接受刺激后的稳定状态差别较大，从起始状态转变为稳定状态需要一定时间。神经元起始阶段的发放模式又可以被分为三类:

典型发放(classic/tonic spiking):起始阶段和稳定阶段的发放没有差别
起始族发放 (initial burst): 起始阶段出现短时间的连续发放，发放频率远高于稳定状态
延迟发放 (delayed spiking): 神经元在经过一段较长时间的下变化后才开始发放。

理论上，神经元起始状态的分类和稳定状态的分类可以两两组合，形成 12 种发放模式。所有发放模式的组合都能在电生理实验中被观察到。有趣的是，这些发放模式都能够被 AdEx 模型重现。其对应参数如下：

可以通过相平面分析法来研究不同发放模式的动力学机制。

5 Izhikevich模型

5.1 Izhikevich模型的定义

AdEx模型是在ExpIF模型上增加了适应变量，使得模型具有多样的动力学表征能力。同理，可以在QIF模型的基础上增加适应变量，增加原有模型的表征能力。这就是Izhikevich在2003年提出的Izhikevich模型，其表达式如下：

$\begin{matrix} \frac{dV}{dt}=0.04V^2+5V+140-u+I \\ \frac{du}{dt}=a(bV-u) \\ \text{if }V>\theta,\quad V\leftarrow c,u\leftarrow u+d \text{ last } t_{ref} \end{matrix}$

与QIF模型相比，Izhikevich模型的第一个式子右边为关于V的展开后的二次方程，其各项系数是通过拟合一个皮层神经元得到的，也可以根据不同拟合情况改变。模型的第二个式子中，u被称为膜电位恢复变量，它的作用和AdEx模型中的适应变量w相同。

5.2 Izhikevich模型的代码实现

用brainpy搭建Izhikevich模型：

import brainpy as bp
import brainpy.math as bm
import numpy as np
import matplotlib.pyplot as plt

class Izhikevich(bp.dyn.NeuGroup):
    def __init__(self,size,a=0.02,b=0.20,c=-65.,d=2.,V_th=30.,t_ref=0.,name=None):
        super(Izhikevich,self).__init__(size=size,name=name)

        self.a = a
        self.b = b
        self.c = c
        self.d = d
        self.V_th =V_th
        self.t_ref = t_ref

        self.V = bm.Variable(bm.random.randn(self.num) - 65.)
        self.u = bm.Variable(self.V * b)
        self.input = bm.Variable(bm.zeros(self.num))
        self.t_last_spike = bm.Variable(bm.ones(self.num)* -1e7) #上一次脉冲发放时刻
        self.refractory = bm.Variable(bm.zeros(self.num,dtype=bool)) #是否处于不应期
        self.spike = bm.Variable(bm.zeros(self.num,dtype=bool)) #脉冲发放状态

        self.integral = bp.odeint(f=self.derivative,method='exp_auto')

    def dV(self,V,t,u,Iext):
        return 0.04*V*V+5*V+140-u+Iext
    def du(self,u,t,V):
        return self.a*(self.b*V-u)

    @property
    def derivative(self):
        return bp.JointEq([self.dV,self.du]) #联合两个微分方程

    def update(self,tdi):
        t, dt = tdi.t, tdi.dt
        V,u = self.integral(self.V,self.u,t,self.input,dt=dt)
        refractory = (t - self.t_last_spike) <= self.t_ref  # 是否处于不应期
        V = bm.where(refractory, self.V, V)
        spike = V > self.V_th  # 更新脉冲状态
        self.spike.value = spike
        self.t_last_spike = bm.where(spike, t, self.t_last_spike)  # 更新上次脉冲时间
        self.V.value = bm.where(spike, self.c, V)
        self.u.value = bm.where(spike,u+self.d,u)
        self.refractory.value = bm.logical_or(refractory, spike)
        self.input[:] = 0  # 重置外界输入

在不同的参数设置下，Izhikevich模型具有多种发放模式。可用分岔分析法进行研究。