MADA-Learning to Learn Single Domain Generalization阅读记录

方法

目标是解决单域泛化问题：模型仅在一个源域$S$中训练，但要求在许多未见过的目标域$T$上泛化良好。受到许多最近成就的启发[36,56,24]，这个具有挑战性的问题的一个有希望的解决方案是利用对抗训练[11,49]。关键思想是学习一个抗分布外扰动的鲁棒模型。更具体地说，我们可以通过解决最坏情况问题来学习模型[44]:
$$\underset{\theta }{\min }\underset{\mathcal{T}:D(\mathcal{S},\mathcal{T})\le \rho }{\sup }\mathbb{E}[{\mathcal{L}}_{\mathrm{task}}(\theta ;\mathcal{T})],（1）$$其中$D$是测量域距离的相似性度量，$\rho$表示$S$和$T$之间的最大域差异。θ是根据任务特定目标函数$L_{task}$优化的模型参数。理解：(${\min }_{\theta }$) 表示我们要最小化的是关于参数 ($\theta$) 的某个函数。(${\sup }_{\mathcal{T}:D(\mathcal{S},\mathcal{T})\le \rho }$) 表示在所有满足某个条件的训练集 ($\mathcal{T}$) 上取最大值。这里的($D(\mathcal{S},\mathcal{T})$) 表示两个数据分布之间的距离，而 ($\rho$) 是一个给定的阈值。($\mathbb{E}[{\mathcal{L}}_{\mathrm{task}}(\theta ;\mathcal{T})]$) 表示在训练集 ($\mathcal{T}$) 上关于参数 ($\theta$) 的某个损失函数的期望值。总的来说这个公式的意义是：要找到能够最小化在所有满足某种数据分布距离约束条件下的训练集上的某个损失函数的期望值的参数 ($\theta$)。这种形式的优化问题在对抗性训练或者用于泛化保证时可能会经常出现。在这里，我们关注使用交叉熵损失的分类问题:
$${\mathcal{L}}_{\mathrm{task}}(\mathbf{y},\hat{\mathbf{y}})=-\sum _i{y}_i\log ({\hat{y}}_i),（2）$$其中$\hat{\mathbf{y}}$为模型的softmax输出;$\mathbf{y}$是表示真类的one-hot向量;$y_i$和${\hat{y}}_i$分别表示$y$和$\hat{y}$的第$i$维。

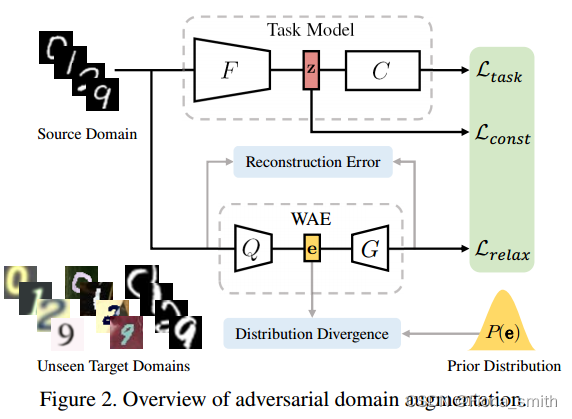
根据最坏情况公式（1），我们提出了一种新的方法，基于元学习的对抗域增强(M-ADA)，用于单域泛化。图2概述了我们的方法。在第3.1节中，我们通过利用对抗性训练来增强源域，创建了“虚构”但“具有挑战性”的域。在Wasserstein自动编码器(WAE)的帮助下，任务模型从域增强中学习，这放宽了第3.2节中的最坏情况约束。我们在如3.3节所述的学会学习的框架下组织任务模型和WAE的联合训练，以及领域增强过程。最后，在第四节给出了最坏情况保证的理论证明。

对抗性域增强

我们的目标是从源域创建读个增强域。增强域要求与源域在分布上不同，以模拟不可见的域。此外，为避免增强域发散，还应满足式(1)中定义的最坏情况保证。为了实现这一目标，我们提出了对抗性域增强。
为了实现这一目标，我们提出了对抗性域增强。我们的模型由任务模型和WAE组成，如图2所示。在图2中，任务模型由特征提取器$F:X\to Z$映射图像从输入空间到嵌入空间，和一个分类器$C:Z\to Y$用于从嵌入空间预测标签。设$z$表示由$z=F(x)$得到的$x$的潜在表示。总体损失函数的表达式为：
$${\mathcal{L}}_{\mathrm{ADA}}=\underset{\text{Classification}}{\underbrace{{\mathcal{L}}_{\mathrm{task}}(\theta ;\mathbf{x})}}-\alpha \underset{\text{Constraint}}{\underbrace{{\mathcal{L}}_{\mathrm{const}}(\theta ;\mathbf{z})}}+\beta \underset{\text{Relaxation}}{\underbrace{{\mathcal{L}}_{\mathrm{relax}}(\psi ;\mathbf{x})}},(3)$$其中${\mathcal{L}}_{\mathrm{task}}$为Eq.(2)中定义的分类损失，${\mathcal{L}}_{\mathrm{const}}$为Eq.(1)中定义的最坏情况保证，${\mathcal{L}}_{\mathrm{relax}}$为Eq.(7)中定义的大域传输保证，$\psi$为WAE参数。$\alpha$和$\beta$是平衡${\mathcal{L}}_{\mathrm{const}}$和${\mathcal{L}}_{\mathrm{relax}}$的两个超参数。
给定目标函数${\mathcal{L}}_{\mathrm{ADA}}$，我们采用迭代方法在增强域$S^{+}$中生成对抗样本$x^{+}$:
$${\mathbf{x}}_{t+1}^{+}\leftarrow {\mathbf{x}}_t^{+}+\gamma {\nabla }_{{\mathbf{x}}_t^{+}}{\mathcal{L}}_{\mathrm{ADA}}(\theta ,\psi ;{\mathbf{x}}_t^{+},{\mathbf{z}}_t^{+}),(4)$$式中，$\gamma$为梯度上升的学习率。需要少量的迭代来产生足够的扰动并创建理想的对抗样本。
${\mathcal{L}}_{\mathrm{const}}$对对抗样本施加语义一致性约束，使得$S^{+}$满足$D(S;S^{+})\le \rho$。特别地，我们根据[56]测量嵌入空间中$S^{+}$与$S$之间的Wasserstein距离:
$${\mathcal{L}}_{\mathrm{const}}=\frac{1}{2}\Vert \mathbf{z}-{\mathbf{z}}^{+}{\Vert }_2^2+\infty \cdot 1\left\{\mathbf{y}\ne {\mathbf{y}}^{+}\right\},(5)$$其中 1 { ⋅ } 1\{·\} 1{⋅}为0-1指示函数，如果$x^{+}$的类标号不同于$x$，则${\mathcal{L}}_{\mathrm{const}}$为1。直观上，${\mathcal{L}}_{\mathrm{const}}$控制着以Wasserstein距离度量的源域外的泛化能力[54]。然而，${\mathcal{L}}_{\mathrm{const}}$产生有限的域迁移，因为它严重限制了样本和它们的扰动之间的语义距离。因此，提出${\mathcal{L}}_{\mathrm{relax}}$来放松语义一致性约束，创建大域传输。${\mathcal{L}}_{\mathrm{relax}}$的实现将在第3.2节中讨论。

Wasserstein距离约束的松弛

直观地说，我们期望增强域$S^{+}$与源域$S$有很大的不同。换句话说，我们希望最大化$S^{+}$与$S$之间的域差异。然而，语义一致性约束${\mathcal{L}}_{\mathrm{const}}$将严重限制从$S$到$$S^{+}$的域传输，这对生成理想的$S^{+}$提出了新的挑战。为了解决这个问题，我们使用${\mathcal{L}}_{\mathrm{relax}}$来鼓励分布外域扩展。我们在图3中说明了这个想法。

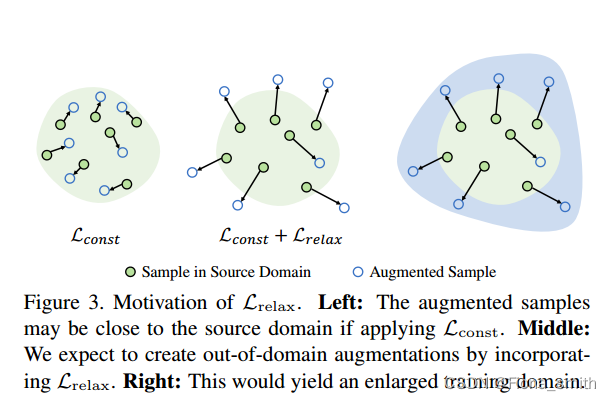
具体来说，我们使用Wasserstein自动编码器(WAEs)[52]来实现${\mathcal{L}}_{\mathrm{relax}}$。设$V$表示$\psi$参数化的WAE。$V$由编码器$Q(e|x)$和解码器$G(x|e)$组成，其中$x$和$e$分别表示输入和瓶颈嵌入。此外，我们使用距离度量$D_e$来测量$Q(x)$与先验分布$P(e)$之间的散度，这可以实现为最大平均差异(MMD)或GAN[10]。我们可以通过优化来学习$V$：

$$\underset{\psi }{\min }[\Vert G(Q(\mathbf{x}))-\mathbf{x}{\Vert }^2+\lambda {\mathcal{D}}_{\mathbf{e}}(Q(\mathbf{x}),P(\mathbf{e}))],(6)$$其中$\lambda$是超参数。在源域$S$上离线预训练$V$后，我们将其冻结并最大化域增强重建误差${\mathcal{L}}_{\mathrm{relax}}$:
$${\mathcal{L}}_{\mathrm{relax}}=\Vert {\mathbf{x}}^{+}-V({\mathbf{x}}^{+}){\Vert }^2.(7)$$与Vanilla或Variation Auto-Encoders不同[45]，WAEs使用Wasserstein度量来度量输入和重建之间的分布距离。因此，预训练的$V$可以更好地捕获源域的分布，最大化${\mathcal{L}}_{\mathrm{relax}}$会产生大的域传输。在附录中还提供了不同${\mathcal{L}}_{\mathrm{relax}}$的比较。
在这项工作中，$V$作为一个one-class鉴别器来区分增强是否在源域之外，这与传统gan的鉴别器有很大的不同[10]。它也不同于领域自适应中广泛使用的领域分类器[24]，因为只有一个源领域可用。因此，使用${\mathcal{L}}_{\mathrm{relax}}$和${\mathcal{L}}_{\mathrm{const}}$一起在输入空间“推走”$S^{+}$，同时在嵌入空间“拉回”$S^{+}$。在第4节中，我们展示了${\mathcal{L}}_{\mathrm{relax}}$和${\mathcal{L}}_{\mathrm{const}}$分别是在输入空间和嵌入空间中定义的两个Wasserstein距离度量的派生。

元学习单域泛化

为了有效地组织源域$S$和增强域$S^{+}$上的模型训练，我们利用元学习方案来训练单个模型。为了模拟源域$S$和目标域$T$之间的真实域位移，在每次学习迭代中，我们对源域$S$进行元训练，并对所有增强域$S^{+}$进行元测试。因此，在多次迭代之后，该模型在评估过程中有望在最终目标域$T$上实现良好的泛化。
正式地，提出的基于元学习的对抗领域增强(M-ADA)方法在训练过程中的每次迭代中由三个部分组成:元训练、元测试和元更新。在元训练中，${\mathcal{L}}_{\mathrm{task}}$在源域$S$的样本上计算，模型参数$\theta$通过一个或多个梯度步更新，学习率为$\eta$:$$\hat{\theta }\leftarrow \theta -\eta {\nabla }_{\theta }{\mathcal{L}}_{\mathrm{task}}(\theta ;\mathcal{S}).(8)$$然后计算${\mathcal{L}}_{\mathrm{task}}(\hat{\theta };\mathcal{S}+k)$在元测试中每个增强域$S+k$上。最后，在meta-update中，我们通过同时优化meta-train和meta-test的组合损失计算的梯度来更新$\theta$:
$$\theta \leftarrow \theta -\eta {\nabla }_{\theta }[{\mathcal{L}}_{\mathrm{task}}(\theta ;\mathcal{S})+\sum _{k=1}^K{\mathcal{L}}_{\mathrm{task}}(\hat{\theta };{\mathcal{S}}_k^{+})],(9)$$$K$是增广域的个数

整个训练流程如表1所示。我们的方法有以下优点。首先，与之前学习一系列集成模型的工作[56]相比，我们的方法实现了单个模型的效率。在第5.4节中，我们证明M-ADA在内存、速度和准确性方面略微优于[56]。其次，元学习方案为学习模型的快速适应做好准备:一个或少量的梯度步骤将在新的目标域上产生改进的行为。这使M-ADA能够进行第5.5节所示的少量域适应。

理论的理解

我们提供了一个详细的理论分析所提出的对抗域增强。具体地说，我们证明了Eq.(3)中定义的整体损失函数是一个松弛的最坏情况问题的直接推导。
让 c : Z × Z → R + ∪ { ∞ } c : \mathcal{Z}\times\mathcal{Z} \to \mathbb{R}_{+} \cup \{\infty\} c:Z×Z→R+​∪{∞}为对手在嵌入空间中将$z$扰动到$z^{+}$的“代价”。让 d : X × X → R + ∪ { ∞ } d : \mathcal{X} \times \mathcal{X} \to \mathbb{R}_{+} \cup \{\infty\} d:X×X→R+​∪{∞}是对手在输入空间中将$x$扰动为$x^{+}$的“代价”。$S$和$S^{+}$之间的Wasserstein距离可以表示为:$W_c(\mathcal{S},{\mathcal{S}}^{+}):={\inf }_{M_{\mathbf{z}}\in \Pi (\mathcal{S},{\mathcal{S}}^{+})}{\mathbb{E}}_{M_{\mathbf{z}}}\left[c\left(\mathbf{z},{\mathbf{z}}^{+}\right)\right]$和$W_d(\mathcal{S},{\mathcal{S}}^{+}):={\inf }_{M_{\mathbf{x}}\in \Pi (\mathcal{S},{\mathcal{S}}^{+})}{\mathbb{E}}_{M_{\mathbf{x}}}\left[d\left(\mathbf{x},{\mathbf{x}}^{+}\right)\right]$，其中$M_z$和$M_x$分别是嵌入空间和输入空间的测度;$\Pi (\mathcal{S},{\mathcal{S}}^{+})$是$S$和$S^{+}$的联合分布。则松弛最坏情况问题可表示为:
$${\theta }^{\ast }=\underset{\theta }{\min }\underset{{\mathcal{S}}^{+}\in \mathcal{D}}{\sup }\mathbb{E}[{\mathcal{L}}_{\mathrm{task}}(\theta ;{\mathcal{S}}^{+})],(10)$$
式中 D = { S + : W c ( S , S + ) ≤ ρ , W d ( S , S + ) ≥ η } \mathcal{D}=\{\mathcal{S}^{+}:W_{c}(\mathcal{S},\mathcal{S}^{+})\leq\rho,W_{d}(\mathcal{S},\mathcal{S}^{+})\geq\eta\} D={S+:Wc​(S,S+)≤ρ,Wd​(S,S+)≥η}。我们注意到，在Wasserstein距离测度$W_c$和$W_d$下，$D$覆盖了一个鲁棒区域，该区域在嵌入空间中距离$S$的$\rho$距离内，在输入空间中距离$S$的$\eta$距离内。
对于深度神经网络，Eq.(10)是难以处理的任意$\rho$和$\eta$。因此，我们考虑其定罚参数$\alpha \ge 0$和$\beta \ge 0$时的拉格朗日松弛:
min ⁡ θ { sup ⁡ S + { E [ L t a s k ( θ ; x + ) ] − W c , d } = E [ ϕ α , β ( θ , ψ ; x ) ] } , \min_\theta\{\sup_{\mathcal{S}^+}\left\{\mathbb{E}[\mathcal{L}_{\mathrm{task}}(\theta;\mathbf{x}^+)]-W_{c,d}\right\}=\mathbb{E}[\phi_{\alpha,\beta}(\theta,\psi;\mathbf{x})]\}, θmin​{S+sup​{E[Ltask​(θ;x+)]−Wc,d​}=E[ϕα,β​(θ,ψ;x)]},
我们有 W c , d ( S , S + ) = α W c ( S , S + ) − β W d ( S , S + ) , ϕ α , β ( θ , ψ ; x ) = sup ⁡ x + { L t a s k ( θ ; x + ) − L c , d } W_{c,d}(\mathcal{S},\mathcal{S}^{+})=\alpha W_{c}(\mathcal{S},\mathcal{S}^{+})-\beta W_{d}(\mathcal{S},\mathcal{S}^{+}),\phi_{\alpha,\beta}(\theta,\psi;\mathbf{x})=\sup_{\mathbf{x}^{+}}\{\mathcal{L}_{\mathrm{task}}(\theta;\mathbf{x}^{+})-\mathcal{L}_{c,d}\} Wc,d​(S,S+)=αWc​(S,S+)−βWd​(S,S+),ϕα,β​(θ,ψ;x)=supx+​{Ltask​(θ;x+)−Lc,d​}和${\mathcal{L}}_{c,d}=\alpha c(\mathbf{z},{\mathbf{z}}^{+})-\beta d(\mathbf{x},{\mathbf{x}}^{+})$。因此，将Eq.(10)中的问题转化为最小化稳健代理${\varphi }_{\alpha ,\beta }$。
根据[44]，${\varphi }_{\alpha }$关于$\theta$是光滑的，如果$\alpha$足够大，且Lipschitzian光滑假设成立，则${\varphi }_{\alpha }$是光滑的。由于$\psi$和$\theta$相互独立，${\varphi }_{\alpha ,\beta }$仍然关于$\theta$是光滑的。梯度可以计算为:
$${\nabla }_{\theta }{\varphi }_{\alpha ,\beta }(\theta ,\psi ;\mathbf{x})={\nabla }_{\theta }{\mathcal{L}}_{\mathrm{task}}(\theta ;{\mathbf{x}}^{\star }(\mathbf{x},\theta ,\psi )),$$
其中${\mathbf{x}}^{\star }(\mathbf{x},\theta ,\psi )=\arg {\max }_{{\mathbf{x}}^{+}}[{\mathcal{L}}_{\mathrm{task}}(\theta ;{\mathbf{x}}^{+})-{\mathcal{L}}_{c,d}]=\arg {\max }_{{\mathbf{x}}^{+}}{\mathcal{L}}_{\mathrm{ADA}}(\theta ,\psi ;{\mathbf{x}}^{+},{\mathbf{z}}^{+})$
，即公式(3)中定义的对抗性扰动。