Hierarchical Clustering
层次聚类试图在不同的层次上对数据集进行划分,从而形成树形的聚类结构。层次聚类一般可以分为如下两类:
自底向上
最开始时每个样本都是一个单独的簇,然后在每一次迭代中合并两个距离最近的簇为一个簇,不断进行此类操作,直到簇的个数到达预先设定的值。其中代表性的算法便是AGNES(AGglomera tive NESting),算法流程如下所示:
输入:包含n个样本的数据集,终止条件簇的数目k 输出:k个簇
将每个样本当成一个初始簇 Repeat
根据两个簇中最近的数据点找到最近的两个簇
合并两个簇,生成新的簇的集合
Until 达到定义的簇的数目
AGNES算法中最关键的问题是簇之间的距离度量,因为簇是样本的集合,所以簇之间距离的度量可以转化为样本之间距离的度量。假设有两个簇 C i C_{i} Ci和 C j C_{j} Cj,可以定义如下的几种距离:
- 最小距离: d min ( C i , C j ) = min p ⊂ C i , q ∈ C j ∣ p − q ∣ d_{\min }\left(C_{i}, C_{j}\right)=\min _{p \subset C_{i}, q \in C_{j}}|p-q| dmin(Ci,Cj)=minp⊂Ci,q∈Cj∣p−q∣,对应的为单连接算法,如果两个最近的簇之间的距离超过了用户给定的阈值时,聚类结束;
- 最大距离: d max ( C i , C j ) = max p ∈ C i , q ∈ C j ∣ p − q ∣ d_{\max }\left(C_{i}, C_{j}\right)=\max _{p \in C_{i, q} \in C_{j}}|p-q| dmax(Ci,Cj)=maxp∈Ci,q∈Cj∣p−q∣,对应的为全连接算法,如果两个簇之间的最大距离超过了用户给定的阈值时,聚类结束;
- 均值距离: d mean ( C i , C j ) = ∣ p ‾ − q ‾ ∣ , # ∓ p ‾ = 1 ∣ C i ∣ ∑ p ∈ C i p , q ‾ = 1 ∣ C j ∣ ∑ q ∈ C j q d_{\text {mean}}\left(C_{i}, C_{j}\right)=|\overline{p}-\overline{q}|, \# \mp \overline{p}=\frac{1}{\left|C_{i}\right|} \sum_{p \in C_{i}} p, \overline{q}=\frac{1}{\left|C_{j}\right|} \sum_{q \in C_{j}} q dmean(Ci,Cj)=∣p−q∣,#∓p=∣Ci∣1∑p∈Cip,q=∣Cj∣1∑q∈Cjq,其中 p ‾ \overline{p} p和 q ‾ \overline{q} q为簇的均值中心
- 平均距离:
d
a
v
g
(
C
i
,
C
j
)
=
1
∣
C
i
∣
∣
C
j
∣
∑
p
∈
C
i
q
c
C
j
∣
p
−
q
∣
d_{a v g}\left(C_{i}, C_{j}\right)=\frac{1}{\left|C_{i}\right|\left|C_{j}\right|} \sum_{p \in C_{i} q c C_{j}}|p-q|
davg(Ci,Cj)=∣Ci∣∣Cj∣1∑p∈CiqcCj∣p−q∣

下面给出一个形象化的小栗子
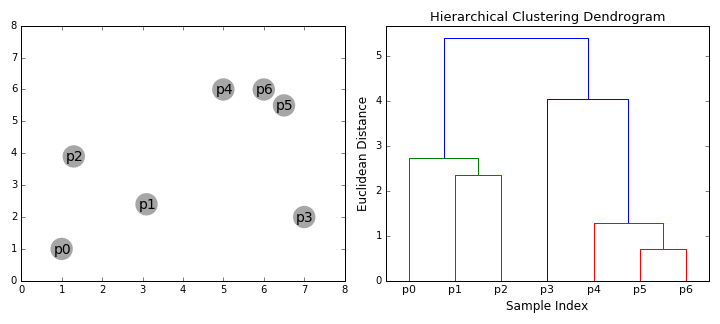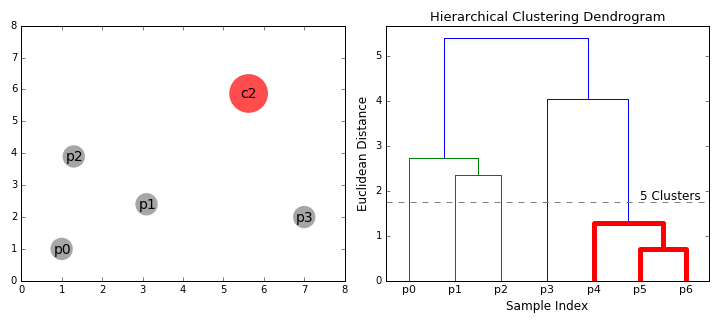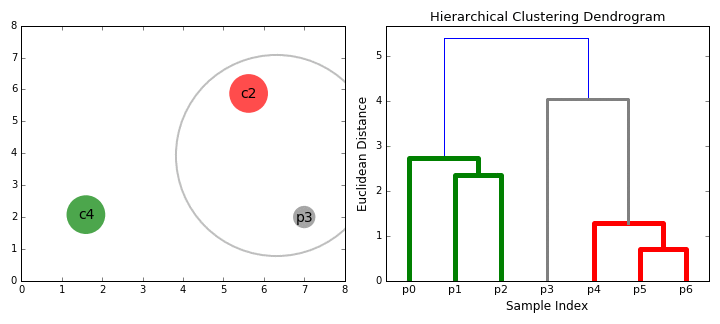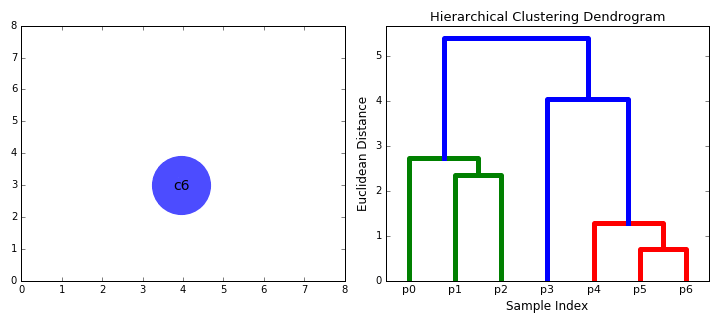
自顶向下
开始时将所有的样本看作一个簇,然后不断的分裂,直到簇的个数到达预先设定的值。其中,BIRCH算法便是其中最著名的一个,它的全称为利用层次方法的平衡迭代规约和聚类(Balanced Iterative Reducing and Clustering Using Hierarchies),使用层次方法来聚类和规约数据,使用聚类特征树(CF树)来表示聚类的层次结构。而且只需要扫描一遍数据库就能进行聚类,时间开销小,适合于数据集较大的情形。
在CF树中,每一个聚类特征使用一个三元组表示: C F = < n , L S , S S > CF=<n,LS,SS> CF=<n,LS,SS>:
- n:CF中拥有的样本的数量
- LS:CF中拥有的样本个特征维度的向量
- SS:CF中拥有的样本各特征维度的平方和

使用这样的结构有如下的诸多优点:
- 可以推导出簇的许多有用的统计量
- 只需固定大小的空间来存储聚类特征
- 聚类特征满足线性可加性
BIRCH主要包括两个阶段:
- 阶段一:扫描数据库,建立一棵存放于内存的初始CF树,
- 阶段二:采用某个其它的聚类算法对CF树的叶节点进行聚类,比如典型的划分方法
下面通过一个例子看一下如何构建CF树。首先放入第一个样本,此时样本数量为1,CF树的根节点也为A

然后继续放入下一个样本,因为此时它和第一个样本点都在半径为 T T T的超球体中,所以它们位于同一个簇,CF树的形状不发生变化,只需更新 n = 2 n=2 n=2

接着继续放入第三个样本,发现它不在位于以第一个样本点为中心、半径为 T T T的超球体中,所以需要新建一个三元组存储它的信息,此时CF结构发生改变,拥有两个节点

接着放入第四个样本点的时候,我们发现和B在半径小于T的超球体,所以它和B位于同一个簇中,CF树的整体结构不变

假设我们规定叶子节点中最大的CF数为3,那么目前CF树的情况如下所示,其中 L N 1 LN1 LN1中有3个CF,已满足最大数量限制, L N 2 、 L N 3 LN2、LN3 LN2、LN3各有两个。如果此时来了一个样本 s c 8 sc8 sc8,它恰好位于 L N 1 LN1 LN1的超球体中,但是 L N 1 LN1 LN1中已经有了 s c 1 、 s c 2 、 s c 3 sc1、sc2、sc3 sc1、sc2、sc3,无法继续添加

此时唯一的办法就是分裂 L N 1 LN1 LN1,将 s c 8 sc8 sc8和较近的 s c 1 sc1 sc1放入同一个叶子节点,另外两个放入另一个叶子节点,这样 L N 1 LN1 LN1就分裂为 L N 1 ′ LN1' LN1′和 L N 1 ′ ′ LN1'' LN1′′两个叶子节点。

但是在将LN1分裂为两个叶子节点后,根节点此时有4个叶子节点,如果同样的要求根节点拥有的最大CF数为3的话,也需要将根节点进行分裂

优点:
- 节约内存,所有的样本都在磁盘上,CF-树仅仅存了CF节点和对应的指针。
- 聚类速度快,只需要一遍扫描训练集就可以建立CF-树,CF-树增删改都很快
- 可以识别噪声点,还可以对数据集进行初步分类的预处理
缺点:
- 由于CF-树对每个节点的CF个数有限制,导致聚类的结果可能和真实的类别分布不同
- 如果数据集的分布簇不是类似于超球体,则聚类效果不好
详细介绍可见:
sklearn中根据不同的链接方式可使用不同参数设置的凝聚式聚类算法,算法对应的实现类为sklearn.cluster.AgglomerativeClustering,类相关的参数主要有:
- n_clusters:默认为2,即是否指定聚类后簇的个数,但当idstance_threshold不为None时该参数则必须为None
- affinity:定义相似度度量方式,默认为欧氏距离(euclidean),此外还可选l1、l2、manhattan、consine或是precomputed
- linkage:指指定具体的连接方式,可选“ward”, “complete”, “average”, “single”,默认为ward
- distance_threshold:指定簇在凝聚过程中连接距离的阈值
- …
API使用样例:
from sklearn.cluster import AgglomerativeClustering
for linkage in ('ward', 'average', 'complete', 'single'):
clustering = AgglomerativeClustering(linkage=linkage, n_clusters=10)
t0 = time()
clustering.fit(X_red)
print("%s :\t%.2fs" % (linkage, time() - t0))
plot_clustering(X_red, clustering.labels_, "%s linkage" % linkage)
详情可见:Various Agglomerative Clustering on a 2D embedding of digits
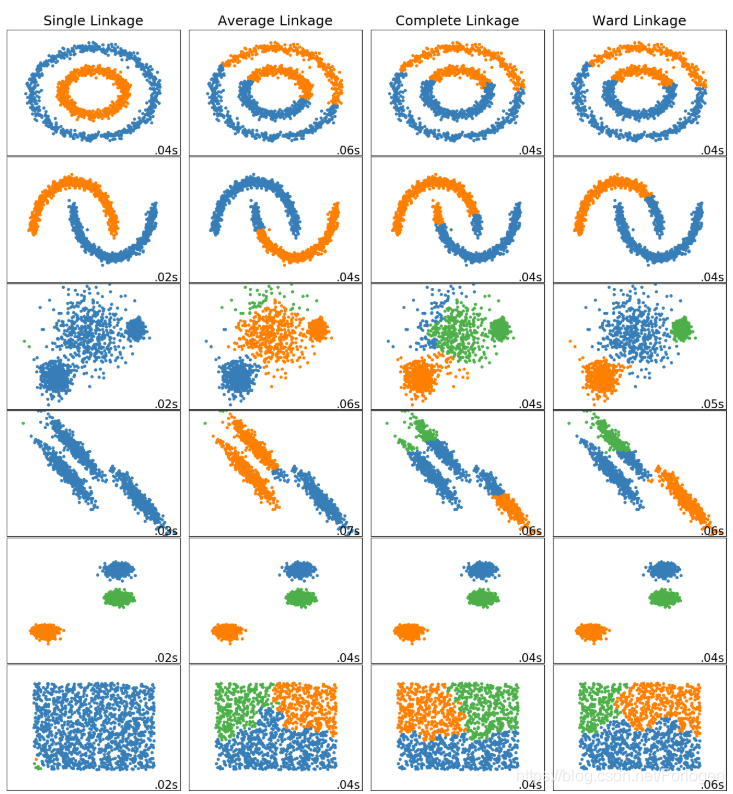
Comparing different hierarchical linkage methods on toy datasets
实验结果:
























 1762
1762

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








